II. Квадратичная зависимость скорости воспроизводства

от численности популяции N (члены популяции заинтересованы в ее росте - определяется частотой встреч особей различного пола, такая зависимость характерна также для некоторых химических реакций), смертность, как и ранее, считается пропорциональной N: a(N) = a₀(N), β(N) = β₀ = const. Модель имеет вид:

dN / dt = а N² - β N. (2)

Нелинейность уравнения порождает различные возможные режимы изменения численности со временем. Рассмотрим поведение функции N (t) при различных начальных численностях N(t=0) = N₀.

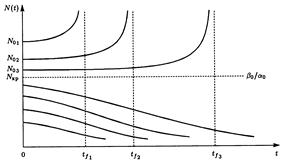а). a₀ = β₀, N₀ = N_кр. При равновесном (критическом) значении N₀, численность популяции не зависит от времени. Режим неустойчив – прим малых отклонениях от равновесного состояния решение удаляется от N_кр.

б). a₀ < β₀, N₀ < N_кр. Численность монотонно уменьшается со временем, стремясь к нулю при t → ∞.

в). a₀ > β₀, N₀ > N_кр. При начальном значении N₀ большем критического N_кр, рост численности носит взрывной характер (скорость воспроизводства имеет квадратичную зависимость). Численность растет со временем, причем настолько быстро, что обращается в бесконечность за конечное время t = t_f, тем меньшее, чем больше N₀.

Это свойство не частный результат, а имеет место для любых моделей вида

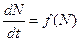, t > 0, N (0) > 0, f (N) > 0,

если при больших N функция f (N) растет быстрее первой степени.

III. Квадратичная зависимость смертности от численности популяции N - учет ограниченности доступных ресурсов (внутренняя конкуренция популяции - любая экологическая ниша может обеспечить существование популяции только до определенных пределов). Модель имеет вид:

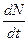= f (N) = aN + β N². (3)

Полагая, что N = N₀ при t=t₀, из последнего уравнения находим, что

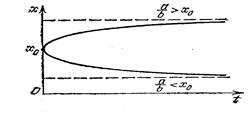
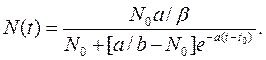
Отсюда видно, что при t → ∞ число особей в популяции N (t) →a/b. При этом возможны два случая: a/b > x₀ и a/b < N₀. Различия между этими двумя случаями видно из рисунка.

Приведенное соотношение описывает, в частности, популяции фруктовых вредителей и некоторых видов бактерий.

IV. «Равновесная» численность популяции N_р, которую может обеспечить окружающая среда

Скорость изменения численности пропорциональна самой численности, умноженной (в отличие от модели Мальтуса) на величину ее отклонения от равновесного значения:

dN / dt = k(1 – N / N_р) N, k>0. (4)

Или = kdt. Интегрируем ln (N_р – N) + lnN = kt + C.

Постоянная интегрирования определяется из условия N(t=0) = N₀, т.е. C = ln ((N_р – N)^-1 N₀).

Тогда N = N_р 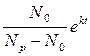- N 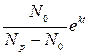или N(t) =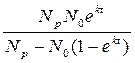

Член (1 – N/ N_р) обеспечивает механизм насыщения численности.

При N < N_р скорость роста положительна; N > N_р скорость роста отрицательна;

N → N_р скорость роста стремится к нулю.

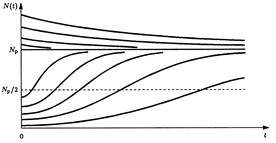Логистическая кривая – при любом N₀ численность стремится к равновесному значению тем медленнее, чем величина N (t) ближе к N₀. Равновесие устойчиво и более реалистично отражает динамику популяции.

Примем, что популяция может существовать только до определенного предела N_max и коэффициент прироста снижается по мере приближения к N_max. Численность популяции может измеряться в относительных единицах P = N/ N_max. Тогда функция прироста f (P) = r (1 - P).

Математическая постановка задачи.

Найти решение задачи Коши dР/dt = r(1 – Р)Р, где r – коэффициент прироста

при начальных условиях P(0) = P₀. В результате приходим к решению такого же вида, что и в предыдущей задаче.

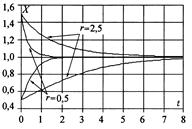
Р(t) = 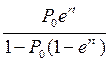На рисунке показано изменение относительной численности популяции во времени при различных начальных значениях P₀ и r. С течением времени величина Р → 1.

Проведем качественный анализ задачи. Найдем положение равновесия Р* (стационарную точку) для дифференциального уравнения dР/dt = r(1 – Р)Р, приравняв правую часть нулю. Получим две точки равновесия Р₁* = 0 и Р₂* = 1.

Ответ на вопрос, при каких условиях функция Р(t) останется близкой Р*, дает теорема Ляпунова об устойчивости по первому приближению.

Анализ устойчивости решения (устойчивость по Ляпунову) показывает следующее.

Положение равновесия Р₁* = 0 устойчиво при r < 0 (популяция является вымирающей).

Положение равновесия Р₂* = 1 устойчиво при r > 0.

При неизменных внешних условиях система быстро переходит в одно из устойчивых состояний равновесия и находится в нем до изменения внешних условий.

Определяющую роль в оценке развития популяции играет величина коэффициента прироста. Коэффициент прироста зависит от множества факторов, действующих как краткосрочно (стихийные бедствия), так и длительно (изменение климата). Степень влияния этих факторов на развитие популяции в большой мере зависит от величины популяции (для малых популяций изменение внешних условий может привести к существенной неустойчивости – вероятность вымирания выше).

Предположение о механизмах насыщения используются в моделях в различных областях.

Дата добавления: 2014-08-04; просмотров: 605; Нарушение авторских прав

Мы поможем в написании ваших работ!