Исследования модели и решение задачи

Интегрируя (2) получаем, что масса делящегося вещества убывает по экспоненциальному закону

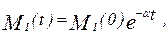
и при t → ∞ в области I вещество полностью исчезает.

Так как суммарная масса в соответствии с (1) остается постоянной, то в области II, количество вещества растет:

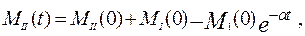
и при t → ∞ продукты распада полностью переходят из области I в область II.

Несмотря на физическое различие на простейшем уровне просматривается аналогия между радиоактивным распадом и динамикой популяций, в частности, изменение численности населения планеты, о чем свидетельствует одна из простейших моделей популяции, называемая моделью Мальтуса. В ее основу положено утверждение – скорость роста какой-либо величины пропорциональна текущему значению этой величины.

I. Скорость роста пропорциональна текущей величине населения N (t), умноженной на сумму коэффициентов рождаемости а (t) ≥ 0 и смертности β (t)≤ 0. В результате приходим к уравнению

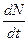= f (N) = dN (t) / dt = [а (t) - β (t)] N (t), a > 0, β > 0. (1)

похожему на уравнение радиоактивного распада и совпадающего с ним при а < β (если а и β постоянные) – при их выводе использовались одинаковые соображения.

Интегрирование уравнения дает

N (t) = N (0) exp 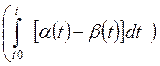, или N (t)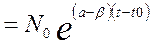

где N (0) = N (t= t₀) – начальная численность.

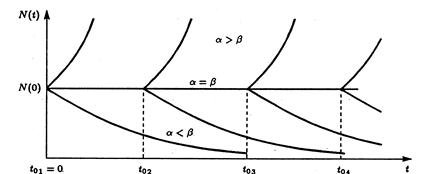
Изменение численности популяции со временем

Из полученного равенства следует, что если a > β, то при t → ∞ число особей х → ∞. С другой стороны, если а < β, то х →0 при t → ∞ и популяция становится вымирающей.

На рисунке приведены графики функции при постоянных а и β (разным подобным кривым соответствуют разные t₀ - значения времени начала процесса). При а = β численность остается постоянной, т.е. в этом случае решением уравнения является равновесная величина N (t) = N (0). Равновесие между рождаемостью и смертностью неустойчиво – даже небольшое нарушение приводит ко все большему отклонению функции N (t) от равновесного значения N (0).

Рассмотрен идеальный случай – сложнейший процесс изменения численности популяции не отвечает реальности – зависит, например, от скорости воспроизводства (определяется частотой встреч особей различного пола), ограниченности доступных ресурсов и др.

Популяционные модели становятся нелинейными, если принять во внимание некоторые дополнительные соображения (скорость воспроизводства определяется частотой встреч особей различного пола, ограниченность доступных ресурсов и др.).

В этом случае в дифференциальном уравнении 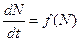функция f (N) – нелинейная.

Дата добавления: 2014-08-04; просмотров: 425; Нарушение авторских прав

Мы поможем в написании ваших работ!