
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Общий вид оптимизационных математических моделей принятия решений в производственных задачах
Для построения и исследования математических моделей, в том числе и моделей принятия решений, направленных на обеспечение оптимальных значений параметров, характеризующих производственный процесс, возникает необходимость их формализации в наиболее общем виде.
Моделирование осуществляется путем описания закономерностей изучаемого объекта с помощью математических выражений (уравнений, неравенств и их систем). Поскольку в качестве критерия оптимальности обычно применяется экономический показатель, модели называются экономико-математическими, а метод решения задач — экономико-математическим моделированием. В зависимости от поставленных задач и метода их решения различают различные типы моделей. Среди них модели линейного и динамического программирования, сетевые, игровые, массового обслуживания, корреляционные, и т.д. Успешность моделирования и эффективность решения любой задачи зависит от двух главных факторов: насколько правильно модель отражает суть объекта (процесса) и насколько правильно выбран критерий оптимальности (оценки эффективности), т. е. насколько модель и критерий, положенный в основу модели, соответствуют поставленной цели.
Очень важным принципом является учет вероятностного характера всей или части информации о технико-экономических и социально-экономических показателях работы предприятия. Математическая модель может быть детерминированной, когда входящие в нее показатели определяются с высокой степенью точности и искомые параметры тоже устанавливаются точно, одним числом. Модель становится вероятностной, когда один или более входящих в нее показателей определяются неточно, с той или иной возможностью отклонения, и искомые величины могут быть установлены лишь с той или иной вероятностью.
Остановимся, коротко, на описании некоторых свойств оптимизационных моделей, которые должны быть отражены при их формализации. Все задачи принятия решения, с которыми приходиться сталкиваться и соответствующие им модели делят на статические и динамические. Статическими задачами принятия решений называют такие задачи, в которых переменные не зависят от времени. В динамических задачах переменные зависят от времени. Также выделяют детерминированные модели, (параметры в таких задачах являются постоянными величинами) и стохастические модели, параметры которых являются случайными величинами. Исходя из определения принятия «правильного решения» математическая модель принятия решений должна содержать одну или несколько целевых функций, а также ряд ограничений.Поэтому, значительное количество математических моделей принятия оптимальных технических решений, в достаточно общем случае, могут быть формализованы в виде, определяемом выражением 3.1.
Как было показано в главе 1, в самом общем случае параметры задачи (которые не являются оптимизируемыми) представляют собой четыре подмножества величин. 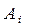
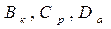 .
.
Первое выражение (3.1) формализует 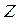 целевых функций модели относительно массива неизвестных.
целевых функций модели относительно массива неизвестных. 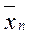 . Второе и третье выражения (3.1) формализуют, соответственно
. Второе и третье выражения (3.1) формализуют, соответственно 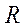 ограничений и
ограничений и 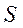 условий, которым должны удовлетворять переменные параметры модели. Параметр
условий, которым должны удовлетворять переменные параметры модели. Параметр 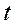 указывает на то, что модель является динамической.
указывает на то, что модель является динамической.
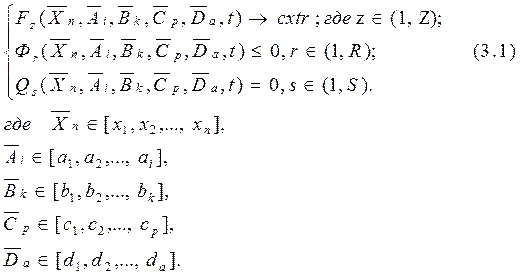
Рассмотрим подмножества параметров, 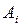
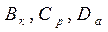 , которые считаются известными, определим их смысл и возможные значения.
, которые считаются известными, определим их смысл и возможные значения.
Если подмножества параметров 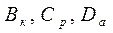 пустые, (т. е. все их элементы равны нулю ), и только значения элементов подмножества
пустые, (т. е. все их элементы равны нулю ), и только значения элементов подмножества 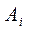 не равны нулю, то говорят о моделировании в условиях полной определенности и модель является детерминированной.
не равны нулю, то говорят о моделировании в условиях полной определенности и модель является детерминированной.
Если же подмножества 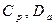 пустые , а заданы лишь значения элементов
пустые , а заданы лишь значения элементов 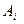 и
и 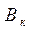 , то говорят о моделировании в условиях статистической определенности. В этом случае подмножество известных параметров задачи
, то говорят о моделировании в условиях статистической определенности. В этом случае подмножество известных параметров задачи 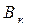 являются случайными величинами с известным законом распределения.
являются случайными величинами с известным законом распределения.
Суть моделирования в условиях статистической определенности состоит в том, что исходные данные задачи содержат случайные величины с известным законом распределения, и как следствие, неизвестные величины могут носить случайный характер, закон распределения и другие характеристики которых следует определить в процессе решения задачи.
В том случае, если в качестве исходных данных модель содержит не пустое подмножество случайные величин 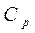 ,закон распределения которых не известен, то говорят о моделировании в условиях не определенности.
,закон распределения которых не известен, то говорят о моделировании в условиях не определенности.
Так же следует различать моделирование в условиях противодействия. Моделирование в условиях противодействия заключается в том, что достижению формализованной в модели цели активно противодействует разумный противник. Это противодействие описывается некоторым подмножество параметров  , которые считаются известными и представляют собой постоянные неслучайные величины.
, которые считаются известными и представляют собой постоянные неслучайные величины.
Математическая модель некоторого производственного процесса, формализованная в виде выражения (3.1) и содержащая в качестве известных параметров подмножеств величин 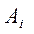 ,
, 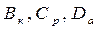 , в самом общем случае представляет собой сложную оптимизационную математическую задачу. Для получения результата ее численного решения необходимо разработать и реализовать некоторый специальный алгоритм, в основу которого, как правило, положен некоторый математический метод, определяемый используемым в модели методом оптимизации. Формализованная в виде (3.1) модель имеет, достаточно, общий вид.
, в самом общем случае представляет собой сложную оптимизационную математическую задачу. Для получения результата ее численного решения необходимо разработать и реализовать некоторый специальный алгоритм, в основу которого, как правило, положен некоторый математический метод, определяемый используемым в модели методом оптимизации. Формализованная в виде (3.1) модель имеет, достаточно, общий вид.
Ряд моделей используемых н практике могут быть формализованы в более простом виде. Это касается и такого случая, когда задача (3.1) не формализуется как оптимизационная. Если в первом выражении (3.1) заменить « 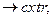 » на «
» на « 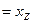 », то получим один из частных случаев формализации математических моделей. Этот частный случай описывает и аналитическую взаимозависимость между независимыми и зависимыми переменными, взаимозависимость в виде дифференциальных уравнений первого и второго порядков, а также взаимозависимость в виде систем дифференциальных уравнений ( линейных и более высоких порядков).
», то получим один из частных случаев формализации математических моделей. Этот частный случай описывает и аналитическую взаимозависимость между независимыми и зависимыми переменными, взаимозависимость в виде дифференциальных уравнений первого и второго порядков, а также взаимозависимость в виде систем дифференциальных уравнений ( линейных и более высоких порядков).
§3.4 Формализация имитационных математических моделей. Основные понятия о методе имитационного моделирования.
Имитационное моделирование, приобретает все большее значение с развитием современных вычислительных средств, в том числе персональных компьютеров и их сетей. С высокой долей достоверности можно утверждать, что имитационное моделирование не теория, а методика решения проблем.
Как указывалось в ряде работ, посвященных имитационному моделированию, последнее представляется не как теория, а как методология.
Метод имитационного моделирования может быть сравним с такими методами теории исследования операций, как вероятностные методы, методы статистических оценок, методы целочисленного линейного и нелинейного программирования, методы теории массового обслуживания, методы сетевых моделей, методы теории игр.
В начале своего развития, когда средства вычислительной техники не были доступными и эффективными, метод имитационного моделирования рассматривался некоторыми исследователями приближенным грубым приемом и последним средством, к которому следует прибегнуть для решения задачи. Однако неоспоримым является тот факт, что на современном уровне развития средств вычислительной техники метод имитационного моделирования является одним из распространенных и востребованных методов.
Все имитационные модели можно представить себе в виде модели, так называемого «черного ящика». Они обеспечивают выдачу выходного сигнала системы, если на ее входные подсистемы поступит некоторый входной сигнал. Поэтому для получения искомых результатов решения практических задач следует осуществить имитационный эксперимент на имитационных моделях, а не «решать» вышеназванные задачи. Имитационные модели не способны формировать свое собственное решение в том виде, в каком это имеет место в математических (аналитических) моделях.
Такое представление имитационного моделирования объясняет определенную условность его применения для решения ряда практических научных задач, т. е. делает его применение, в некотором смысле, искусством в силу отсутствия общих правил и подходов для такого применения. Суть не в методе имитационного моделирования, а в искусстве его применения.
Следует отметить, что метод имитационного моделирования, наряду с преимуществами, имеет и ряд существенных недостатков. К ним можно отнести отсутствие универсальных алгоритмов и правил построения имитационных экспериментов, а также строгих правил формализации самих имитационных моделей. Построение имитационной математической модели некоторой практически важной проблемы подразумевает выполнение таких же этапов, что и при формализации аналитических математических задач. Отсутствие некоторых общих правил предполагает использование творческого подхода для построения имитационных моделей. В этом случае большое значение приобретает не сам метод, а навыки эффективного им пользования.
Все вышеназванные трудности являются тем ограничением, которое не позволяет в достаточной мере применять методы имитационного моделирования для решения многих практических задач. Поэтому необходимо установить и алгоритмизировать процесс построения имитационных математических моделей.
Ниже обосновывается подход для построения таких имитационных математических моделей, а также сделана попытка упорядочить этот процесс. Тем самым искусство построения имитационных моделей частично алгоритмизируется, что делает этот процесс более предсказуемым.
Определим имитационную модель физических и организационно-технологических процессов, как некоторую установленную взаимосвязь между существенными параметрами, определяющими процесс (объект) исследования. Причем установленные зависимости таковы, что позволяют количественно оценить изменение каждого из параметров модели в зависимости от значений одного или нескольких других параметров модели. Из данного определения следует, что создание модели включает в себя формулировку (согласно требованиям решения некоторой практической проблемы) формализацию модели и ее преобразование к виду, удобному для проведения имитационного эксперимента. В монографии [1] предлагается способ построения (формализации) имитационных математических моделей, которые могут быть использована успешны, в том числе, и для численного решения задач оптимизации.
Численно решить сложную практическую задачу, формализованную системой уравнения (3.1) не всегда представляется возможным. Построение алгоритма поиска оптимальных значений неизвестных параметров задачи само по себе является сложной математической задачей, особенно при том, что постоянные (известные) параметры этой задачи содержат различные типы случайных величин.
Для таких случаев используется такой подход, который является относительно новым в математике и называется методом имитационного моделирования. Имитационное моделирование состоит в многократном воспроизведении функционирования (поведения) исследуемой системы на основе математической модели. Результаты одного имитационного эксперимента представляют собой значение одной части множества параметров характеризующих исследуемый процесс, явление (называемых зависимыми) в зависимости от заданных значений другой части параметров, называемых независимыми. Другими словами, результаты имитационного эксперимента представляют собой совокупность наборов некоторых показателей, являющихся критериями оценки поведения моделируемого процесса, явления, свойств объекта в зависимости от значений некоторого подмножества параметров полно и однозначно описывающих исследуемый процесс, явление, свойства объекта и позволяющих рассчитать значения критериев.
Суть использования метода имитационного моделирования для решения задач, формализованных в виде аналитических выражений (3.1) заключается в следующем. Необходимо в выражение (3.1) подставлять числовые значения независимых параметров и находить соответствующие им значения зависимых параметров. Другими словами, решения формализованной задачи (3.1) может быть найдено путем подбора значений части неизвестных величин и вычислений остальной части неизвестных величин из выражения (3.1) на основе подобранной части неизвестных параметров. Имитационный эксперимент , как правило, полностью проводится на ЭВМ.
При решении задач методом имитационного моделирования, в отличии от решения этих задач аналитическими методами, алгоритм поиска неизвестных величин не строится. В место этого разрабатывается алгоритм проведения численного эксперимента на имитационной модели. Суть подготовки численного эксперимента состоит в том, что бы изначально выбрать некоторое количество наборов (подмножеств) неизвестных независимых параметров. Затем, по значениям этих переменных, из целевой (целевых) функции имитационной модели определяется подмножество критериев (зависимых переменных). Далее, сформированный таким образом вариант, состоящий из этих двух подмножеств переменных, проверяются на удовлетворяемость условиям и ограничениям модели. Если этот вариант удовлетворяет условиям и ограничениям модели, то он является решением задачи, но не обязательно оптимальным. Эксперимент повторяется многократно и формируется множество возможных вариантов решений. Затем по специальному алгоритму, с учетом, как правило, нескольких критериев, выбирается наилучшее из сформированных решений. Следует особенно отметить, что полученное таким образом решение не обязательно будет являться оптимальным. Для того, чтобы это решение было оптимальным, или квазиоптимальным необходимо провести численный эксперимент со всеми возможными решениями. В этом случае есть уверенность, что наилучшее решение содержится среди вариантов подготовленных для проведения численного эксперимента. Формирование множества всех возможных вариантов решений является отдельной, как правило, не простой задачей. Она усложняется еще тем, что большая размерность этого множества, требует применения более мощных вычислительных средств.
Таким образом, имитационной математической моделью является модель, у которой одна часть, неизвестных параметров, описывающих исследуемые свойства объекта, выражается в виде некоторой количественной и логической зависимости от остальных параметров, описывающих свойства объекта. При этом, вторая часть неизвестных является независимыми величинами, т.е. они могут принимать произвольные значения из области допустимых значений. Задавая по определенным законам значения одним параметрам, можно получить значение остальных параметров. Далее, полученные решения проверяются на удовлетворяемость условиям и ограничениям и из них выбирается наилучшее по заданным критериям.
§3.5 Формализация интуитивных эвристических моделей и алгоритмы их построения.
Наиболее распространенным и часто используемым на практике способом моделирования является моделирование исследуемых (оптимизируемых) процессов и явлений в нашем воображении. Выбор оптимальных параметров характеризующих исследуемый процесс осуществляется, при этом, на основе интуиции, эвристического способа принятия решений с использованием всей доступной информации об исследуемом процессе, явлении, объекте. Такой вид моделирования, иногда, еще называют мысленным моделированием. Повышенный интерес у специалистов, занимающихся решением конкретных производственных задач, вызывают интуитивные эвристические модели, особенно, в связи с развитием информационных технологий. Одной из форм представления интуитивных эвристических моделей (ИЭМ) являются диалоговые компьютерные программы. Естественным выглядит вопрос о максимальной автоматизации процесса мысленного моделирования. Под автоматизацией интуитивного эвристического моделирования понимаем предоставление максимальной информации, ее предварительная обработка, возможность качественной и количественной оценки принимаемых решений для проведения мысленного эксперимента. Поэтому, для достижения максимального практического эффекта современные компьютерные модели, кроме ИЭМ должны включать – информационные, оптимизационные математические, имитационные модели. Для разработки таких моделей необходимы более совершенные способы формализации ИЭМ.
Интуитивными эвристическими моделями производственных процессов назовем способы (алгоритмы) реализованные на ЭВМ, определения исследователем неизвестных параметров, описывающих моделируемый процесс с использованием своей интуиции, знаний, опыта на основе представленной ему информации в определенном объеме, форме и временном интервале.
На основании выполненных исследований делается вывод о том, что алгоритм построения интуитивных моделей на базе современных информационных технологий должен включать следующие основные этапы:
1. Определение перечня (множества) неизвестных параметров, которые предполагается определить в результате интуитивного моделирования.
2. Определение вида, объемов, формы и, в случае необходимости, времени представления информации.
3. Определение источников информации, в том числе информационные математические модели, массивы баз данных локальных и других компьютерных сетей.
4. Разработку алгоритмов (способов) определения исследователем неизвестных величин с использованием своей интуиции и предоставленной ему информации;
5. Преобразование информации и ввод в компьютер значений определяемых переменных.
Следует отметить ту важную роль, которую играют в процессе поиска решений информационные математические модели, позволяющие получить необходимую исходную информацию в результате математической обработки определенных информационных потоков.
Вышеизложенное более подробно описано в монографии 1.
| <== предыдущая страница | | | следующая страница ==> |
| Основные закономерности формализации моделей | | | Аналитико-экспериментальный метод формализации математических моделей принятия оптимальных решений |
Дата добавления: 2014-08-04; просмотров: 744; Нарушение авторских прав

Мы поможем в написании ваших работ!