
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Адаптация эконометрических моделей
Пример
Динамические модели авторегрессии
Модель называется динамической моделью авторегрессии, если результатный признак зависит не только от времени и значений факторных признаков, но и от значений результатного признака в предыдущие моменты (промежутки) времени.
Например: 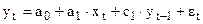 .
.
Здесь а1 характеризует краткосрочное изменение yt под действием изменения xt на 1 ед. К моменту t + 1 результат yt изменится под действием изменения изучаемого фактора в момент времени t на a1 ед., а yt+1 под воздействием своего изменения в непосредственно предшествующий момент времени – на с1 ед. Таким образом, общее абсолютное изменение результата в момент t + 1 составит 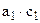 ед. Аналогично в момент времени t + 2 абсолютное изменение результата составит
ед. Аналогично в момент времени t + 2 абсолютное изменение результата составит 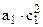 ед. и т. д. Следовательно, долгосрочный мультипликатор в модели авторегрессии можно рассчитать как сумму краткосрочного и промежуточного мультипликаторов:
ед. и т. д. Следовательно, долгосрочный мультипликатор в модели авторегрессии можно рассчитать как сумму краткосрочного и промежуточного мультипликаторов:
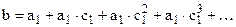
В модели авторегрессии вводится условие стабильности, то есть 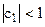 . Поэтому:
. Поэтому:
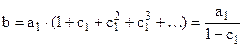 .
.
По данным о динамике потребления и дохода в регионе получена модель авторегрессии:
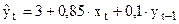 .
.
Таким образом, краткосрочный мультипликатор равен 0,85– это предельная склонность к потреблению в краткосрочном периоде. Следовательно, увеличение среднедушевого совокупного дохода на 1 тысячу рублей приводит к росту объема потребления в тот же год в среднем на 850 рублей. Долгосрочную склонность к потреблению можно определить в соответствии с формулой: 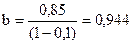 , то есть в долгосрочной перспективе рост среднедушевого совокупного дохода на 1 тысячу рублей приведёт к росту объема потребления в среднем на 944 рубля.
, то есть в долгосрочной перспективе рост среднедушевого совокупного дохода на 1 тысячу рублей приведёт к росту объема потребления в среднем на 944 рубля.
4.8. Выравнивание одномерного временного ряда
Как показано выше, в основе моделирования динамических зависимостей лежит моделирование одномерных динамических рядов, структура которых характеризуется наличием трендов, циклических и случайных колебаний. Поэтому рассмотрим, каким образом происходит выделение трендов и циклических колебаний. Это означает в первую очередь устранение случайной составляющей и в зависимости от цели исследования либо выделение трендовой, либо циклической составляющей.
Основными методами выделения трендов являются: фильтрация, с помощью которой происходит как случайной, так и циклической составляющей, и аналитическое описание, т.е. аппроксимация какой-либо подходящей аналитической зависимости. Для аналитического описания используется МНК. Основными методами выделения циклических составляющих (волн) также являются: фильтрация (для устранения случайных колебаний), устранение глобального тренда и аналитическое описание с помощью МНК путем расположения в ряды Фурье. Фильтрация чаще всего производится путем использования метода скользящих средних. Путем изменения диапазона чисел, для которых определяется средняя величина, изменяется порог фильтрации.
Рассмотрим процесс построения динамической модели на основе рассмотренного выше примера. Предварительный визуальный и автокорреляционный анализ показал наличие в уровнях динамического ряда значительной циклической и трендовой составляющих.
Выравнивание исходного ряда методами скользящей средней:
| t | 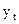
| 
| Скол. сред. (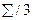 ) )
|
| 0,5 | |||
| 2,7 | 9,7 | 3,23 | |
| 6,5 | 13,9 | 4,63 | |
| 4,7 | 13,5 | 4,5 | |
| 2,3 | 12,2 | 4,07 | |
| 5,2 | 5,33 | ||
| 8,5 | 20,8 | 6,93 | |
| 7,1 | 21,6 | 7,2 | |
| 20,1 | 6,7 | ||
| 24,2 | 8,07 | ||
| 11,2 | 28,2 | 9,4 | |
| 29,4 | 9,8 | ||
| 8,2 | 27,4 | 9,13 | |
| 9,2 | 29,9 | 9,97 | |
| 12,5 | 34,9 | 11,63 | |
| 13,2 | 36,2 | ||
| 10,5 |
При выравнивании по 5 членам получим:
| t | 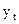
| 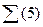
| Скол. сред. 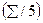
| Скол. сред. 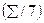
|
| 0,5 | ||||
| 2,7 | ||||
| 6,5 | 16,7 | 3,34 | ||
| 4,7 | 21,4 | 4,28 | 4,34 | |
| 2,3 | 27,2 | 5,44 | 5,29 | |
| 5,2 | 27,8 | 5,56 | 5,76 | |
| 8,5 | 29,1 | 5,82 | 5,83 | |
| 7,1 | 33,8 | 6,76 | 6,76 | |
| 39,8 | 7,96 | 7,86 | ||
| 41,3 | 8,26 | 8,89 | ||
| 11,2 | 42,4 | 8,48 | 8,39 | |
| 45,6 | 9,12 | 9,16 | ||
| 8,2 | 51,1 | 10,22 | 9,19 | |
| 9,2 | 53,1 | 10,62 | 10,69 | |
| 12,5 | 53,6 | 10,72 | ||
| 13,2 | ||||
| 10,5 |
При средней по трем членам имело место проявления цикличности, а при средней по 5 членам цикличность проявляется не так заметно. Сглаживание по 7 членам не дает значительного снижения цикличности. Построим график скользящей средней по 5 членам:
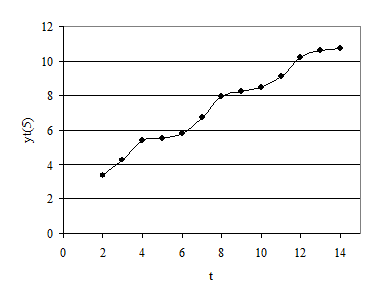 |
С помощью МНК (с помощью STATGRAPHICS) определим трендовую составляющую (линейную)
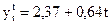 .
.
При этом коэффициент детерминации 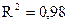 , коэффициент корреляции r = 0,99.
, коэффициент корреляции r = 0,99.
Таблица ряда при этом примет вид:
| t | 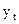
| 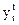
| 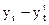
|
| 0,5 | 2,37 | -1,87 | |
| 2,7 | 3,01 | -0,31 | |
| 6,5 | 3,65 | 2,85 | |
| 4,7 | 4,29 | 0,41 | |
| 2,3 | 4,93 | -2,63 | |
| 5,2 | 5,57 | -0,37 | |
| 8,5 | 6,21 | 2,29 | |
| 7,1 | 6,85 | 0,25 | |
| 7,49 | -1,4 | ||
| 8,13 | -1,13 | ||
| 11,2 | 8,77 | 2,43 | |
| 9,41 | 0,59 | ||
| 8,2 | 10,05 | -1,85 | |
| 9,2 | 10,69 | -1,49 | |
| 12,5 | 11,33 | 1,17 | |
| 13,2 | 11,97 | 1,23 | |
| 10,5 | 12,61 | -2,11 |
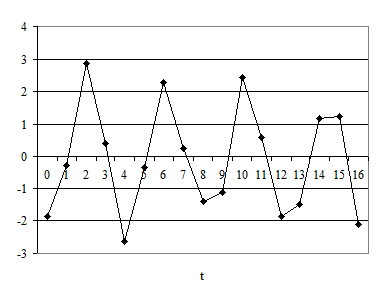 |
Далее выделим сумму циклической и случайной составляющей
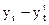 и нанесем её на график:
и нанесем её на график:
Выделение циклической составляющей производится путем разложения в ряд Фурье

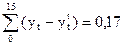
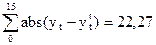
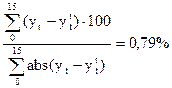 , т.е.
, т.е. 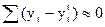
(суммы берутся от 0 до 15, так как 16 – начало нового цикла).
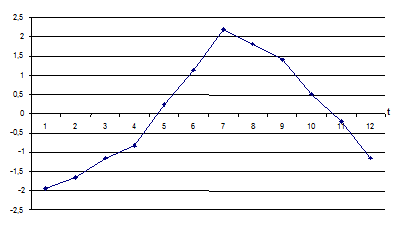
Увеличим число точек до 12 на одном цикле (цикл = 4) и найдем средние показатели циклической волны.
| t | 
| 
| 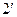
| 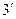
| 
| 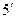
|
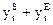 0 - 4
0 - 4
| -1,87 | -1 | -0,5 | -0,31 | 0,8 | 1,8 |
| 4 - 8 | -2,63 | -1,8 | -1 | -0,37 | 0,5 | 1,3 |
| 8 – 12 | -1,4 | -1,8 | -1,5 | -1,13 | 0,2 | |
| 12 - 16 | -1,85 | -2 | -1,6 | -1,49 | -0,5 | 0,5 |
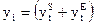
| -1,94 | -1,65 | -1,15 | -0,825 | 0,25 | 1,15 |
| t | 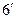
| 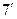
| 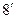
| 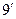
| 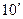
| 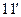
|
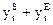 0 - 4
0 - 4
| 2,85 | 1,3 | 0,41 | -0,4 | -1,5 | |
| 4 - 8 | 2,29 | 1,9 | 1,2 | 0,25 | -0,3 | -0,8 |
| 8 – 12 | 2,43 | 1,9 | 1,2 | 0,59 | -0,2 | -0,8 |
| 12 - 16 | 1,17 | 1,8 | 1,23 | 0,1 | -1,5 | |
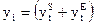
| 2,185 | 1,8 | 1,4 | 0,52 | -0,2 | -1,15 |
 Используем разложение в ряд Фурье:
Используем разложение в ряд Фурье:
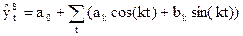
k – номер гармоники ряда Фурье.
Для отыскания параметров уравнения используется МНК:
 , найдя частные производные и приравняв нулю, получим формулы для вычисления параметров:
, найдя частные производные и приравняв нулю, получим формулы для вычисления параметров:
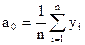
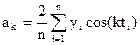
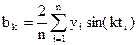
В нашем случае:
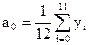
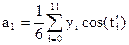
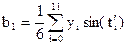
Каждому отсчету ti соответствует своя фаза.
| |||||||
| Фаза | 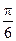
| 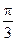
| 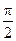
| 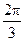
| 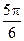
| 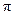
| |
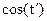
| 0,866 | 0,5 | -0,5 | -0,866 | -1 | ||
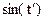
| 0,5 | 0,866 | 0,866 | 0,5 | |||
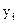
| -1,97 | -1,65 | -1,15 | -0,825 | 0,25 | 1,15 | 2,185 |
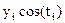
| -1,94 | -1,43 | -0,57 | -0,125 | -1 | -2.2 | |
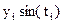
| -0,82 | -1 | -0,82 | 0,22 | 0,57 | ||

| -1,726 | -1,81 | -1,39 | -0,6 | 0,37 | 1,25 | 1,8 |
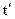
| ||||||
| Фаза | 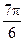
| 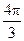
| 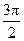
| 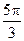
| 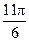
| |
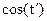
| -0,866 | -0,5 | 0,5 | 0,866 | ||
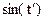
| -0,5 | -0,866 | -1 | -0,866 | -0,5 | |
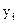
| 1,8 | 1,4 | 0,62 | -0,2 | -1,15 | |
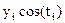
| -1,56 | -0,69 | -0,1 | -1 | -1,94 | |
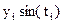
| -0,9 | -1,2 | -0,62 | -0,17 | 0,57 | |

| 1,88 | 1,47 | 0,67 | 0,29 | -1,17 | -1,726 |
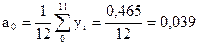 (почти 0)
(почти 0)
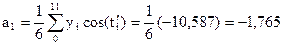
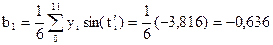
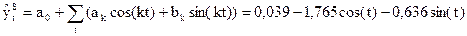
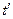
| 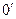
| 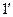
| 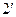
| 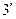
| 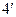
| 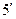
| 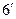
|

| -1,726 | -1,81 | -1,39 | -0,6 | 0,37 | 1,25 | 1,8 |
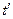
| 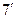
| 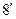
| 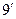
| 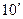
| 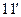
| 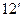
|

| 1,88 | 1,47 | 0,67 | 0,29 | -1,17 | -1,726 |
Приближение будет более точным при учете 2-ой гармоники.
В целом  имеют вид:
имеют вид:
| t | 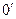
| 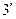
| 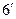
| 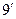
| 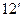
| 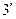
| 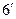
| 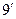
| 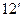
|
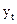
| 0,5 | 2,7 | 6,5 | 4,7 | 2,3 | 5,2 | 8,5 | 7,1 | |
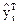
| 2,37 | 3,01 | 3,65 | 4,29 | 4,93 | 5,57 | 6,21 | 6,85 | 7,49 |
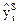
| -1,73 | -0,6 | 1,8 | 0,67 | -1,73 | -0,6 | 1,8 | 0,67 | -1,73 |
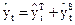
| 0,64 | 2,41 | 5,45 | 4,96 | 3,2 | 4,97 | 8,01 | 7,52 | 5,76 |
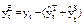
| -0,14 | 0,29 | 1,05 | -0,26 | -0,9 | 0,23 | 0,49 | -0,42 | 0,24 |
| t | 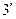
| 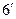
| 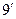
| 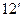
| 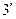
| 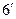
| 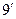
|
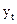
| 11,2 | 8,2 | 9,2 | 12,5 | 13,2 | ||
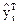
| 8,13 | 8,77 | 9,41 | 10,05 | 10,69 | 11,33 | 11,97 |
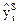
| -0,6 | 1,8 | 0,67 | -1,73 | -0,6 | 1,8 | 0,67 |
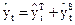
| 7,53 | 10,57 | 10,08 | 8,32 | 10,09 | 13,13 | 12,84 |
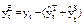
| -0,53 | 0,63 | -0,08 | -0,12 | -0,89 | -0,63 | 0,36 |

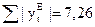
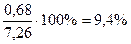 т.е. в пределах 10%
т.е. в пределах 10%
Таким образом, общая модель динамического процесса имеет вид:
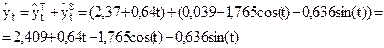
Определим ошибки аппроксимации:
| t | ||||||||

| 0,5 | 2,7 | 6,5 | 4,7 | 2,3 | 5,2 | 8,5 | 7,1 |
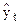
| 0,64 | 2,41 | 5,45 | 4,96 | 3,2 | 4,97 | 8,01 | 7,52 |
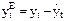
| -0,14 | 0,29 | 1,05 | -0,26 | -0,9 | 0,23 | 0,49 | -0,42 |
| t | ||||||||

| 11,2 | 8,2 | 9,2 | 12,5 | 13,2 | |||
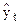
| 5,76 | 7,53 | 10,57 | 10,08 | 8,32 | 10,09 | 13,13 | 12,84 |
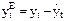
| 0,24 | -0,53 | 0,63 | -0,08 | -0,12 | -0,89 | -0,63 | 0,36 |
Средняя линейная ошибка аппроксимации:
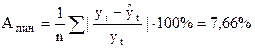
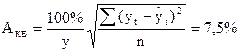
Практически одинаково.
Таким образом, можно сделать ближайший прогноз значения функции.
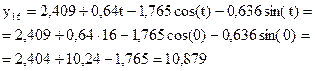
(истинное значение 10,5)
Адаптация эконометрической модели – это процесс её корректировки на основе вновь поступающей информации, то есть, процесс приспособления ее, к изменившимся условиям формирования моделируемого явления. Адаптация направлена на повышение адекватности модели путём использования текущих новых значений признаков, не известных при её построении.
Можно выделить пространственную и временную адаптацию.
При пространственной адаптации после построения модели множественной регрессии продолжается процесс наблюдения и получения новых данных, на основе корректируются параметры модели.
При временной адаптации используется сдвиг данных, то есть при получении новых данных исключается из рассмотрения часть первоначальных данных, в результате чего модель адаптируется к изменившимся условиям формирования исследуемого явления.
Дополнительным методом временной адаптации является присвоение новым данным больших весов при этом сумма весов, как правило, равна 1.
Рассмотрим адаптацию с использованием разных весов, присваиваемых различным данным. В принципе, веса можно присваивать исходя из предпочтений исследователя, однако разработан ряд специальных методов. Рассмотрим наиболее простой из них – метод гармонических весов.
При использовании этого метода производится сглаживание с помощью метода скользящих трендов, более поздним данным присваиваются большие веса, которые рассчитываются определённым образом, вычисляется средний взвешенный прирост, который используется для прогнозирования следующего уровня динамического ряда. Алгоритм метода может быть представлен следующим образом.
1. Производится сглаживание методом скользящих трендов.
Выбирается число последовательных точек наблюдения для построения скользящих трендов  . Обычно
. Обычно 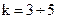

Тренды описываются выражением 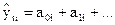 ,
, 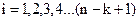 , где
, где  - общее число точек наблюдения. Параметры трендов определяются с помощью МНК.
- общее число точек наблюдения. Параметры трендов определяются с помощью МНК.
2. Определяются средние расчетные значения уровней ряда на основе уравнений трендов.
3. По полученным расчётным значениям уровней ряда рассчитываются абсолютные приросты.
4. Рассчитываются гармонические веса по формуле
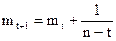 ,
, 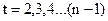
5. Определяются гармонические коэффициенты по формуле
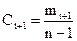 ,
, 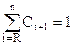
6. Определяется средневзвешенное значение прироста.
7. Последующий уровень временного ряда определяется путём прибавления к последующему расчётному значению ряда динамики среднего прироста.
Этот метод может быть использован при выполнении основных предпосылок:
1. Исследуемое экономическое явление должно наблюдаться достаточно продолжительное время, быть инерционным, временной ряд не должен иметь значительных скачкообразных изменений.
2. Отклонения от скользящего тренда должны представлять собой случайный процесс.
 Рассмотрим один из возможных способов временной адаптации с использованием сдвига данных.
Рассмотрим один из возможных способов временной адаптации с использованием сдвига данных.
Пусть статистическая зависимость имеет вид:
| t | ||||||||||
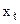
| 5.31 | 5.42 | 6.07 | 6.11 | 6.53 | 6.04 | 7.38 | 7.46 | 7.58 | 7.8 |
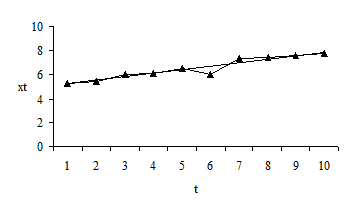
Тренд имеет вид: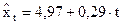 ;
; 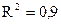 .
.
Пусть в следующем году 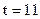 ,
, 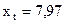 ; тогда тренд с учетом новой информации без значения
; тогда тренд с учетом новой информации без значения 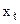 при
при  :
:
 ,
, 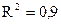 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Решение. Даны 2 параллельных временных ряда | | | Прогнозная статистическая экстраполяция |
Дата добавления: 2014-03-19; просмотров: 648; Нарушение авторских прав

Мы поможем в написании ваших работ!