
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Решение. Даны 2 параллельных временных ряда
Пример 3
Даны 2 параллельных временных ряда. Необходимо определить, имеется ли между этими показателями корреляционная зависимость.
| t | |||||||
| xt | 2,2 | 2,8 | 3,2 | 3,6 | 4,1 | 4,8 | 5,3 |
| yt | 4,8 | 5,6 | 6,2 | 6,6 | 7,3 | 8,1 | 8,8 |
1. а) Построим график:
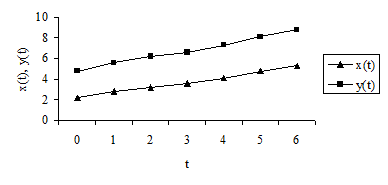 |
Т. е. имеет место практически линейная зависимость от времени для каждого из показателей xt и yt.
б) Определим непосредственную корреляцию между этими показателями: rxy = 0,9989  .
.
На самом деле это, возможно, говорит лишь об одинаковых и достаточно выраженных тенденциях, то есть почти о корреляции между t и t, но не о корреляции между x и y. О том же говорят и коэффициенты корреляции:
| xt | 2,2 | 2,8 | 3,2 | 3,6 | 4,1 | 4,8 |
| xt+1 | 2,8 | 3,2 | 3,6 | 4,1 | 4,8 | 5,3 |
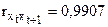
| yt | 4,8 | 5,6 | 6,2 | 6,6 | 7,3 | 8,1 |
| yt+1 | 5,6 | 6,2 | 6,6 | 7,3 | 8,1 | 8,8 |
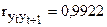
Непосредственная зависимость: 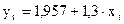
в) Для того, чтобы определить корреляцию между x и y, необходимо устранить тенденции. Для этого определим тренды:
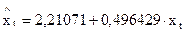 ,
,
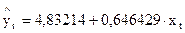
Теперь вычислим разности: 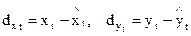
| t | |||||||
| xt | 2,2 | 2,8 | 3,2 | 3,6 | 4,1 | 4,8 | 5,3 |
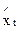
| 2,21 | 2,707 | 3,20 | 3,7 | 4,20 | 4,69 | 5,190 |
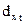
| -0,01 | 0,09 | -0,03 | -0,10 | -0,096 | 0,11 | 0,011 |
| yt | 4,8 | 5,6 | 6,2 | 6,6 | 7,3 | 8,1 | 8,8 |
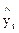
| 4,83 | 5,48 | 6,12 | 6,77 | 7,42 | 8,06 | 8,71 |
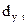
| -0,03 | 0,12 | 0,075 | -0,171 | -0,118 | 0,03 | 0,09 |
Определим зависимости 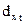 и
и 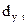 :
: 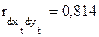
При этом автокорреляция остатков:
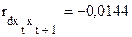
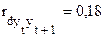 ,
,
т. е. при данном числе данных автокорреляция практически незначима.
Таким образом, между x и y имеется определенная и достаточно сильная зависимость:
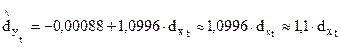 .
.
Однако в данном случае очень невелики диапазоны изменения.
2. Можно было для устранения тренда использовать также метод последовательных разностей.
Применим этот метод в данном случае:
| t | |||||||
| xt | 2,2 | 2,8 | 3,2 | 3,6 | 4,1 | 4,8 | 5,3 |
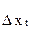
| - | 0,6 | 0,4 | 0,4 | 0,5 | 0,7 | 0,5 |
| yt | 4,8 | 5,6 | 6,2 | 6,6 | 7,3 | 8,1 | 8,8 |
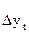
| - | 0,8 | 0,6 | 0,4 | 0,7 | 0,8 | 0,7 |
Определим коэффициенты автокорреляции для разностей:
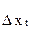
| 0,6 (4) | 0,4 (1,5) | 0,4 (1,5) | 0,5 (3) | 0,7 (5) | 0,5 |

| 0,4 (1,5) (6,25) | 0,4 (1,5) (0) | 0,5 (3,5) (4) | 0,7 (5) (4) | 0,5 (3,5) (2,25) | |
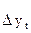
| 0,8 (4,5) | 0,6 (2) | 0,4 (1) | 0,7 (3) | 0,8 (4,5) | 0,7 |
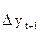
| 0,6 (2) (2,25) | 0,4 (1) (1) | 0,7 (3,5) (6,25) | 0,8 (5) (4) | 0,7 (3,5) (1) |
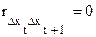
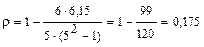

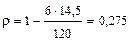
Таким образом, автокорреляция между разностями отсутствует.
Определим зависимость между 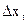 и
и 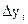 .
.
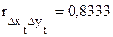 - достаточно высокий коэффициент корреляции (как и в предыдущем случае).
- достаточно высокий коэффициент корреляции (как и в предыдущем случае).
Регрессионная зависимость: 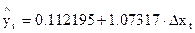
Т. е. при изменении прироста 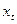 на 1 единицу прирост y изменяется на 1,073 единицы (т. е. почти тот же прирост). Здесь также малы изменения переменных.
на 1 единицу прирост y изменяется на 1,073 единицы (т. е. почти тот же прирост). Здесь также малы изменения переменных.
д) Кроме рассмотренных способов, существует еще один метод исключения тенденции, а именно, метод оснований на включении в модель регрессии по временным рядам фактора времени.
В данном случае строится модель вида:
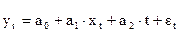 , где параметры
, где параметры 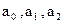 ищутся методом наименьших квадратов.
ищутся методом наименьших квадратов.
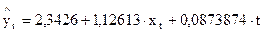
При этом 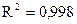 , то есть описание очень хорошее. Это говорит о достаточно высокой зависимости yt от xt. Изменения xt на 1 единицу приведут к увеличению yt на 1,126 единицы – то же самое, что и в предыдущих случаях, но здесь еще дана и поправка на время, т. е. yt зависит как xt1, так и от t. Данный метод в отличие от рассмотренных ранее, позволяет учесть всю информацию, содержащуюся в исходных данных, кроме того, здесь значительные изменения x и y. Представленные примеры показывают специфичность анализа взаимосвязи показателей, поставляющих временные ряды.
, то есть описание очень хорошее. Это говорит о достаточно высокой зависимости yt от xt. Изменения xt на 1 единицу приведут к увеличению yt на 1,126 единицы – то же самое, что и в предыдущих случаях, но здесь еще дана и поправка на время, т. е. yt зависит как xt1, так и от t. Данный метод в отличие от рассмотренных ранее, позволяет учесть всю информацию, содержащуюся в исходных данных, кроме того, здесь значительные изменения x и y. Представленные примеры показывают специфичность анализа взаимосвязи показателей, поставляющих временные ряды.
Проверим модель на адекватность:
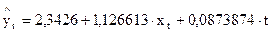
| t | |||||||
| xt | 2,2 | 2,8 | 3,2 | 3,6 | 4,1 | 4,8 | 5,3 |
| yt | 4,8 | 5,6 | 6,2 | 6,6 | 7,3 | 8,1 | 8,8 |
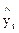
| 4,82 | 5,58 | 6,12 | 6,66 | 7,31 | 8,187 | 8,725 |

| -0,021 | 0,0155 | 0,077 | -0,06 | -0,011 | -0,0873 | 0,0747 |
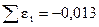 (незначима).
(незначима).
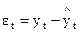
Приложение: необходимость логического анализа.
Если логический анализ показывает, что функция 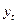 существенно зависит от
существенно зависит от 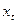 , причем при
, причем при 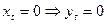 , то можно построить зависимость
, то можно построить зависимость 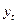 от
от 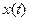 в виде:
в виде:
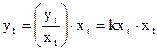 (при этом не должно быть лага).
(при этом не должно быть лага).
И тогда нужно знать лишь зависимость 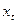 от t и
от t и 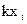 от t.
от t.
В рассматриваемом случае имеем:
| t | |||||||
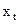
| 2,2 | 2,8 | 3,2 | 3,6 | 4,1 | 4,8 | 5,3 |
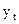
| 4,8 | 5,6 | 6,2 | 6,6 | 7,3 | 8,1 | 8,8 |
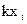
| 2,182 | 1,9375 | 1,833 | 1,78 | 1,6875 | 1,692 |
При этом: 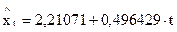
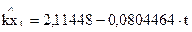
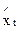
| 2,211 | 2,707 | 3,203 | 3,6999 | 4,196 | 4,693 | 5,189 |
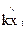
| 2,1145 | 2,034 | 1,953 | 1,873 | 1,793 | 1,712 | 1,6318 |
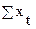
| -0,0107 | 0,9286 | -0,00357 | -0,1 | -0,096 | 0,107 | 0,0107 |
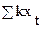
| 0,0675 | -0,034 | -0,0161 | -0,04 | -0,0127 | -0,02475 | 0,0602 |
Сумма по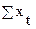 = 0,000021
= 0,000021
Сумма по 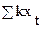 = 0,0000144
= 0,0000144
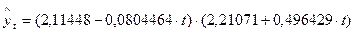
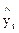
| 4,674 | 5,506 | 6,258 | 6,931 | 7,523 | 8,035 | 8,468 | |
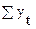
| 0,125 | 0,093 | -0,058 | -0,33 | -0,223 | 0,065 | 0,35 | 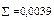
|
Т. е. достаточно хорошее приближение.
При этом коэффициент 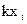 хорошо интерпретируется. Например, если
хорошо интерпретируется. Например, если 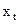 - объем продаж в натуральном выражении, а
- объем продаж в натуральном выражении, а 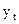 - доходы от продажи данного товара, то
- доходы от продажи данного товара, то 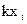 - средняя цена продаж, зависящая в свою очередь от множества факторов.
- средняя цена продаж, зависящая в свою очередь от множества факторов.
| <== предыдущая страница | | | следующая страница ==> |
| Иллюстрирующий проблему лагов и изменения условий | | | Адаптация эконометрических моделей |
Дата добавления: 2014-03-19; просмотров: 335; Нарушение авторских прав

Мы поможем в написании ваших работ!