Геометрическое решение ЗЛП

Тема 11.

Тема 10.

Тема 9.

Тема 8.

Тема 7.

Тема 6.

Тема 5.

Тема 4.

Тема 3.

Тема 2.

Тема 1.

Ответы к тестовым заданиям по темам

1. б. 2. а. 3. в. 4. а. 5. а.

1. б. 2. в. 3. а-4, б-1, в-2. 4. а. 5. б.

1. 1-а, 2-в, 3-б. 2. в. 3. в. 4. 1-б, 2-а, 3-в. 5. в.

1. б. 2. 1-б, 2-в, 3-а. 3. а. 4. г. 5. б.

1. б. 2. а. 3. 1-б, 2-а, 3-в. 4. в. 5. в.

1. в. 2. а. 3. б. 4. в. 5. б.

1. б. 2. а. 3. б. 4. в. 5. г.

1. а, в, г. 2. а. 3. б. 4. а. 5. в.

1. б. 2. в. 3. а. 4. б. 5. в.

1. а. 2. в. 3. в. 4. а. 5. а.

1. в. 2. в. 3. а. 4. а. 5. б.

Если система ограничений задачи линейного программирования представлена в виде системы линейных неравенств с двумя переменными, то такая задача может быть решена геометрически. Метод представляет большой интерес с точки зрения выработки наглядных представлений о сущности задач линейного программирования. Геометрический (или графический) метод предполагает последовательное выполнение ряда шагов. Ниже представлен порядок решения задачи линейного программирования на основе ее геометрической интерпретации.

1. Сформулировать ЗЛП.

2. Построить на плоскости {х₁, х₂} прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.

3. Найти полуплоскости, определяемые каждым из ограничений задачи.

4. Найти область допустимых решений.

5. Построить прямую c₁x₁ + c₂x₂ = h, где h - любое положительное число, желательно такое, чтобы проведенная прямая проходила через многоугольник решений.

6. Перемещать найденную прямую параллельно самой себе в направлении увеличения (при поиске максимума) или уменьшения (при поиске минимума) целевой функции. В результате, либо отыщется точка, в которой целевая функция принимает максимальное (минимальное) значение, либо будет установлена неограниченность функции на множестве решений.

7. Определить координаты точки максимума (минимума) функции и вычислить значение функции в этой точке.

Рассмотрим пример решения ЗЛП графическим методом. Для этого воспользуемся представленной выше задачей о хоккейных клюшках и шахматных наборах.

1. Формулировка задачи приводилась выше, повторим ее: F= 2x₁ + 4x₂ → max;

4x₁ + 6x₂ ≤ 120,

2x₁ + 6x₂ ≤ 72,

x₂ ≤ 10;

x₁ ≥ 0, x₂ ≥ 0

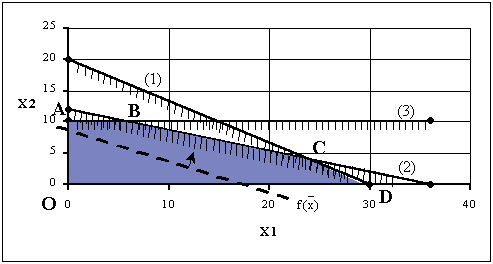
2. Построим прямые, соответствующие каждому из функциональных ограничений задачи (рис. 1). Эти прямые обозначены на рисунке (1), (2) и (3).

Дата добавления: 2014-02-27; просмотров: 638; Нарушение авторских прав

Мы поможем в написании ваших работ!