
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Задачи с решением. 1. В конце каждого года на счет вносится 3000 рублей
1. В конце каждого года на счет вносится 3000 рублей. Определите, какая сумма будет на счете через 3 года, если на вложенные средства начисляются проценты по ставке 14% годовых (сложные).
Необходимо определить будущую стоимость аннуитета (постнумерандо, постоянный, годовой, ограниченный).
По условию задачи: R = 3000 руб., n = 3 года, r = 0,14.
Возможны несколько вариантов записи решения данной задачи:
а) FVpst =
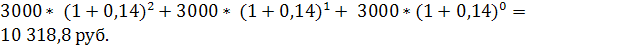 б) б)
б) б) 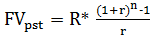 =
= 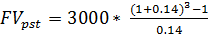 = 10 318.8 руб.
= 10 318.8 руб.
Использование этих двух вариантов возможно, поскольку аннуитет является постоянным. По истечении 3 лет на счете будет находиться 10 318,8 руб.
2. Вы намерены приобрести дачу и для этой цели планируете накопить 10 тысяч руб. в течение 5 лет. Каким должен быть ежеквартальный взнос в банк (постнумерандо), если банк предлагает 12% годовых, начисляемых ежеквартально.
В данной задачи необходимо определить величину платежа постоянного р- срочного ограниченного аннуитета постнумерадо.
По условию задачи:
FVpst = 10 000 руб., p = 4, r = 0,12, m=4.
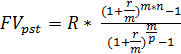 ,
,
R = 10 000 * 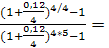 372,16 руб.
372,16 руб.
Таким образом, ежеквартальный взнос должен составлять 372,16 руб.
3. Какой необходим срок для накопления 60 тыс. руб. при условии, что ежегодно вносится по 10 тыс.руб. по схеме постнумерандо, а на накопленные фонды начисляются проценты по ставке 9 % годовых.
Необходимо определить срок постоянного годового аннуитета постнумерандо.
По условию задачи FVpst = 60 000 руб., R = 10 000 руб., r = 0,09.
n = 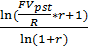 =
= 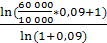 = 5 лет
= 5 лет
Следовательно, срок аннуитета должен составлять 5 лет.
4. Господин В. вкладывает 25 000 рублей в начале каждого года в банк, выплачивающий проценты по ставке 8% годовых с ежеквартальным начислением (сложные). Какая сумма будет на счету Петрова через 4 года.
Необходимо определить будущую стоимость постоянного годового ограниченного аннуитета пренумерандо.
По условию задачи R = 25 000 руб.. n = 4 года, r = 0,08, m = 4.
а) FVpre = 25 000 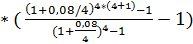 = 122377,96 руб.
= 122377,96 руб.
или
б) FVpre = FVpst* 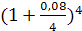
FVpre = 25 000* 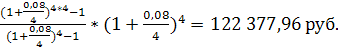
5. Определите будущую и современную стоимость переменного потока платежей на основе следующих данных:
| Год | ||||
| Платеж, руб. | ||||
| Ставка, % |
Осуществите расчет для двух вариантов:
а) платежи производятся в конце периода,
б) платежи производятся в начале периода.
Необходимо рассчитать будущую и современную стоимость переменного годового ограниченного аннуитета.
По условию R1 = 100руб., R2 = 150руб, R3 = 20руб, R4 = 370руб., r = 0,1, n= 4 года.
а) определим стоимость постнумерандо
FVpst =
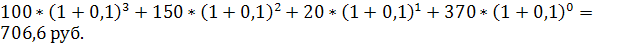
PVpst =
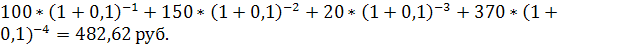
б) определим стоимость пренумерандо
FVpre =
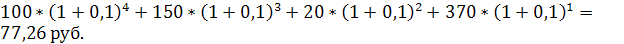
Ppre = 100 +
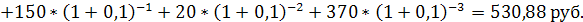
6. Определите, какую сумму необходимо положить в банк, чтобы в течение следующих 5 лет иметь возможность снимать со счета каждый год по 100 тыс. руб. по схеме постнумерандо, исчерпав весь счет к концу этого срока, если банк начисляет проценты по ставке 10 % годовых (сложные).
Необходимо определить современную стоимость постоянного годового ограниченного аннуитета постнумерандо.
По условию задачи R = 100 000 руб., n = 5 лет, r = 0,1.
PVpst = 100 000 * 
Следовательно, сегодня необходимо разместить на счете 379 078,68 руб.
7. Определите современную стоимость аннуитета постнумерандо продолжительностью 5 лет, который не предполагает никаких поступлений в первые два года и равные поступления в 1000 рублей в оставшиеся годы, если ставка составляет 5% годовых для первых двух лет и 8% годовых для оставшихся трех лет.
Необходимо определить современную стоимость постоянного годового ограниченного аннуитета постнумерандо.
Особенность данного потока состоит в том, что момент начала выплат не совпадает с началом срока аннуитета. Такой аннуитет называется отложенным или отсроченным.
По условию задачи R = 1000 руб., n1 = 2 года, n2 = 3 года, r1 = 0,05, r2 = 0,08.
Рассчитаем стоимость потока на момент начала выплат:
PVpst = 1000 * 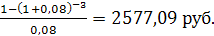
Для получения современной стоимости потока необходимо полученную стоимость привести к моменту оценки:
PVpst = 2577,09* 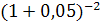 = 2337,5 руб.
= 2337,5 руб.
8. Рассчитайте текущую стоимость бессрочного аннуитета с ежегодным поступлением 100 руб. в конце каждого года при годовой процентной ставке 10%.
Необходимо определить современную стоимость бессрочного годового аннуитета постнумерандо.
По условию задачи R = 100 руб.,r = 0,1.
PVpst = 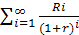 =
= 
Следовательно, современная стоимость вечного аннуитета составит 1000 руб.
9. Потребительский кредит в сумме 25 000 руб. выдан на два года при разовом начислении процентов по ставке 10% годовых (простые проценты). Погашение задолженности помесячное. Определите остаток долга на начало 4 месяца, а также проценты по нему.
В данной схеме погашения потребительского кредита проценты, как правило, начисляются на всю сумму кредита и присоединяются к основному долгу уже в момент открытия кредита. Погашение долга с процентами производится равными суммами на протяжении всего срока кредита. Воспользуемся для решения задачи наиболее простым методом - равномерное распределение выплат процентов.
По условию задачи P = 25 000 руб., n = 2 года, p = 12, r = 0,1.
Определим наращенную сумму долга
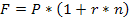
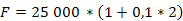 = 30 000 руб.
= 30 000 руб.
Рассчитаем величину разового погасительного платежа
R 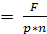
R = 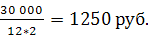
R состоит из расходов на уплату сумму процентов (R1) и на погашение долга (R2):
R= R1 + R2
R1 = 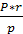 =
= 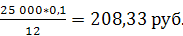
R2 = 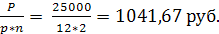
Остаток долга на начало 4 месяца: D4 = P - R2(1-3)
D4 = 25000-1046.67=21874.99руб.
Проценты к уплате по истечении 3 месяцев:
I = 21*208.33=4374,93 руб.
Схема погашения кредита представлена в таблице.
| Месяц | Остаток ссуды на начало месяца | Сумма платежа за месяц | В том числе | Остаток ссуды на конец месяца | |
| Проценты за месяц R1 | Погашенная часть долга R2 | ||||
| 208,33 | 1041,67 | 23958,33 | |||
| 23958,33 | 208,33 | 1041,67 | 22916,66 | ||
| 22916,66 | 208,33 | 1041,67 | 21874,99 | ||
| 21874,99 | 208,33 | 1041,67 | 20833,32 | ||
| … | |||||
| 1041,67 | 208,33 | 1041,67 |
10. Под залог недвижимости выдана ссуда в размере 240 000 рублей на 10 лет. Погашение осуществляется ежемесячно по схеме постнумерандо. На долг начисляются проценты по ставке 12% годовых ежемесячно. Определите ежемесячные расходы должника, а также остаток долга на начало 3 месяца.
Для решения данной задачи воспользуемся условиями стандартной ипотечной ссуды. Она предполагает равные ежемесячные взносы по схеме постнумерандо.
По условию задачи:
PVpst = 240 000 руб., r = 0,12, m = 12, n = 10 лет, p = 12.
Определим величину ежемесячного платежа
R = 240 000 * 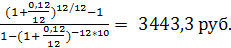
R состоит из расходов на уплату сумму процентов (R1) и платежей в погашение долга (R2):
R= R1 + R2
R1 за 1 месяц = 240 000 * 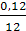 = 2400 руб.
= 2400 руб.
R2 за 1 месяц = 3443,3 – 2400 = 1043,3 руб.
Остаток долга на конец 1 месяца D1= 240 000 -1043,3 = 238965,7 руб.
Схема погашения ссуды отражена в таблице.
| Месяц | Остаток ссуды на начало месяца | Сумма платежа за месяц | В том числе | Остаток ссуды на конец месяца | |
| Проценты за месяц | Погашенная часть долга | ||||
| 240 000 | 3443,3 | 1043,3 | 238956,7 | ||
| 238956,7 | 3443,3 | 2389,57 | 1053,73 | 237902,97 | |
| 237902,97 | 3443,3 | 2379,03 | 1064,27 | 236838,7 | |
| … | |||||
| 3409,2 | 3443,3 | 34,10 | 3409,2 |
Остаток долга на начало третьего месяца можно определить и на основе следующей формулы:
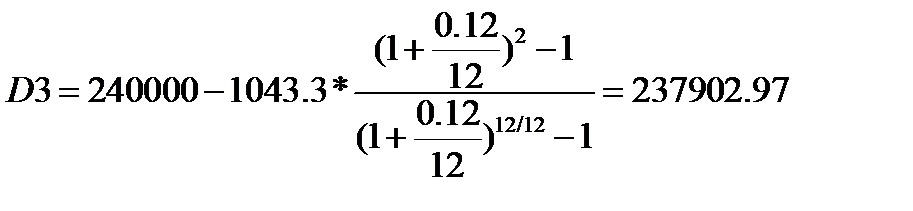
11. Предполагается в конце каждого полугодия снимать со счета 8000 рублей и в конце 4 года исчерпать счет полностью. Банк должен начислять проценты по ставке 12% годовых с ежеквартальным начислением. Какую сумму можно снимать со счета ежеквартально, если проценты будут начисляться ежемесячно?
По условию задачи постоянный аннуитет постнумерандо характеризуется следующими параметрами р = 2, R = 8000, n = 4, r = 0,12 при m = 4. Необходимо определить величину платежа заменяющей ренты, у которой р = 4, n =4, r = 0,12 при m =12.
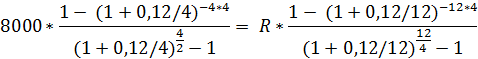
49501.88 = R * 12.532
R = 3949.96 руб.
Со счета можно снимать ежеквартально 3949,96 руб., если проценты будут начисляться ежемесячно.
12. Постоянный аннуитет постнумерандо сроком 4 года откладывается на 2 года без изменения величины ежегодного платежа. Определите новый срок аннуитета при ставке сложных процентов 20% годовых.
По условию задачи постоянный аннуитет постнумерандо характеризуется следующими параметрами R, n = 4, r = 0,2. Необходимо определить срок заменяющей ренты (отсроченный или отложенный аннуитет): R 2 = R1, r 2 = r1 = 0,2, эти параметры не меняются. n2 -?
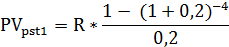
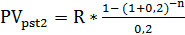 *(1+0,2)-2
*(1+0,2)-2
Приравняем современные стоимости двух рент: 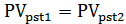
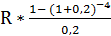 =
=  *(1+0,2)-2
*(1+0,2)-2
Рассчитаем срок новой ренты: 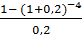 =
= 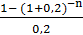 *(1+0,2)-2
*(1+0,2)-2
n2 = 7,5 (г.)
| <== предыдущая страница | | | следующая страница ==> |
| Потоки платежей и их оценка | | | Тестовые задания. 1. Коэффициент приведения ренты зависит от |
Дата добавления: 2014-11-04; просмотров: 4067; Нарушение авторских прав

Мы поможем в написании ваших работ!