Задачи с решением

1. Предоставлена ссуда 60 000 рублей 16 января с погашением через 9 месяцев под 18% годовых (год невисокосный). Рассчитайте сумму к погашению при различных способах начисления процентов:

а) обыкновенные проценты с точным числом дней;

б) обыкновенные проценты с приближенным числом дней;

в) точные проценты с точным числом дней.

В данной задаче применяется простая ставка r = 0,18; исходный капитал составляет P=60 000 руб.; точное число дней ссуды = 273дня (определяется по календарю), приближенное число дней = 30 дней * 9 месяцев = 270 дней.

Определяем будущую стоимость по формуле:

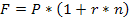
А) F=60 000*(1+0,18* 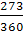) = 68190 руб.

Б) F=60 000*(1+0,18* 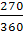) = 68100 руб.

В) F=60 000*(1+0,18* 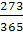) = 68077,81 руб.

Таким образом, использование различных способов расчета процентов приводит к разным значениям будущей стоимости.

2. На депозит в банке были размещены 100 000 руб. Через 2 года 6 месяцев на счете было 120 000 руб. Определите, какую процентную ставку простых процентов использует банк.

В задаче имеются будущая F = 120 000 руб. и современная P = 100 000 руб. стоимости, срок сделки n=2,5 года (при использовании обыкновенных процентов с приближенным числом дней сделки). Для расчета воспользуемся следующей формулой:

.

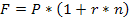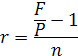
r = [(120 000/100 000)-1]/2,5=0,08

Таким образом, процентная ставка составляет 8%.

3. Банк предоставил ссуду в размере 10 000 руб. на два года на следующих условиях: за первый год плата за ссуду будет исчисляться исходя из простой процентной ставки 10% годовых, в каждом последующем полугодии процентная ставка будет возрастать на 5%. Определите, какую сумму должен вернуть заемщик.

В задаче указана исходная сумма денег P = 10 000 руб., значение процентной ставки меняется, поэтому r₁ = 0,1, n₁ = 1 год, r₂ = 0,15, n₂ = 0,5 года, r₃= 0,2, n₃ = 0,5 года. Совокупный срок для начисления процентов в соответствии с условиями задачи составит 2 года. Поскольку ставка является переменной, необходимо внести изменения в основную формулу:

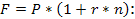
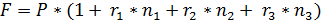
F = 10 000 * (1+0,1*1 +0,15*0,5 +0,2*0,5) = 12750 руб.

Заемщик должен вернуть 12750 рублей.

4. Предоставлена ссуда в размере 8 000 рублей на 2 года. Определите, какую сумму необходимо вернуть должнику, если сложная процентная ставка составляет 15% годовых.

Определим исходные данные для расчета:

P = 8000 руб., r = 0,15, n = 2 года.

Воспользуемся формулой:

.

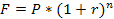F = 8000*(1+0,15)² = 10580 руб.

Должнику необходимо вернуть через два года 10580 рублей.

5. Банк начисляет проценты по вкладам по ставке 6% годовых (сложные). Определите эффективную ставку по вкладам, эквивалентную номинальной, если начисление процентов производится а) по полугодиям, б) поквартально, в) ежемесячно.

В условии задачи представлена номинальная сложная процентная ставка

r_ном = 0,06, на основе которой производится начисление процентов

а) по полугодиям, следовательно, m = 2,

б) поквартально, m = 4,

в) ежемесячно, m= 12. Срок сделки не указан, по умолчанию n = 1.

Для определения эффективной ставки применим формулу

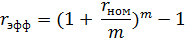
а) 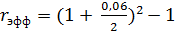= 0,0609

б) 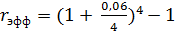= 0,0614

в) 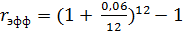= 0,0617

Получаем следующие эквивалентные ставки: использование ставки 6% годовых с полугодовым начислением позволит получить тот же результат по окончании сделки, что применение ставки 6,09 % годовых; использование ставки 6% годовых с ежеквартальным начислением позволит получить тот же результат по окончании сделки, что применение ставки 6,14 % годовых; использование ставки 6% годовых с ежемесячным начислением позволит получить тот же результат по окончании сделки, что применение ставки 6,17 % годовых. Таким образом, с увеличением внутригодовых начислений значение годовой эффективной ставки увеличивается.

6. Предприятие получило в сумме 34650 руб. Через 2 года по условиям договора заемщик должен вернуть 51 650 руб. Определите ставку за кредит, если начисление процентов производится ежеквартально (сложные).

По данным задачи P = 34650 руб., F = 51 650 руб., m = 4, n = 2. Рассчитаем сложную процентную номинальную ставку:

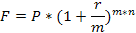
Отсюда, 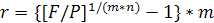= 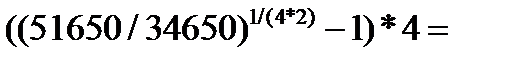0,205

Таким образом, сложная номинальная процентная ставка составит 20,5% годовых.

7. Определите срок, через который 100 руб., размещенные в кредитной организации вырастут до 6605 руб., если ставка сложных процентов составляет 10% при ежемесячном начислении процентов.

На основе представленных данных определим необходимые для расчета условия сделки: P = 100 руб., F = 6605 руб., r = 0,1, m = 12.

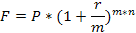
Отсюда, r = 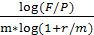= =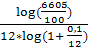42 года.

Следовательно, для получения капитала в 6605 при наличии 100 рублей необходимо 42 года при условии начисления процентов по ставке 10% годовых с ежемесячной капитализацией.

8. Банк предоставил ссуду в размере 20 000 руб. на два года на следующих условиях: за первый год плата за ссуду будет исчисляться исходя из сложной процентной ставки 10% годовых, в каждом последующем полугодии процентная ставка будет возрастать на 5%. Определите, какую сумму должен вернуть заемщик.

Данные для решения задачи: P = 20 000 руб., r₁ = 0,1, r₂=0,15, r₃= 0,2,

n₁= 1 год, n₂ = 0,5 года, n₃ = 0,5 года.

Совокупный срок сделки в соответствии с условиями задачи составит 2 года. Ставка, представленная в задаче, является переменной, поэтому необходимо внести изменения в формулу:

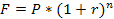
F = P *( 1+ 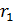)ⁿ₁ * (1+ 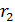)ⁿ₂ *(1+ 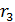)ⁿ₃

F = 20 000 *( 1+0,1)¹ * (1+0,15)^0,5 *(1+0,2)^0,5 = 26886,45 руб.

Заемщик должен вернуть через два года 26886,45 руб.

9. На сумму 25 000 рублей в течение трех месяцев начислялись простые проценты по ставке 14% годовых. За каждый месяц цены росли на 1,1;1,2 и 1,3%. Определите наращенную сумму с учетом инфляции и величину положительной процентной ставки.

Данные для решения задачи: P = 25 000 руб., r = 0,14, n= 0,25 года, h₁ = 0,011,

h₂ = 0,012, h₃ = 0,013.

Для решения задачи необходимо определить индекс цен за три месяца. Воспользуемся формулой со сложной процентной переменной ставкой:

Jp=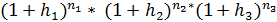

Темп инфляции используется в расчетах как периодическая ставка.

Jp = (1+0,011)*(1+0,012)*(1+0,013)= 1,0364

Fi=P*[(1+r_d*n)/Jp] = 25 000*[(1+0,14*0,25)/1,0364]= 24966,23 руб.

Рассчитаем барьерную ставку:

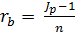
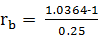= 0,1456

Наращенная сумма с учетом инфляции составит 24966,23 руб., положительная ставка – это ставка, превышающая барьерную, т.е. более 14,56%.

10. Банк выдает клиенту кредит на 3 месяца, в течение которых по оценкам экспертам ежемесячный индекс инфляции составит 1,01. Определите значение процентной сложной ставки, полностью компенсирующей потери от инфляции, если банк желает обеспечить реальную доходность, определяемую сложной процентной ставкой в 5% годовых.

По данным задачи r_s= 0,05, Jp(мес) =1,01, n = 0,25.

Рассчитаем брутто-ставку:

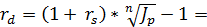
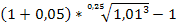= = 0,18317

Таким образом, при ежемесячном индексе цен 1,01 банк должен установить брутто-ставку 18,317% для обеспечения реальной доходности 5%.

11. Банк предлагает клиентам помещать деньги на депозит на один год 8% годовых с ежеквартальным начислением сложных процентов. Определите реальную доходность такого предложения для клиентов банка, если ежемесячный индекс инфляции прогнозируется равным 1,011.

По условию задачи r_d= 0,08, m =4, Jp(мес)=1,011.

Jp = 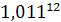=1,1403

Возможны два варианта решения данной задачи:

а) Необходимо определить величину эффективной ставки, эквивалентной номинальной ставке r = 0,08 при m = 4:

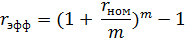
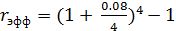= 0.0824

Затем рассчитать реальную эффективную процентную ставку:

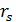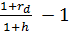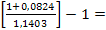= = -0,0508

Следовательно, реальная доходность составляет -5,08%.

б) Необходимо использовать множители наращения с номинальной ставкой:

( )/Jp =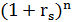

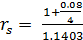- 1 = -0.0508

Следовательно, реальная доходность составляет -5,08%.

При необходимости можно определить и величину реальной номинальной ставки с ежеквартальным начислением процентов. Для этого вновь будет применен принцип эквивалентности ставок.

12. На вклад в 100 000 рублей ежемесячно начисляются проценты по сложной процентной ставке 12% годовых. Оцените сумму вклада через 2 года с точки зрения покупательной способности, если ожидаемый темп инфляции 1% в месяц. Определите величину положительной процентной ставки.

По условию задачи:

F = 100 000 руб., r_d = 0,12, m = 12, h (мес.)= 0,01, n = 2 года.

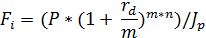
Определим на основе данной формулы будущую стоимость с учетом инфляции:

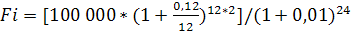= 100 000 руб.

Следовательно, стоимость денежных средств с учетом инфляции не изменится. Ставка, обеспечивающая сохранение денежных средств в первоначальном размере с учетом инфляции, является барьерной. Cтавка r = 0,12 при m = 12 является барьерной, и любая ставка больше нее будет положительной.

13. Какую сумму надо положить в банк, выплачивающий 4% простых в год, чтобы получить 52 000 руб. через 1 год?

По условию задачи F = 52 000 руб., r = 0,04, n = 1 год.

Для решения используем математическое дисконтирование:

P=F/(1+r*n)

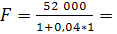50 000 руб.

На счете сегодня необходимо разместить 50 000 для получения через год 52 000 руб. при использовании простой процентной ставки 4% годовых.

14. Через три года от настоящего момента вы планируете поменять автомобиль, потратив на эту операцию 550 000 рублей, также через год от настоящего момента вы желаете отправиться на отдых, потратив 90 000 рублей. Определите, какую сумму необходимо разместить на счете сегодня, для накопления желаемых сумм, если банк предлагает 10% годовых (сложные).

По условию задачи F₁ = 90 000 руб., F₂= 550 000 руб., n₁ = 1 год, n₂ = 3 года, r = 0,1.

Применим для решения задачи математическое дисконтирование:

P=F/(1+r)ⁿ

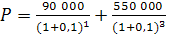= 81818,18 + 413223,14 = 495041,32 руб.

При определении современной стоимости будущих трат нельзя забывать о невозможности суммирования денежных средств, относящихся к разным моментам времени. Для устранения этого препятствия, приведем обе суммы к текущему моменту времени, затем их складываем. Таким образом, для совершения запланированных в будущем расходов, необходимо разместить сегодня на счете 495041,32 руб. при условии начисления процентов по сложной процентной ставке 10% годовых.

15. Вексель на сумму 10 000 рублей, срок платежа по которому наступает через полгода, продан с дисконтом по простой учетной ставке 15% годовых. Какова сумма дисконта?

По условию задачи F = 10 000 руб., n = 0,5 года, d = 0,15.

Воспользуемся для решения задачи банковским дисконтированием:

P=F*(1-d*n)

P=10 000*(1-0,15*0,5)= 9250 руб.

D=F-P = 10000 – 9250 = 750 руб.

Дисконт составит 750 руб.

16. Господин А. имеет вексель на 15 000 руб., срок погашения которого наступает 1 июля. Он желает его учесть в банке 1 марта того же года. Какую сумму получит господин А., если банк использует простую учетную ставку 7% годовых?

По условию задачи F = 15 000 руб., d = 0,07, n = 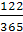года. n определяется как временной интервал между моментом учета векселя в банке и моментом его погашения.

P=F*(1-d*n) = 15 000 * (1-0,07* 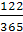)= 14649,04 руб.

В результате учета векселя господин А. получит 14 649,04 руб.

17. Господин А. занял у господина В. деньги, получив от него 9800 рублей и выдав ему вексель, по которому обязался выплатить 10 000 рублей через 3 месяца. Под какую годовую учетную ставку (простые проценты) выдан этот вексель?

По условию задачи F = 10 000 руб., P = 9800 руб., n = 0,25 года.

Воспользуемся для решения задачи банковским дисконтированием:

P=F*(1-d*n)

=

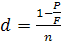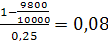
Таким образом, вексель был выдан под простую учетную ставку 8%.

18. Кредит предоставляется под 18% сложных процентов сроком на 10 лет. Господин В., получающий кредит, желает привлечь его под простые проценты (на ту же сумму на тот же срок). Определите ставку простых процентов, которая должна быть предусмотрена контрактом.

По условию задачи r₁ = 0,18, n₁ = 10 лет, n₂ = 10 лет.

Воспользуемся принципом эквивалентности ставок:

(1+r₂*n₂)= (1+r₁)ⁿ₁

Отсюда, r₂ = 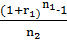= = 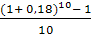0,4234

Следовательно, простая процентная ставка составит 42,34% годовых.

19. Платежи в размере 10 000 рублей и 20 000 рублей со сроками уплаты один и два года объединяются в один со сроком один год 6 месяцев. При консолидации платежей применяется сложная ставка 10% годовых. Определите величину консолидированного платежа.

В данном случае используется наращение для первого платежа, срок сделки составляет 6 месяцев, а для второго платежа – дисконтирование, срок тот же.

F = 10000*(1+0.1)^0.5=10488.09 руб.

P = 20000*(1+0.1)^-0.5 = 19069.25 руб.

Оба платежа приведены к одному моменту времени, возможно их суммирование.

10488,09+19069,25=29557,34 руб.

20. Определите, являются ли эквивалентными следующие обязательства: первое – выплата 15 000 рублей через 3 месяца, второе - 18 000 рублей через 6 месяцев. Для сравнения используйте простую ставку 8% годовых.

Для решения задачи используем дисконтирование и приведем оба обязательства к текущему моменту времени, что сделает их сопоставимыми.

Р = 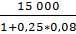= 14 705,88 руб.

Р = 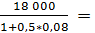17307,69 руб.

Обязательства при ставке 8% годовых не эквивалентны друг другу.

Дата добавления: 2014-11-04; просмотров: 3457; Нарушение авторских прав

Мы поможем в написании ваших работ!