Виды динамических зконометрических моделей

Раздел 4. Динамические эконометрические модели

Шаг 3

Шаг 2

Шаг 1

Пример

Двухшаговый МНК

Этот метод применяется в случае сверх идентифицируемых моделей и заключается в том, что:

1. Составляется приведённая модель и оцениваются приведённые коэффициенты.

2. Выявляются эндогенные переменные в кривой структурного уравнения, параметры которого определяют с помощью двухшагового МНК, и рассчитываются значения этих эндогенных переменных по приведённым уравнениям.

3. С n-ого МНК определяются структурные коэффициенты в сверх идентифицируемых уравнениях, используя в качестве исходных данных фактические значения экзогенных переменных, определённые на втором шаге. Коэффициенты в идентифицированных структурных уравнениях определяются, как и в классическом МНК.

Пусть структурная модель имеет вид:

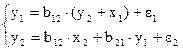
В данной системе второе уравнение идентифицируемое, а первое – сверхидентифицируемое, т.к.

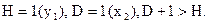
Приведённая форма модели имеет вид:

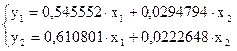
Выявление эндогенной переменной в правой части сверх идентифицированного первого уравнения. Это .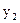

Рассчитаем значение 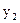_, исходя из приведённого уравнения, и определим значение суммы .

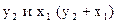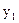
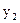
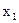
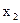
Номер наблю-дения					y2 (расч. по привед. урав.)		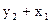y1 (расч. по привед. урав.)
	-1,185	9,97	1,99	-30,55	-8,792	-6,8	-0,792
	-0,385	-7,93	-3,21	-9,55	1,0837	-2,126	-0,45664
	-1,385	-16,83	1,59	-49,55	-12,622	-11,03	-1,37397
	-1,435	-14,03	-12,11	-23,35	6,91	-5,2	-1,34897
	0,515	-0,33	4,89	32,45	2,335	7,225	1,223366
	-0,785	-5,73	-11,11	23,05	16,242	5,132	0,073427
	2,015	13,67	19,19	49,45	-8,18	11,01	2,50461
	-0,485	-3,43	3,19	12,05	-0,5071	2,683	0,529248
	4,815	43,67	11,09	65,45	3,4823	14,572	2,53441
	-1,685	-19,03	-15,51	-69,45	0,0471	-15,463	-2,89345

Определим структурные коэффициенты в первом уравнении, применив непосредственно МНК для их нахождения: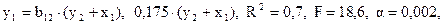т.е. модель существенна. Здесь в качестве 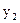используем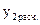

Структурные коэффициенты в идентифицируемом уравнении определяются обычным образом, как в классическом МНК, считая .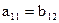

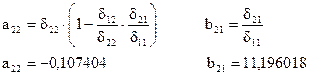
В целом получим:

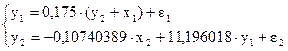
Эконометрические модели, построенные по данным, характеризующим какое-либо явление в различные моменты или периоды времени, называются динамическими.

К динамическим моделям относятся:

§ одномерные временные ряды:

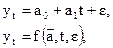
например,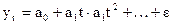

В случае одномерных временных рядов либо неизвестны, либо игнорируются факторы, от которых зависит результирующий признак, за исключением фактора времени, например, изменение валютного курса во времени, когда влияющих факторов очень много, но их действие либо трудно учесть, либо плохо предсказуемо;

§ временные ряды с детерминированной формой зависимости результатного признака от известных факторов:

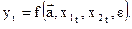Например,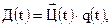

где 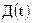- объем реализации в денежном выражении (доходы), 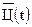- средние цены реализации, 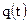- объем реализации в натуральном выражении. В этом случае зависимость 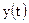целиком определяется зависимостями факторов, входящих в модель, от времени:

§ временные ряды со стохастической зависимостью результатного признака от факторов. Предыдущий случай является частным случаем данного. При этом ошибка определяется не только ошибками зависимости факторов от времени, но и ошибками от стохастической связи результатного признака от факторных признаков;

§ лаговые динамические модели, в которых результатный признак зависит не только от значений факторных признаков в соответствующий промежуток (момент) времени, но и от значений факторов в предыдущие промежутки (моменты) времени, т.е. ;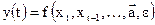

§ авторегрессионные динамические модели, в которых результатный признак зависит не только от времени и значений факторных признаков, но и от значений результатного признака в предыдущие промежутки (моменты) времени. По существу, простая модель такого рода – это иное описание одномерного ряда. Пусть зависимость одномерного ряда от времени описывается как .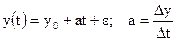

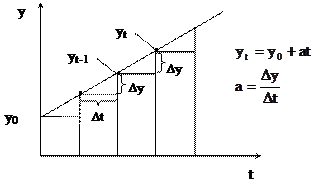Иначе можно записать эту зависимость в виде авторегрессионной модели: ,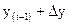

где при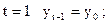

§ наиболее сложные динамические модели – это системы динамических эконометрических уравнений.

Дата добавления: 2014-03-19; просмотров: 464; Нарушение авторских прав

Мы поможем в написании ваших работ!