Главная страница Случайная лекция
Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика
Мы поможем в написании ваших работ!
Системы эконометрических уравнений. Достаточное условие идентификации структурной
Достаточное условие идентификации структурной
Более точно условия идентификации определяются, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нём переменным (экзогенным и эндогенным) можно из коэффициентов при этих переменных в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных системы без единицы.
Рассмотрим структурную модель (число эндогенных переменных равно 3, экзогенных - 4):
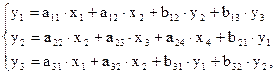
следовательно,
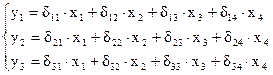
Проверим каждое уравнение на необходимое и достаточное условие идентификации.
Для первого уравнения
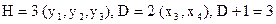– необходимое условие идентификации выдержано.
Для проверки на достаточное условие идентификации заполним следующую таблицу коэффициентов при соответствующих в первом уравнении переменных:
| Уравнение | Переменные | |
| x3 | x4 | |
| a23 | a24 |
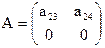
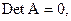следовательно, уравнение идентификации выполняется, и первое уравнение нельзя считать идентифицируемым.
Для второго уравнения
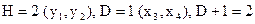, т.е. уравнение идентифицируемо. Достаточное условие идентификации выполняется. Коэффициенты при отсутствующих во втором уравнении переменных составят:
| Уравнение | Переменные | |
| y3 | x1 | |
| b13 -1 | a11 a31 |
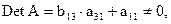ранг матрицы равен 2, т. е. равен числу эндогенных переменных без 1, что соответствует критерию: ранг матрицы коэффициентов должен быть не менее чем число эндогенных переменных в системе без одного. Следовательно, второе уравнение точно идентифицируемо.
Для третьего уравнения системы
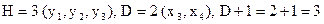и необходимому условию идентификации оно соответствует.
Однако составим таблицу коэффициентов при отсутствующих в третьем уравнении переменных:
| Уравнение | Переменные | |
| x3 | x4 | |
| a23 | a24 |
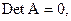т.е. достаточное условие идентификации не выполняется. Уравнение идентифицируемо.
Следовательно, рассматриваемая в целом структурная модель, идентифицируемая по счётному правилу, не является идентифицируемой, исходя из достаточного условия идентификации.
Кроме рассмотренных условий идентифицируемости на структурные коэффициенты модели могут накладываться и другие ограничения: на дисперсии и т.д.
| <== предыдущая страница | | | следующая страница ==> |
| Формы системы эконометрических уравнений | | | Виды динамических зконометрических моделей |
Дата добавления: 2014-03-19; просмотров: 374; Нарушение авторских прав
Мы поможем в написании ваших работ!