Глава 5 Использование теории вероятности и математической статики для построения математических моделей производственных процессов

Случайная величина – величина, которая в результате опытов может принимать то или иное значение.

Вероятность события – численная мера объективных возможностей этого события. Существует понятие относительной частоты события, которое определяется как отношение числа случаев 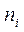, благоприятствующие событию i ко всем наблюдаемым случаям n. В этом случае говорят:

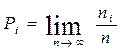
Случайная величина считается полностью заданной, если известен закон ее распределения. Законом распределения называется соотношение между возможным значением случайной величины и соответствующим им вероятностям. Простейшей формулой закона распределения является таблица:

			...
			…

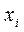
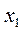
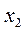
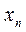
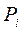
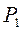
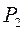
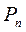
Пусть есть случайная величина х. Вероятность того события, что случайная величина примет значение Р (Х<х) называется функцией распределения случайной величины:

Р (Х<х) = F(х)

График распределения случайной величины:

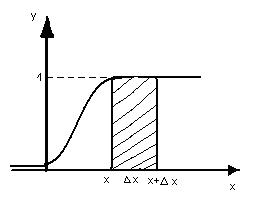
Вероятность попадания случайной величины на заданном участке 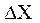равна приращению функции распределения, т.е.

,

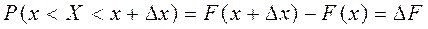тогда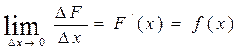

f(x) называется функцией плотности распределения. Поэтому вероятность попадания в элементарный промежуток 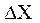равна:

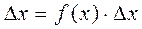
а вероятность попадания случайной величины в промежуток от 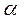до 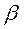равна:

Связь функции распределения с функцией плотности распределения задается формулой:

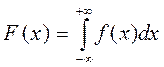
Свойства функции плотности распределения.

Функция плотности распределения имеет следующие свойства распределения:

1. Функция всегда положительна:

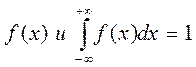
2. Функция f(х) имеет размерность обратную размерности случайной величины.

Построение графика функции плотности распределения по результатам эксперимента.

Для построения функции строиться гистограмма.

Гистограмма – некий статистический ряд величин, оформленный графически.

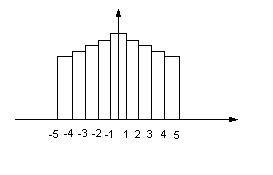Для построения гистограммы на оси абсцисс откладывают интервалы изменения случайной величины, и на каждом интервале, как на основании строиться прямоугольник. Причем площадь каждого прямоугольника равна относительной частоте данного ряда. Для построения гистограммы, нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника. Полученный график будет представляет собой плотность распределения f(x) случайной величины х.

Интервалы для построения гистограммы выбирают произвольно, но для определения оптимальной величины интервала применяют формулу:

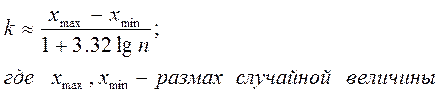
В качестве основных характеристик случайной величины являются:

· математическое ожидание;

· дисперсия;

· асимметрия;

· эксцесс (плотность распределения Ф(х) случайной величины).

Математическим ожиданием случайной величины называется сумма произведений 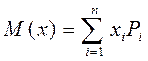. С другой стороны математическое ожидание может оцениваться как среднее значение этой величины, равное: 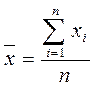(для достаточно больших n). Из этого следует, что

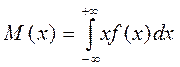(для непрерывных случайных величин).

Свойства математического ожидания

· Математическое ожидание постоянной величины равняется самой постоянной величине: М(с)=с

· М(сх)=СМ(х)

· М(х+у)=М(х)+М(у)

· М(х,у)=М(х)М(у)

Дисперсией (рассеванием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

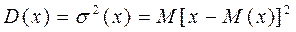
где х-М(х) – отклонение случайной величины х от ее среднего значения М(х). Соответственно дисперсия – это среднее значение квадрата отклонения случайной величины от ее среднего значения.

Для дискретной величины дисперсия:

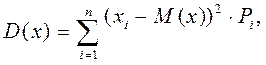
а для непрерывных случайных величин:

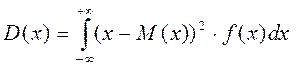
Свойства дисперсии:

· D(c)=0

·

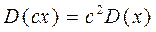
· D(x+y)=D(x)+D(y)

· D(x*y)=D(x)D(y)

·

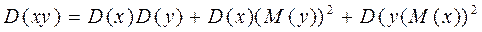
Асимметрия – характеристика, служащая для определения сложности распределения.

Рассчитывается: для дискретных случайных величин

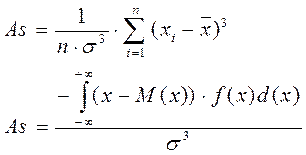
Для определения характеристики крупности, применяют формулу:

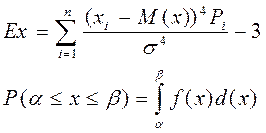
f(x) – функция плотности распределения.

Законы распределения случайной величины.

Нормальный закон распределения имеет вид:

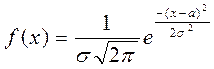
Нормированным называется распределение у которого а=0, 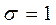. Нормирование достигается путем внедрения новых переменных.

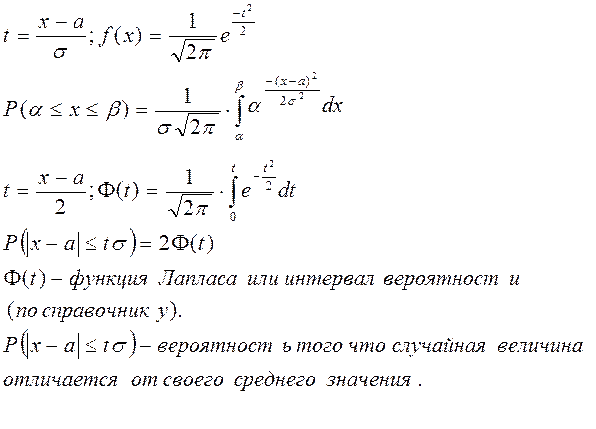
Ф(-t) = -Ф(t)

Вероятность попадания случайной величины в интервал (t1;t2) в случае, если эта случайная величина распределена по нормальному закону:

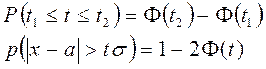
Для анализа этого распределения, которые мы получили экспериментально, к нормальному закону используют критерии согласия (Стьюдента).

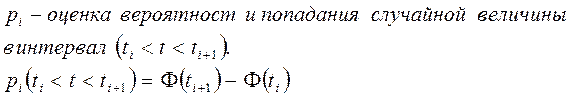Наибольшее значение 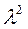(км) сравнивается с табличными значениями по числу степени свободной величины 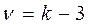и экспериментально;

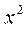- находим вероятность того что рассмотренные различия экспериментального и нормального распределения, малое значение величины Ф соответствует малой вероятности случайного отклонения и следовательно, о наличие систематического отклонения от нормального закона.

Нормальный закон распределения случайной величины имеет место тогда когда исходные представляют собой сумму независимых переменных величин, дисперсии которых малы по сравнению с дисперсией суммы.

Закон равномерной плотности распределения

Все случайные величины, снимаемые в эксперименте, будут попадать в интервал (а; в).

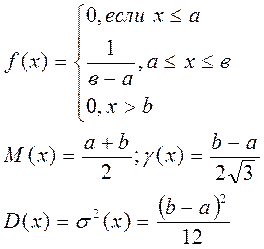
Показательный (экспериментальный) закон распределения имеет вид:

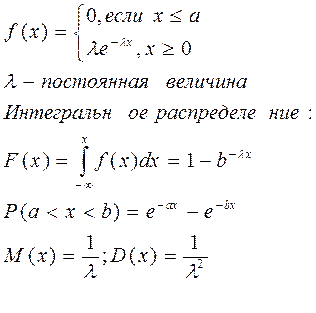
важный вывод:

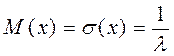- это условие, которое следует проверить, что случайная вероятность распределена по такому закону.

Часть длительности времени. Безотказность результата имеет показатель распределения.

Интегральная функция распределения:

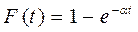
Вывод: чем > эксперимент авто тем быстрее он выйдет из строя.

Час показательного распределения имеет вид:

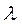- интенсивность отказа Z. Если на практике исследовать параметр 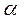, то при отсутствии данных о 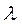используют его арифметическое среднее, т.е.

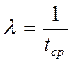
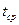- среднее время безотказности результативности авто.

Понятие о корреляционном и регрессионном анализе.

Две случайные величины являются корреляционно связанными, если математическое ожидание одной из них изменяется в зависимости от изменения другой величины. Выборочный коэффициент линейной корреляции:

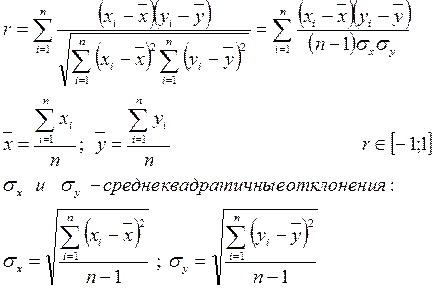
Недостаток коэффициента корреляции - его применимость для оценки степени связности между собой линейной зависимостью случайных величин.

Метод выравнивания функций позволяет значительно расширить возможности коэффициента корреляции для оценки степени взаимозависимости двух случайных величин связанных между собой не линейными зависимостями. Линейную связь обычно считают слабой если:

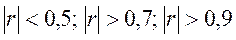
Взаимосвязь между случайными и неслучайными величинами называется регрессионной, а методы анализа изучения – регрессионным анализом.

Уравнение линейной регрессии как функции y(x) записывается в виде:

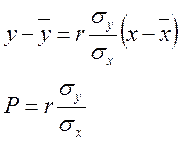
Глава 6. Решение производственных задач на основе компьютерных моделей принятия решений.

§ 6.1 Алгоритм принятия решений.

Как было указано в предыдущих разделах монографии, компьютерные модели востребованы для принятия основных технических решений при проектировании предприятий, управлении их производственной деятельностью (в том числе и планировании технико-экономических показателей) и при организации работ на предприятии. Вместе с тем, наличие на предприятии возможности приобретения или разработки КСПР, не всегда является достаточным условием повышения эффективности производства. Как уже указывалось в главе 6, необходимо иметь возможность предварительно оценивать экономический эффект от внедрения и эксплуатации КСПР. В свою очередь, для получения такой оценки необходим инструмент прогнозирования последствий от реализации принятых решений с помощью КСПР. Также, необходим выверенный алгоритм решения производственных проблем с помощью методов компьютерного моделирования.

Ниже представлен алгоритм принятия решений в производственных задачах на основе использования компьютерных моделей. Данный алгоритм построен на основе обобщения результатов исследований, описанных в предыдущих главах.

 

1. Формулировка производственной проблемы, подлежащей разрешению.

2. Определение цели, которая должна быть достигнута в результате решения производственной задачи и выбор критерия (критериев) оптимизации.

3. Оценка возможного экономического эффекта от практической реализации принятого решения.

4. Оценка затрат на принятие решения и реализацию его на практике.

5. Определение лица ответственного за принятие и реализацию решения и лиц, участвующих в разработке мероприятий обеспечивающих принятие решения.

6. Выбор и подготовка исходных данных.

7. Разработка методики численного эксперимента с использованием компьютерной модели.

8. Подготовка дополнительных исходных данных, необходимых (недостающих) для проведения численного эксперимента.

9. Анализ полученных результатов, выбор оптимального (окончательного) решения, лицом ответственным за принятие решения.

10. Прогноз последствий от практической реализации принятого решения (оценка последствий от реализации принятого решения).

11. Преобразование информации, полученной в результате решения производственной задачи (оптимизации процесса) в действие с последующим контролем эффективности результатов решения и, в случае необходимости, уточнение первоначальной цели.

---

<== предыдущая страница	|	следующая страница ==>
Выбор метода численного решения многокритериальных задач	|	Прогнозирование последствий от реализации принятых решений с использованием компьютерных моделей

---

Дата добавления: 2014-08-04; просмотров: 666; Нарушение авторских прав

---

Поделиться с ДРУЗЬЯМИ:

Мы поможем в написании ваших работ!