
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Выбор метода численного решения многокритериальных задач
На основании практического опыта решения оптимизационных задач можно заключить, что большинство из них многокритериальные. Также, справедливым можно считать утверждение о том, что для разработки алгоритма численного решения многокритериальных задач, последние, как правило, сводятся к однокритериальным. Действительно, одновременно достигнуть экстремальных значений нескольких критериев, особенно противоречащих друг другу, как правило, сложно, а в некоторых случаях невозможно. Следует отметить, что многокритериальные задачи по своей сути (формулировке, формализации и полученным с их помощью результатам) существенным образом отличаются от однокритериальных оптимизационных задач.
Проанализируем наиболее распространенные методы сведения многокритериальных задач к однокритериальным с целью выработки подходов для применения того, или иного метода для конкретных условий оптимизационных задач.
Предположим, что многокритериальная задача включает в себя m частных критериев оптимизации 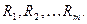
В качестве первого метода сведения многокритериальных задач к однокритериальным укажем подход, при котором в качестве обобщенного критерия используется функция 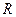 :
:
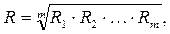
Существует целый класс задач оптимизации, для которых использование такого обобщенного критерия дает хороший практический результат.
В качестве второго метода представим подход, при котором в качестве обобщенного критерия выбирается критерий, представляющий частное двух величин:
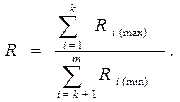
Использование на практике этого метода требует проведения дополнительных исследований с целью определения характерных зависимостей частных критериев от оптимизируемых переменных.
Следующий метод заключается в выборе в качестве обобщенного критерия взвешенную сумму частных критериев:
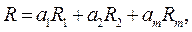
где 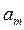 – весовые коэффициенты определяемые, иногда, субъективно.
– весовые коэффициенты определяемые, иногда, субъективно.
При этом некоторые коэффициенты 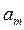 могут быть положительными, а некоторые отрицательными.
могут быть положительными, а некоторые отрицательными.
Одним из наиболее эффективных, по мнению автора, методов, применительно к решению производственных оптимизационных задач, является метод, когда из всех критериев 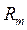 выделяют главный Ri, а все остальные Rj используются в виде ограничений. На практике верхняя и нижняя границы этих ограничений могут быть заданы сколь угодно близко, что позволит выбрать оптимизируемые переменные таким образом, что рассматриваемый критерий достигнет заданного значения с определенной степенью точности.
выделяют главный Ri, а все остальные Rj используются в виде ограничений. На практике верхняя и нижняя границы этих ограничений могут быть заданы сколь угодно близко, что позволит выбрать оптимизируемые переменные таким образом, что рассматриваемый критерий достигнет заданного значения с определенной степенью точности.
Следующий из рассмотренных в монографии методов заключается в присвоении каждому из частных критериев оптимизации некоторых значений и ранжировании критериев по этим значениям, либо в порядке возрастания, либо в порядке убывания. Поиск оптимального решения ведут последовательно. Изначально формируют все возможные решения. Затем выбирают из них все те, которые удовлетворяют первому критерию. Из сформированного подмножества решений выбирают те, которые удовлетворяют второму критерию и т. д. Этот метод легко реализуется численно. Вместе с тем, он не приемлем для решения задач, имеющих бесконечное число возможных решений. Кроме того, полученное с его помощью решение будет удовлетворять, лишь, измененным условиям задачи и поэтому не всегда будет оптимальным, т.е. наилучшим из всех возможных решений.
Метод последовательных уступок состоит в том, что изначально все частные критерии оптимизации R1, R2, … 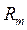 располагают в порядке убывания по их важности для решаемой практической проблемы. Выполнение этой процедуры, как правило, не вызывает сложностей у производственников. Затем определяют то решение, которое обеспечивает экстремум самому важному критерию. Исходя из практического опыта и интуитивного эвристического моделирования исследуемого процесса, решений, назначается некоторая уступка ΔR1, которая необходима для нахождения экстремума следующего по важности критерия R2. Затем назначается уступка ΔR2 и определяется решение обеспечивающее экстремум критерия R3 и т. д. Полученное таким образом решение, как и в предыдущем случае, будет являться квазиоптимальным, поскольку будет удовлетворять другим критериям Ri1 , где
располагают в порядке убывания по их важности для решаемой практической проблемы. Выполнение этой процедуры, как правило, не вызывает сложностей у производственников. Затем определяют то решение, которое обеспечивает экстремум самому важному критерию. Исходя из практического опыта и интуитивного эвристического моделирования исследуемого процесса, решений, назначается некоторая уступка ΔR1, которая необходима для нахождения экстремума следующего по важности критерия R2. Затем назначается уступка ΔR2 и определяется решение обеспечивающее экстремум критерия R3 и т. д. Полученное таким образом решение, как и в предыдущем случае, будет являться квазиоптимальным, поскольку будет удовлетворять другим критериям Ri1 , где
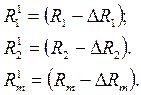
Значения ΔR1, ΔR2, … ΔRm выбирают исходя из конкретных обстоятельств и интуитивного моделирования исследуемого процесса. Этот метод является более предпочтительным для определенного класса оптимизационных задач по сравнению с методом ранжирования, поскольку содержит алгоритм определения изначальных значений частных критериев оптимизации.
§4.3 Использование подходов компьютерной математики в аналитико-экспериментальном методе формализации математических моделей принятия решений.
Для получения аналитических выражений функций, входящих в состав задачи (3.1), предполагается использовать их экспериментальные значения. Ниже приводятся результаты исследований, позволяющие получить аналитические выражения функций по их экспериментальным точкам с использованием специальных пакетов программ.
Как показано в [4], приближение функции аналитическим выражением, удовлетворяющим поставленным условиям, является распространенной задачей.
Для ее решения необходимо выбрать характерные точки функции и провести эксперимент при определенных значениях независимых переменных. Затем следует выбрать способ построения функции. Такими способами, в зависимости от содержания конкретной задачи, могут быть аппроксимация и интерполяция.
Аппроксимация – приближенное выражение математических величин (чисел, функций и др.) через другие, более простые, приближающие функции. Выбор приближающих функций является важным этапом. Приближающие функции могут быть выбраны в виде многочленов. В задачах приближения функций многочленами используется три класса функций: линейная комбинация степенных функций (ряд Тейлора, многочлены Лагранжа, Ньютона и др.); комбинация функций 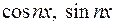 (ряды Фурье); комбинации функций exp(anx). При нахождении приближающей функции используют различные критерии согласия с экспериментальными данными, обеспечивающие выполнение требований заданной точности к аппроксимируемым функциям. На основе выбранных критериев согласия находятся параметры приближающих функций. В качестве критериев чаще всего выбирают минимум квадратов отклонений значений приближающей функции от эксперимента в узловых точках (метод наименьших квадратов) и минимум максимального отклонения (равномерное, чебышевское приближение). Также в качестве критерия может использоваться требование точного совпадения значений функций с экспериментом в узловых точках (параболическое приближение).
(ряды Фурье); комбинации функций exp(anx). При нахождении приближающей функции используют различные критерии согласия с экспериментальными данными, обеспечивающие выполнение требований заданной точности к аппроксимируемым функциям. На основе выбранных критериев согласия находятся параметры приближающих функций. В качестве критериев чаще всего выбирают минимум квадратов отклонений значений приближающей функции от эксперимента в узловых точках (метод наименьших квадратов) и минимум максимального отклонения (равномерное, чебышевское приближение). Также в качестве критерия может использоваться требование точного совпадения значений функций с экспериментом в узловых точках (параболическое приближение).
Известно, что аппроксимация непрерывной на отрезке 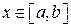 функции алгебраическими или тригонометрическими многочленами
функции алгебраическими или тригонометрическими многочленами 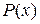 возможна с любой степенью точности (теорема Вейерштрасса). Мерой точности служит максимум разности между
возможна с любой степенью точности (теорема Вейерштрасса). Мерой точности служит максимум разности между 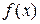 и
и 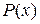 :
:
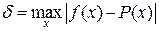
Аппроксимации (приближение) функций степенным рядом Тейлора, а также оценка погрешности формализуются в виде:
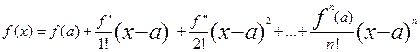 ,
,
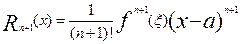 при
при 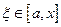
Расчет числовых коэффициентов степенного ряда, а также оценка погрешности могут быть получены с использованием специальных пакетов программ. Тем самым будет обеспечена аппроксимация функций степенным рядом Тейлора с использованием приемов компьютерной математики. Аналогичным образом решается вопрос и об аппроксимации функций рядом Фурье с использованием подходов компьютерной математики. Функция для такого случая записывается в виде:
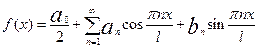 , где
, где 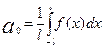 ,
, 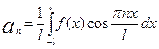 ,
,
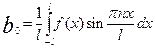 .
.
Аппроксимация функций рядом Фурье широко применяется при решении задач управления производством, в которых имеет место циклическое изменение во времени объемов производства или спроса на продукцию. Удобно с помощью рядов Фурье представление диаграмм работы машин периодического действия.
Применительно к задаче формализации математических моделей принятия решений с использованием аналитико-экспериментального подхода более приемлемым является метод интерполяции. Поскольку перед нами стоит задача построить приблизительно или точно аналитическое выражение функциональной зависимости, если о ней известно только соотношение между значением независимой переменной и соответствующими значениями функции в дискретном ряде точек. Основной задачей интерполяции, как раз, и является нахождение значения функции 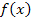 во всех точках заданных интервалом числовой оси. Другими словами интерполяция – это примерное вычисление функции
во всех точках заданных интервалом числовой оси. Другими словами интерполяция – это примерное вычисление функции 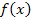 по нескольким значениям
по нескольким значениям 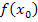 ,
, 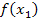 ,
, 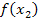 , …,
, …, 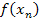 Є
Є 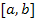 .
.
Интерполирование функции 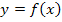 на отрезке
на отрезке 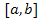 состоит в примерной замене функции
состоит в примерной замене функции 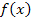 , заданной таблицей или графиком, ее аналитическим выражением. Точки
, заданной таблицей или графиком, ее аналитическим выражением. Точки 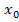 ,
, 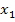 , …,
, …, 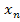 являются узлами интерполяции.
являются узлами интерполяции.
Важное значение имеет выбор шага между узлами интерполяции и выбор самих узловых точек, т.к. увеличение шага между узлами интерполяции может привести к большим погрешностям вычисления функции внутри интервала, а слишком выбранный малый шаг между узлами интерполяции приводит к значительному увеличению вычислений.
Наиболее простым методом интерполяции является метод линейной интерполяции. Рассмотрим этот метод подробнее с целью разработки алгоритмов использования специальных пакетов прикладных программ для представления функций в аналитическом виде по результатам эксперимента.
Под линейной интерполяцией понимаем интерполяцию значений функции в точках, полученных экспериментальным путем, линией 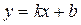 .
.
Суть задачи сводится к тому, что бы определить значение двух коэффициентов 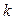 и
и 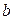 . Значение коэффициентов
. Значение коэффициентов  и
и 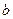 могут быть получены методом выбранных точек, либо путем минимизации алгебраических сумм отклонений экспериментальных точек от аппроксимирующей линии (метод средних) или минимизацией суммы квадратов отклонений экспериментальных точек от линии (метод наименьших квадратов).
могут быть получены методом выбранных точек, либо путем минимизации алгебраических сумм отклонений экспериментальных точек от аппроксимирующей линии (метод средних) или минимизацией суммы квадратов отклонений экспериментальных точек от линии (метод наименьших квадратов).
Метод выбранных точек заключается в том, что выбираются две точки 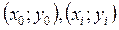 , отстоящие друг от друга по которым определяется линейная зависимость.
, отстоящие друг от друга по которым определяется линейная зависимость. 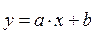 . Метод средних состоит в том, что коэффициенты
. Метод средних состоит в том, что коэффициенты  и
и 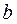 находятся из условия равенства нулю алгебраической суммы отклонений
находятся из условия равенства нулю алгебраической суммы отклонений  экспериментальных точек от прямой. Это условие математически записывается в виде:
экспериментальных точек от прямой. Это условие математически записывается в виде:
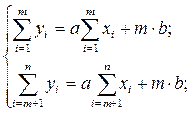
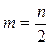 ;
;
Метод наименьших квадратов наиболее предпочтителен, так как требует равенства нулю суммы квадратов отклонений экспериментальных точек от экспериментальной кривой. Параметры  и
и 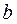 находятся из системы двух уравнений:
находятся из системы двух уравнений: 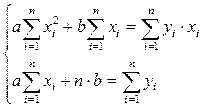
Достоинством метода линейной интерполяции является возможность его применения и в тех случаях, когда экспериментальные точки расположены на некоторых кривых, не являющихся графиками линейной функции. Это достигается за счет того, что во многих случаях не линейные зависимости могут быть приведены к линейному виду введением новых координат (переменных). Такая процедура носит название выравнивание зависимости. Выравнивание зависимостей можно осуществить логарифмированием, алгебраическими преобразованиями, заменой переменных. Если зависимость 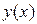 построить в новых координатах
построить в новых координатах 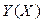 то она примет линейных вид.
то она примет линейных вид.
Например: Рассмотрим зависимость 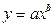 . Перейдем к новым координатам:
. Перейдем к новым координатам: 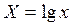 ,
, 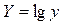 , тогда прологарифмировав начальное выражение, получим:
, тогда прологарифмировав начальное выражение, получим:
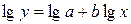
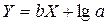
Из этого выражения могут быть найдены коэффициенты 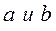 .
.
В [4] представлена таблица, содержащая виды функций и выравниваемые их переменные к линейному виду.
Таблица 5.1
| Формула | Выравниваемые переменные | Выровненная зависимость |
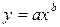
| 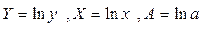
| 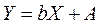
|
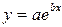
| 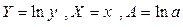
| 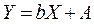
|
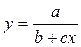
| 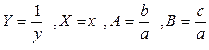
| 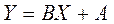
|
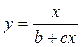
| 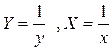
| 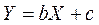
|
Достоинством применения простейших эмпирических формул (линейных или приводящихся к ним) является малое число коэффициентов, которые необходимо определять, возможность физической трактовки полученных формул при решении задачи оптимизации.
Для подбора вида эмпирических формул можно пользоваться атласом графиков, представленным в[4]. Иногда оказывается, что опытная кривая похожа на несколько кривых, уравнения которых различны. Чисто формальный выбор вида формулы может осуществиться с помощью следующей таблицы:
Таблица 5.2
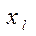
| 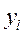
| формула |
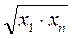
| 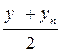
| 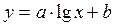
|
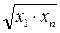
| 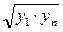
| 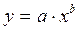
|
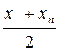
| 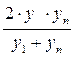
| 
|
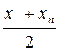
| 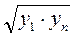
| 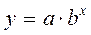
|
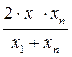
| 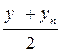
| 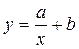
|
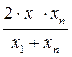
| 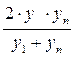
| 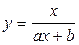
|
Из таблицы 5.2 опытных данных выбирают две точки 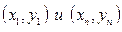 достаточно удаленных друг от друга и отстоящих от краев исследуемого интервала. Затем рассчитываются значения
достаточно удаленных друг от друга и отстоящих от краев исследуемого интервала. Затем рассчитываются значения 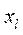 и
и 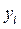 , и сравнивают для рассчитанного значения
, и сравнивают для рассчитанного значения 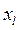 соответствующие ему значения
соответствующие ему значения 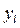 с экспериментальным значением
с экспериментальным значением 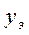 . В случае близкого совпадения
. В случае близкого совпадения 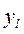 и
и 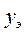 соответствующая формула считается подходящей, однако окончательное решение о том удачно ли описывает подобранная формула исследуемый процесс следует принимать после нахождения параметров
соответствующая формула считается подходящей, однако окончательное решение о том удачно ли описывает подобранная формула исследуемый процесс следует принимать после нахождения параметров  и
и 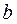 одним из трех вышеизложенных способов, а затем проверить которая формула более точно описывает исследуемый процесс путем расчета дисперсии отклонений. Та формула, для которой дисперсия отклонений меньше будет считаться лучше.
одним из трех вышеизложенных способов, а затем проверить которая формула более точно описывает исследуемый процесс путем расчета дисперсии отклонений. Та формула, для которой дисперсия отклонений меньше будет считаться лучше.
Использование представленных в данном параграфе таблиц совместно с пакетом программ Excel значительно расширяет возможности последнего, поскольку расширяет перечень видов функций, которые могут рассматриваться в качестве интерполирующих полученные экспериментальные данные.
Существуют и другие методы построения эмпирических формул. Один из них состоит в том, что в качестве функции, с помощью которой будет произведена интерполяция, выбирают алгебраический многочлен, принимающий в заданных точках установленное значение (интерполяционная формула Лагранжа). Интерполяционная формула Лагранжа используется, как правило тогда, когда нужно построить многочлен степени ''n'': 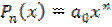 +
+ 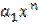 -1+…+
-1+…+ 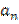 , который в точках
, который в точках 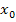 ,
, 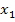 ,
, 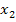 ,…,
,…, 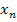 принимают заданные значения
принимают заданные значения 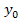 ,
, 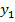 ,…,
,…, 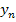 . Достоинством метода является то, что искомая функция проходит через все заданные точки, а недостатком - отсутствие достоверных значений функции между узловыми точками.
. Достоинством метода является то, что искомая функция проходит через все заданные точки, а недостатком - отсутствие достоверных значений функции между узловыми точками.
Из вышеизложенного можно заключить, что предложенный в главе 3 аналитико-экспериментальный метод формализации задач принятия решений может быть реализован на основе использования подходов компьютерной математики. Алгоритмы его использования могут быть, совершенно, различными, как и используемые при этом пакеты программ, в том числе и наиболее распространенный и доступный пакет – Excel. Общим остается изложенный в данном параграфе подход для решения таких задач.
Поскольку в рамках небольшого раздела монографии не представляется возможным исследовать все возможности использования подходов компьютерной математики для формализации задач принятия решений, поэтому ограничимся приведенным ниже примером представления функции в аналитическом виде по имеющимся значениям экспериментальных данных с использованием пакета Excel.
Пример алгоритма построения функции в аналитическом виде
с использованием подходов компьютерной математики.
1. Строим (вводим) в Excel таблицу исходных экспериментальных данных (например, в виде двух вертикальных колонок, слева - значения аргумента, справа - значения экспериментальные значения функции).
2. Вызываем процедуру " Мастер построения диаграмм" с помощью которой строим график искомой функции.
3. К линии построенного графика искомой зависимости "подводим" стрелочку и активизируем процедуру «Добавить линию тренда». Появляется возможность вызвать диалоговое окно, в котором можно подбирать различные виды математических зависимостей аппроксимирующие построенный график функции, оценивая каждую из них по значению критерия.
4. Уточняем (в случае необходимости) искомую функцию, используя для этой цели подход, определяемый таблицами 4.1, 4.2.
Определить зависимость y(x), в аналитическом виде можно более просто, если известны вид зависимости y от x и 2 точки, через которые проходит график функции.
Следует отметить, что с помощью описанного подхода может быть получен прогноз поведения во времени некоторых параметров, описывающих оптимизируемый процесс.
§4.4 Использование методов компьютерной математики для построения информационных и оптимизационных моделей производственных процессов
Рассмотрим некоторые конкретные примеры, по аналогии с которыми могут быть успешно использованы подходы компьютерной математики для численной реализации метода интеграционного моделирования. Приведенные ниже примеры информационных и оптимизационных моделей производственных процессов, также будут использованы для обоснованияалгоритма численной реализации интеграционных математических моделей.Под информационной математической моделью свойств исследуемого объекта, процесса, явления понимаем систему математических выражений (уравнений, неравенств), точно и однозначно описывающих исследуемые свойства объекта и дающая в процессе изучения объективную информацию о самом объекте.
Пример 1. Наглядный способ представления модели свойств объектов (моделируемых свойств объекта) может быть достигнут в виде ниже представленной таблицы Excel 5.3. Вертикальные колонки таблицы предназначены для хранения различных вариантов значений независимых и зависимых переменных. В первой вертикальной колонке могут быть указаны используемые в модели обозначения, а также представлен аналитический вид выражений, связывающих между собой зависимые переменные, независимые переменные и параметры модели. Горизонтальные строчки (с номерами 1 – 10 в таблице 5.3) предназначены для хранения значений переменных для различных вариантов численного эксперимента. Некоторые зависимые переменные (в примере это переменная обозначенная "У") могут быть заданы в качестве отдельных расчетных таблиц.

Параметры, которые для моделируемого процесса считаются постоянными, задаются, как правило, отдельной таблицей, заполнение которой относится к процессу "настройки" модели.
В качестве примера, поясняющего предложенный подход для построения информационных моделей, используемых в компьютерных моделях принятия решений, таблицами 5.3 – 5.4 представлена математическая модель проходки траншеи экскаватором. Геометрические размеры траншеи показаны на рис. 5.1.
Суть независимых и зависимых переменных, а также параметров модели , пояснена в таблицах 5.3 – 5.4. Введены следующие обозначения:
- П – производительность экскаватора в единицу времени;
- t – время работы (в относительных единицах),
- Ц – стоимость экскаватора;
- Но – норма амортизации.
В качестве моделируемых свойств производственного процесса выбраны зависимость пройденной длины траншеи от времени (l), количество руды добытое за интервал времени от t1 до t2 (Q), затраты на добытую руду (C).
С использованием представленной модели можно решать и самостоятельные производственные задачи (например, определить сколько понадобится времени на проходку траншеи длиной L м), а также получать графические зависимости независимых параметров от зависимых и находить их экстремальные значения.
Таблица 5.3
| Наименование модели | Независимые переменные | Моделируе- мые св-ва | |||||||||||
| Модель разработки траншеи экскаватором | № эксп | a | b | h | П | Ц | Но | Ки | У | t | l | Q | C |
Формулы
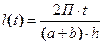 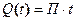
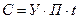 Обозначения
Обозначения
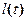 - длина траншеи; - длина траншеи;
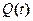 - количество породы; - количество породы;
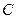 - себестоим. добытой породы; - себестоим. добытой породы;
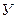 - себестоим. добычи м3 породы - себестоим. добычи м3 породы
| |||||||||||||
Таблица 5.4
| Наименование затрат | Значе – ние У. |
| Амортизация оборудования отнес к м3 добычи Ао | |
| Стоимость топлива на м3 добычи Ст | |
| Стоимость расходных материалов на м3 добыч Ср | |
| Стоимость добычи м3 породы (У) | У = Ао+ Ст + Ср |
Пример 2. Важным моментом построения информационных моделей является реализация алгоритмов численного решение уравнений, систем уравнений, дифференциальных уравнений, интегрирования и дифференцирования.Как уже указывалось, одним из универсальных способов построения таких алгоритмов является использование численных методов. Численные методы используются для приближения функций, для решения дифференциальных уравнений и их систем, для интегрирования и дифференцирования, для вычисления числовых выражений. Используемые при этом функции могут быть заданы аналитически, таблицей, графиком. В свою очередь, такие алгоритмы (построенные на основе численных методов) могут быть успешно реализованы с использованием специальных пакетов прикладных программ (таких, как Excel, Mat CAD). В ряде случаев можно обойтись без разработки специальных компьютерных программ.
Для численного решения уравнений может быть применен метод итераций или метод последовательных приближений. Метод итераций является одним из самых общих методов приближенного решения уравнений. Многие другие способы – частные случаи метода итераций. В основу приближенных вычислений и для оценки погрешностей используется понятие дифференциала.
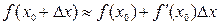 ,
, 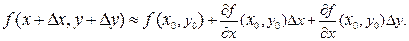
Алгоритм использования метода хорд для численного решения уравнений строится на следующей теореме. Если на отрезке 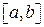 функция
функция 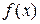 непрерывна, монотонна и принимает на концах отрезка значения различных знаков, то при правильном выборе одной из формул метод хорд дает последовательность точек, сходящихся к корню уравнения
непрерывна, монотонна и принимает на концах отрезка значения различных знаков, то при правильном выборе одной из формул метод хорд дает последовательность точек, сходящихся к корню уравнения 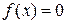 . Метод хорд заключается в последовательном приближении к значению x, являющемуся точным решением
. Метод хорд заключается в последовательном приближении к значению x, являющемуся точным решением 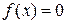 путем расчетов по формулам:
путем расчетов по формулам:
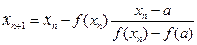 , или
, или 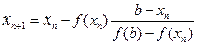
Другим частным случаем, метода итераций является метод Ньютона, который используется для приближенного решения алгебраических уравнений вида 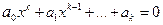 . Алгоритм последовательных приближений к точному решению формализуется в следующем виде:
. Алгоритм последовательных приближений к точному решению формализуется в следующем виде:
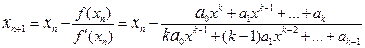 .
.
С помощью представленных выше алгоритмов могут быть решены многие уравнения. Существующие и доступные возможности компьютерной математики позволяют решить эти уравнения. В таком случае задача исследователя заключается в разработке алгоритма решения уравнения с помощью доступного пакета прикладных программ.
В качестве примера ниже приводится алгоритм решения уравнения с помощью программы Excel.
1. Вводим в произвольную ячейку значение нулевого приближения. Предположим, что эта ячейка имеет адрес А1.
2. В любую другую ячейку запишем выражение, представляющее собой левую часть уравнения. Пусть эта ячейка имеет адрес В1.
3. Нажимаем вкладку Сервис/Подбор параметра.
4. Во второй строчке активизированного диалогового окна устанавливаем значение равное правой части уравнения.
5. В третей строчке указываем адрес ячейки А1 и нажимаем клавишу "Ввод".
6. Результат решения задачи отразиться в ячейке А1, а погрешность подбора решения - в ячейке В1.
Численная реализация многих задач принятия решений, в том числе и оптимизационных задач построенных на основе вариационных методов, а также задач формализованных на основе методов математической физики, сводится, в конечном итоге, к решению систем линейных уравнений. В качестве примера, ниже приводится алгоритм решения системы линейных уравнений с программы Excel.
1.Вводим элементы основного определителя в ячейки электронных таблиц, предположим, что они заняли диапазон ячеек D1:D2.
2. Вводим столбец свободных членов. Предположим, что он занял диапазон ячеек D3:D4.
3. Рядом со столбцом свободных членов записываем столбец с названием неизвестных.
4. Объединяем ячейки для записи неизвестных.
5. Записываем, основную формулу МУМНОЖ(МОБР(D1:D2);D3:D4).
6.Одновременно нажимаем три клавиши, Ctrl+Shift+Enter, решение получено.
По мнению автора, разработка приемов использования численных методов совместно со специальными пакетами прикладных программ (такими, как Excel, Mat CAD) применительно к задачам принятия решений, является одним из способов развития компьютерной математики. С другой стороны, численные методы могут использоваться и, как самостоятельные методы, в том числе оптимизационные. Рассмотрим наиболее часто используемые алгоритмы численных методов, которые могут рассматриваться, как фрагменты, составляющие более сложные алгоритмы задач принятия решений, в том числе и решаемые с помощью методов компьютерной математики.
Пример 3. Численное дифференцирование используется чаще всего тогда, когда значения функции используются только в отдельных точках, например результаты эксперимента в виде таблиц. Тогда приближённое значение производной функции f(x) в точке x0 при выбранном шаге h находится на одной из формул:

Численное интегрирование осуществляется по алгоритму.
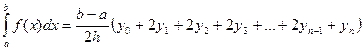
Наиболее важными являются численные методы решения дифференциальных уравнений. На практике, достаточно часто встречаются дифференциальные уравнения, решить которые в замкнутой форме не удаётся. В этом случае приходится применять приближённые методы. Одним из таких методов является метод, основанный на поиске решения в виде ряда Тейлора.
Рассмотрим алгоритм решения дифференциального уравнения 2-го порядка с использованием этого метода.
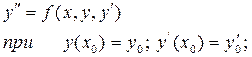
Решение ищем в виде
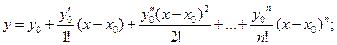
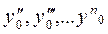 - находятся последовательным дифференцированием исходного уравнения
- находятся последовательным дифференцированием исходного уравнения 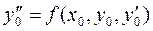 .
.
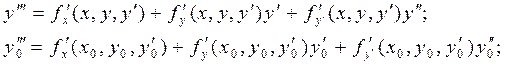
Определив коэффициенты ряда 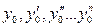 , останется исследовать только результат на сходимость решения.
, останется исследовать только результат на сходимость решения.
Для приближённого решения дифференциальных уравнений типа 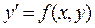 с начальными условиями
с начальными условиями 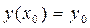 используется метод Пикара.
используется метод Пикара.
Решение уравнения ищется в виде ряда
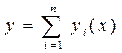 , где
, где 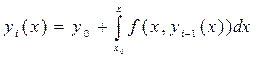 .
.
Для численного решения уравнений вида 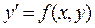 на отрезке
на отрезке 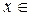 [a,b] , с заданной степенью точности
[a,b] , с заданной степенью точности 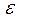 применяется метод Рунге-Кутта. Алгоритм решения уравнения начинается с выбора шага
применяется метод Рунге-Кутта. Алгоритм решения уравнения начинается с выбора шага 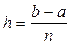 , причем так, чтобы
, причем так, чтобы 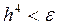 . Следующий этап алгоритма состоит в делении всей области поиска решения точками
. Следующий этап алгоритма состоит в делении всей области поиска решения точками 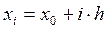 на отрезки.
на отрезки.
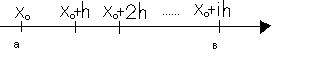
Затем определяют соответствующие значения 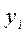 искомой функции, по формулам:
искомой функции, по формулам:
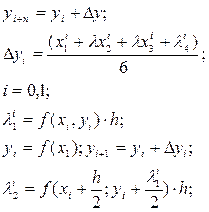
Этот метод также применяется для решения дифференциальных уравнений:
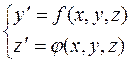
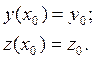
Методы компьютерной математики могут использоваться не только для построения информационных моделей производственных процессов, но и для численного решения оптимизационных задач принятия решений.
Пример 4. Ниже, представлен алгоритм численного решения задачи линейного программирования с использованием программы Excel.
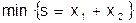 Необходимо найти при условии
Необходимо найти при условии
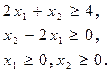 |
1. Озаглавим Х1,Х2, Х3 и т.д. ячейки в которых будут находиться неизвестные величины хi. В качестве таких ячеек выберем ячейки второй строки A2, B2, C2 и т. д.
2. Введем в ячейку A3 целевую функцию ( = A2 +B2).
3. Введем в ячейку A4 левую часть первого ограничения (= 2*A2 + B2): E
4. Введем в ячейку A5 левую часть второго ограничения (=B2 – 2*A2): E и т.д.
5. Введем в соответствующие ячейки остальные ограничения.
6. Переходим в меню поиска решения. Для этого активизируем команды Сервис: Поиск решения: Откроется диалоговое окно «Поиск решения».
7. Установим курсор в окошко «Установить целевую ячейку» и нажмем ЛК в поле ячейки, в которой записана целевая функция (в нашем примере это А3). Отметим точкой одну из процедур «Максимальное значение», «Минимальное значение».
8. Установим курсор в окошко «Изменяя ячейки» и протянем ЛК ячейки которые зарезервированы для хранения неизвестных (в нашем случае это ячейки А2, В2)
9. Нажмем ЛК клавишу «Добавить». Появится строчка диалогового меню для ввода ограничений. Курсор находится в окошке «Ссылка на ячейку». Нажать ЛК на ячейку в которой записана правая часть первого ограничения. В следующем окошке устанавливаем знак неравенства. В окошечко «ограничения» вводим числовое значение ограничения (в нашем случае это 4) Снова нажимаем клавишу «добавить» и вводим следующее ограничение и так до тех пор пока все ограничения, записанные в виде выражений в ячейках не будут введены.
10. Затем вводим ограничения выражающие условия, что искомые переменные больше нуля. При установленном курсоре в окошке «Ссылка на ячейку» нажимаем ЛК на ячейку отведенную для первой неизвестной (в нашем случае это А2). Выбираем знак больше – равно и в окошко «ограничения» устанавливаем «ноль». Эту процедуру повторяем для всех переменных.
11. Если в условии есть другие ограничения наложенные на переменные, (например Х1< 3), то эти ограничения вводятся аналогичным образом.
12. Если все ограничения введены, то нажимаем клавишу ОК и вновь выходим в диалоговое окно «Поиск решения». В нем отображены все введенные нами исходные данные. В окошке «ограничения» отображены все введенные нами ограничения. Любое из них можно выделить ЛК и изменить или удалить, нажав соответствующую клавишу. Нажав клавишу «Добавить» можно продолжить набор ограничений.
13. Нажимаем клавишу «Выполнить», появляется диалоговое окно «Результаты поиска решений». В ячейке предназначенной для целевой функции записано ее максимальное (минимальное) значение, а в ячейках для переменных записаны их значения, обеспечивающие экстремум функции, в ячейках для ограничений записаны значения ограничений при найденных значениях переменных.
По аналогии с представленным выше алгоритмом могут быть построены алгоритмы решения и других оптимизационных задач, использующие и другие пакеты специальных программ (например, Mat CAD).
переменных.
| <== предыдущая страница | | | следующая страница ==> |
| Сетевые методы. Методы теории графов | | | Глава 5 Использование теории вероятности и математической статики для построения математических моделей производственных процессов |
Дата добавления: 2014-08-04; просмотров: 736; Нарушение авторских прав

Мы поможем в написании ваших работ!