Прогнозирование последствий от реализации принятых решений с использованием компьютерных моделей

Согласно действующему законодательству, ответственность за последствия от практической реализации принятого решения несет лицо, принимающее данное решение. Поэтому, использование компьютерных моделей для принятия решений в производственных задачах не освобождает от ответственности соответствующих руководителей (лиц) за неправильно принятые решения. Следовательно важнейшей задачей при проектировании и эксплуатации КСПР является разработка мероприятий, направленных на обеспечение прогноза последствий от практической реализации принятого решения. Исследуем некоторые доступные для большинства предприятий

методы прогноза последствий от практической реализации принятых решений.

Прогнозирование применяется для определения основных направлений технического прогресса, развития отрасли, производственной мощности предприя­тий, возможных изменений техники, технологии и технико-экономи­ческих показателей предприятий в будущем.

Прогноз можно определить, как вероятностное суждение о состоянии какого-либо объекта (процесса или явления) в определенный момент времени в будущем и об альтернативных путях достижения каких-либо резуль­татов.

При прогнозировании, зачастую, имеет место неточное определение исходных данных, что особенно существенно сказывается при составлении прогнозов на большие сроки. В связи с этими обстоятельствами имеет место высокая степень неоп­ределенности прогнозной информации. Поэтому при составлении прогнозных моделей, чаще всего, используют стохастические или эвристические методы. Детерминированные методы для таких случаев применяются реже. Основными этапами прогнозирования являются ретроскопия, и проспекция. На стадии ретроскопии осуществля­ются сбор, хранение и обработка информации, оптимизация методов измерения и самой информации, на основе чего формируются струк­тура и состав характеристик объекта прогнозирования. На стадии диагноза осуществляется анализ объекта прогнозирования и состав­ляется прогнозная модель. При анализе сложного объекта исполь­зуются теории информации, измерений, распознавания образцов, которые помогают выбрать важнейшие, ведущие переменные (фак­торы) , минимизировать размерности описания, выбрать адекватные шкалы для измерения количественных и качественных показателей. Математические методы, применяемые в прогнозировании, основаны на теории вероятности и математической статистике, теории числен­ных методов, теории факторного анализа.

При разработке прогнозных моделей должны соблюдаться принципы системности анализа. В основе составления и анализа прогнозов лежат различные методы. Наиболее распространенными методами прогнозирования явля­ются экстраполяционные, статистические, экспертные. Экстраполяционные методы состоят в усреднении данных наблюдений в прошлом и настоящем и экстраполяция в будущее по­лученных зависимостей. Экстраполяция может осуществляться путем сглаживания и уравнивания статистическо­го ряда, описанием простыми зависимостями с использованием степенных полиномов, формализацией тенденций по огибающим кри­вым и др. Статистические методы используют корреляционный, регрессионный, факторный анализы. Экспертные и методы аналогий используют методы "Дельфи", эвристи­ческого прогнозирования, коллективной генерации идей (или "мозговой атаки") и др. В задачах прогнозирования используются такие математические методы, как математическое программирование, имитационное моде­лирование, методы статистических испытаний, теория игр, анализ случайных функций. Метод усреднения наблюдений основан на предположении о том, что судить о будущем можно по инфор­мации о прошлом и настоящем. Прогнозные значения параметров описывающих исследуемый процесс можно представить в виде сочетание двух со­ставляющих - детерминированной и случайной:

y(x)=f(x)+ŋ(x)

Считается, что f(х) представляет детерминирован­ную функцию от аргумента. Эта составляющая назы­вается трендом, тенденцией. Подбирается f (х) указанными выше способами, в том числе и в виде полинома. С повышением порядка последнего увели­чивается объем необходимой информации для его построения.

Составляющая ŋ (х) считается некоррелиро­ванной случайной функцией с нулевым математическим ожиданием. Роль ŋ (х) возрастает по мере увели­чения длительности прогноза или с ростом неопределенности системы. Оценка ŋ (х) в прогнозах — наибо­лее сложное дело. Здесь имеет место явление мас­штабного эффекта, под которым понимают погрешно­сти моделирования из-за нарушения подобия (струк­турного, геометрического, кинематического, термиче­ского и др.) модели и объекта прогнозирования. Ве­личина ŋ (х) характеризует нарушение подобия во взаимодействии тел с внешней средой. Оценка слу­чайности ŋ (х) проводится сравнением средних значе­ний параметров по критерию Стьюдента. Слагаемое ŋ (х) определяется вероятностной сущностью таких процессов, как, перенос вещест­ва, импульса, энергии. Оценка неслучайности ŋ (х) проводится сравнением дисперсий величин по крите­рию Фишера. Чем шире теоретическая информация о существе прогнозируемых процессов, тем с большим основани­ем можно экстраполировать эмпирическую формулу. Положительный результат достигается при сочетании, комбинировании различных методов прогнозирова­ния.

Прогнозируемые процессы и явления можно считать детерминированными,

для которых случайной составляющей можно с достаточной точностью пренебречь. Стохастическими считаются процессы и явления, в описании которых необходим учет случайной составляющей переменных в соответствии с требуемой точностью и задачей прогноза. К смешанным относят процессы и явления, имеющие детерминированные и стохастические ха­рактеристики.

В производственных задачах объекты прогнозирования являются в основном стохастическими и смешанными, некоторые из них с полным отсутствием ретроспективной информации (вновь проек­тируемые объекты).

По характеру развития объекты прогнозирования можно подраз­делить на дискретные, аперио­дические и циклические. У дискретных объектов прогнозирования тренд изменяется скачками в фиксированные моменты времени. У аперио­дических объектов тренд представляет собой апериодическую непрерыв­ной функции времени. Циклические объекты имеют регулярную состав­ляющую в виде периодической функции времени. При анализе дан­ных прошлого и выявления тенденций развития того или иного яв­ления важно учитывать возможные коренные изменения в технике и технологии в течение прогнозируемого периода.

Временные интервалы прогнозов могут изменяться в широких пределах — от часов до многих лет в зави­симости от содержания задачи. Они зависят от цик­личности воздействий в системе и должны быть дос­таточно велики, чтобы обеспечивалась возможность нашего влияния на ожидаемые изменения. Если про­цесс цикличен, то прогноз составляется на период не меньший, чем продолжительность цикла. Если прогнозируемый процесс имеет тенденцию к возрастанию в течение длительного времени, то прогноз должен рассчитываться на такой промежуток времени, за ко­торый можно осуществить мероприятия по сохране­нию экологического равновесия окружающей среды, наращиванию мощностей и приобретению необходи­мого для этих целей оборудования, внедрению рекомендаций по управлению процессом. Необходимость ставить на первое место сохране­ние равновесия в экосистеме обязывает менеджеров анализировать последствия производственных процессов на долговременный период. Задача очень сложная, связанная с применением решений в услови­ях риска и даже неопределенности из-за тесной вза­имной связи всех процессов в биосфере Земли.

Таким образом, прогнозирование решает следую­щие задачи: изучение тенденций изменения потребно­сти в тех или иных видах продукции и ресурсах; изучение спроса на производимые виды продукции, предсказание потребности в новых видах изделий в будущем; оценка и распределение сырьевых баз для различных направлений использования ресур­сов в народном хозяйстве; определение тенденций развития технологии и оборудования в различных отраслях; анализ воздействий производства на экосистему; выявление пер­спективных направлений развития отраслей; оценка обеспеченности всеми видами ресурсов, необ­ходимых для достижения поставленных целей; оты­скание оптимальных путей достижения производственных задач.

Основной задачей прогнозирования состояния объекта является разработка его адекватной модели, на основании ко­торой можно было бы судить о будущих состояниях объекта. Особенностью прогнозных моделей является то обстоятельство, что невозможно проведение прямой проверки соответствия модели и оригинала. В этом специфика и вместе с тем проблема моделирования будущего. Более распространены в прогнозных моделях графические изображения (так называемые "кривые роста") и математические описания. При отсутствии теоретических предпосы­лок о поведении объекта исследований в будущем, ис­пользуют методы аналогий и математической обра­ботки опытных данных, характеризующих прошлое и настоящее, подбора вида и параметров формул роста, на основании которых можно прогнозировать поведе­ние системы в будущем. Не следует забывать, что эм­пирическая формула справедлива лишь для интервала опытных значений, и экстраполяция связана с по­грешностью тем большей, чем дальше стремимся рас­пространить зависимость за пределы исследованного промежутка. С целью повышения достоверности про­гноза следует предусмотреть его определение несколькими различными методами. Это всегда дает хо­роший результат.

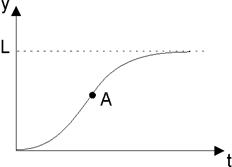Среди "кривых роста" в прогнозах особое место за­нимает S-образная кривая Перла (рис.7.1), которой "подчиняется" такие важные и сложные процессы, как из­менение эффективности тепловых электростанций, кпд паровых двигателей в течение всего периода их развития.

Как указано в [4], особенность кривой Перла состоит в ее построении на основе предположения о том, что скорость изменения функции пропорциональна ее текущему значению и расстоянию до асимптоты (возможного предела изменения функции). Кривая Перла позволяет предсказать скорость, с ко­торой новое технологическое решение вытесняет преды­дущее, устаревшее, используемое для получения той же продукции. В других случаях нас интересует скорость адаптации новой техники, так как естественно вначале недоверие к ней, внедрение новых идей идет трудно, и лишь постепенно темп растет. Со временем воз­можности существующей технологии исчерпываются, что характеризуется уменьшением скорости роста. На кривых Перла этот момент характеризуется точкой перегиба (точка А на рисунке). В подобных ситуациях возникает необходимость замещения старой техники, технологии новыми, основанными на революционных идеях и решениях. Многие исследователи считают, что замещение одной (старой) технологии другой (но­вой) представляется S-образными кривыми роста (Перла, Гомперца). Например, замена паруса двигателем, дерева — металлом в судостроении характеризу­ется S-образной кривой. Используя кривые роста, можно прогнозировать темпы увеличения характери­стик, определить "потолок", а при известном пределе можно предсказывать темп роста функциональных характеристик в будущий период. Одной из важней­ших проблем прогнозирования служит предсказание тенденций роста за пределами существующей техно­логии с учетом неизвестных в настоящее время новых видов продукции.

Следует отметить характерную ошибку в прогнозах, когда на основании постоянной скорости роста в прошлом предполагают ту же скорость процесса в бу­дущем. Такой подход в прогнозировании называется "наивным" в том смысле, что все происходящее в прошлом и сформировавшаяся тенденция в настоя­щем будут иметь место и в будущем. По крайней мере, в двух случаях "наивная экстраполяция" неприменима - при наличии естественного предела (истощение ресурса и др.) и при изменении факторов, обуславливающих тенден­цию в прошлом (темпы воздействие на ок­ружающую среду и др.). Достаточно часто в прогно­зах используют экспоненциальный рост, вызванный бурным развитием техники и технологии. Как указано в некоторых работах, экстрапо­ляция процесса в будущее в виде экспоненциальной функции в ряде случаев дает заведомо неверный ре­зультат.

Повысить достоверность модели прогноза можно, если учесть теоретические представления об изучае­мом процессе. Это позволяет ограничиться миниму­мом экспериментальных данных и дает возможность обоснованной экстраполяции за пределами проведен­ных исследований. В некоторых случаях удается вос­пользоваться известными заранее соотношениями для скорости протекания процессов, например, деформирования, нагревания, охлаждения, фильтрации и др.

Таким образом, степень достоверности прогнозной модели зависит от умения рассматривать си­туацию с различных точек зрения при сочетании раз­личных методов решения задачи.

В том случае, если прогнозная функция является функцией многих переменных, то она может быть представлена в виде композиции (в частном случае в виде произведения) нескольких функций от одной или нескольких переменных. Для этой цели может быть использован разработанный в главе 5 монографии аналитико- эксперементальный способ формализации функции многих переменных в виде композиции функций одной, двух, трех и т.д.

Дата добавления: 2014-08-04; просмотров: 513; Нарушение авторских прав

Мы поможем в написании ваших работ!