
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ММ-3. ПОНЯТИЯ, ИСПОЛЬЗУЕМЫЕ В ЧИСЛЕНЫХ МЕТОДАХ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ОБЫКНОВЕННЫХ И ЧАСТНЫХ ПРОИЗВОДНЫХ
Для изучения данной темы Вам необходимо восстановить в памяти:
- из элементарной геометрии - свойства треугольника;
- из курса прикладной математики - понятия линейной алгебры, векторной алгебры, числовой последовательности, функциональной последовательности, предела, определённого интеграла;
-из настоящего спецкурса - понятия: пространства, оператора, функционала.
2.2. Содержание темы
 2.2.1. Структурно – логическая схема содержания темы
2.2.1. Структурно – логическая схема содержания темы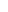
 2.2.2. Тематическое содержание
2.2.2. Тематическое содержание
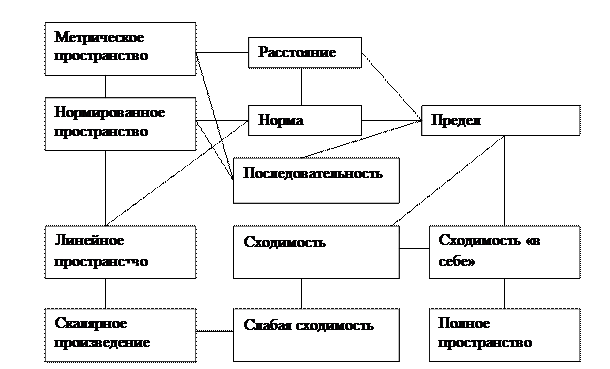
Перейдём непосредственно к величинам, которые могут характеризовать погрешность вычислений, если их результат имеет вид вектора или финкции (на самом деле такие характеристики погрешности могут быть применены для более широкого класса математических объектов, но для наших целей в этом нет необходимости). Одной из таких величин является расстояние между элементами (векторами или функциями) – очень далёкое обобщение понятия расстояния между точками в элементарной или аналитической геометрии. Обычно расстояние между элементами  ,
, 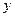 обозначается
обозначается  ,
,  или какой - либо другой буквой, но с расшифровкой обозначений.
или какой - либо другой буквой, но с расшифровкой обозначений.
Для использования этого понятия необходимо установить правило, по которому каждой паре элементов ставится в соответствие некоторое число; это число должно повторять основные свойства расстояния между точками. В то же время, оно должно характеризовать «близость» двух векторов или двух функций друг другу. Для одного и того же множества элементов можно вводить различные правила вычисления расстояния; эти правила должны соответствовать особенностям решаемой задачи.
Двум отмеченным выше  условиям новое понятие расстояния будет удовлетворять, если указанное правило обеспечивает выполнение трёх требований (они называются «аксиомами расстояния»):
условиям новое понятие расстояния будет удовлетворять, если указанное правило обеспечивает выполнение трёх требований (они называются «аксиомами расстояния»):
1) аксиома определённости -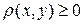 ,
,  (
( означает «тогда и только тогда»);
означает «тогда и только тогда»);
2) аксиома симметрии - 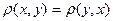 ;
;
3) аксиома треугольника 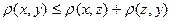 .
.
Аксиомы трегольника - обобщение свойств расстояния между точками пространства элементарной геометрии на новую область – множества произвольных элементов. Вводя конкретные правила, отвечающие приведенным выше аксиомам, мы вводим расстояние, иначе вводим метрику, или ещё иначе - метризуем пространство.

Мы занимаемся методами расчёта объектов из одной конкретной области, поэтому нас будут интересовать конкретные элементы вполне определённой природы, присущей этой области – вектора, функции, группы из нескольких пронумерованных функций одного и того же аргумента (одних и тех же аргументов), мыслимых как одно целое – вектор-функции. Для каждого множества можно предложить различные варианты метрик. Приведём примеры наиболее распространённых метрик (правил определения расстояния между элементами данного множества). Для каждого множества предложим два варианта, смысл и условия применения которых будут описаны позднее.
Расстояние между векторами. Пусть дано множество векторов 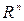 и два вектора
и два вектора  ,
, 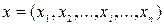 ,
, 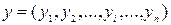 . Прямое обобщение расстояния аналитической геометрии даётся первым определением
. Прямое обобщение расстояния аналитической геометрии даётся первым определением
1в.  . (2.1)
. (2.1)
Иногда целесообразнее применять выражение
1в’.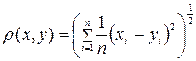 . (2.1’)
. (2.1’)
Одновременно в 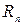 такая метрика гарантирует достаточную близость каждых
такая метрика гарантирует достаточную близость каждых 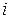 - ых компонент, если
- ых компонент, если 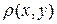 мало. Перед вычислениями, при анализе алгоритма, проще доказать возможность такого ограничения. Однако, в некоторых реальных ситуациях может быть важной возможность контроля близости каждой пары одноимённых компонент; например, в расчёте участвует вектор
мало. Перед вычислениями, при анализе алгоритма, проще доказать возможность такого ограничения. Однако, в некоторых реальных ситуациях может быть важной возможность контроля близости каждой пары одноимённых компонент; например, в расчёте участвует вектор  усилий в
усилий в 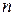 элементах конструкции с номерами
элементах конструкции с номерами 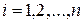 и нам необходимо обеспечить выполнение условия
и нам необходимо обеспечить выполнение условия 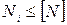 для каждого
для каждого 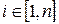 . В таких случаях принимается второе определение
. В таких случаях принимается второе определение
2в. . (2.2)
. (2.2)
Ограничение такого расстояния при вычислениях гораздо легче обеспечить.
Расстояние между функциями.На множестве функций могут быть введены метрики, аналогичные предложенным для 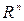 с теми же комментариями по поводу возможностей, которые предоставляет каждая из этих метрик.
с теми же комментариями по поводу возможностей, которые предоставляет каждая из этих метрик.
1ф. 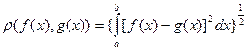 , (2.3)
, (2.3)
1ф’. , (2.3’)
, (2.3’)
2ф.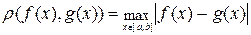 . (2.4)
. (2.4)
Естественно, интеграл в (1.3) должен существовать; можно доказать, что для этого должно выполняться требование 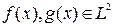 . Для того, чтобы условие (1.4) имело смысл в каждой точке
. Для того, чтобы условие (1.4) имело смысл в каждой точке 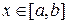 , нужно, чтобы выполнялось условие
, нужно, чтобы выполнялось условие 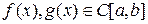 (в точках разрыва условие (1.4) теряет смысл).
(в точках разрыва условие (1.4) теряет смысл).
Расстояние (2.4) не меньше, чем (2.3’), поэтому соответствующий контроль погрешности или сходимости более «жёсток».
Расстояние между вектор-функциямиможно получить комбинированием введенных выше определений.
Пример 1.

Пример 2.
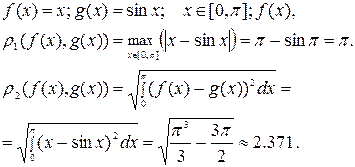
|
 Таким образом, пространства
Таким образом, пространства 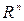 ,
,  ,
,  можно превратить в метрические пространства, введя в них метрику.
можно превратить в метрические пространства, введя в них метрику.
Следует особо подчеркнуть, что два одинаковых множества с различными метриками являются различными метрическими пространствами.
Практически для всех объектов, с которыми нам придётся иметь дело (вектора, функции, вектор-функции), определены операции сложения и умножения на число, обладающие обычными, известными из элементарной математики свойствами. Множества таких элементов (любого из этих типов) называются линейными системами, или линейными пространствами, если они удовлетворяют следующим условиям:
1) если элементы 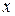 ,
,
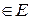 (
(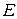 - линейное пространство), а
- линейное пространство), а  и
и 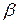 - числа (более общие случаи мы не рассматриваем), то элемент
- числа (более общие случаи мы не рассматриваем), то элемент 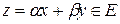 ;
;
2) существует нулевой элемент 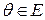 такой, что для всякого
такой, что для всякого 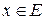 (будем обозначать это так:
(будем обозначать это так: 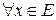 ) справедливо
) справедливо  .
.
|
.
.
Если множество объектов, используемых в расчёте, является линейным пространством, можно ввести более удобную меру погрешности – норму разности точного и приближённого решения. Дело в том, что в линейном пространстве определена разность элементов пространства (в метрическом пространстве операции сложения или вычитания и умножения на число не определены), а при умножении элемента на число известно, что произойдёт с его нормой. Норма служит количественной характеристикой одного элемента (именно разности точного и приближённого решений), а не двух, как расстояние. Норма является обобщением понятия длины вектора; она обладает многими её свойствами.
Это обеспечивается правилами определения нормы, которые удовлетворяют специальным требованиям (аксиомам нормы).
|
1) аксиома определённости 

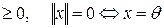 ;
;
2) аксиома однородности – если  -число,то
-число,то 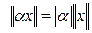 ;
;
3) аксиома треугольника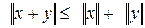 .
.
Введём в нормированном пространстве метрику по правилу
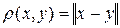 . (2.5)
. (2.5)
Можно доказать, что такое правило удовлетворяет всем аксиомам расстояния. Следовательно, можно утверждать, что нормированное пространство всегда можно считать метрическим пространством. При этом норма элемента будет равна
 - (2.6)
- (2.6)
его расстоянию от нулевого элемента. Обратное не  всегда верно, так как не любое метрическое пространство может обеспечить удовлетворение требования однородности. Однако, рассматриваемые нами пространства все нормированные и, следовательно, все метрические.
всегда верно, так как не любое метрическое пространство может обеспечить удовлетворение требования однородности. Однако, рассматриваемые нами пространства все нормированные и, следовательно, все метрические.
Дадим примеры норм для объектов, для которых мы вводили метрику.
Норма вектора.Пусть имеется вектор 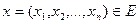 ,
,  - линейное пространство. Опираясь на соответствие между расстоянием и нормой, устанавливаемое формулой (1.6), введём нормы по формулам, равносильным расстояниям по формулам (1.1) и(1.2). Если нас интересует только среднеквадратичная величина компонент, можно пользоваться определением 1в
- линейное пространство. Опираясь на соответствие между расстоянием и нормой, устанавливаемое формулой (1.6), введём нормы по формулам, равносильным расстояниям по формулам (1.1) и(1.2). Если нас интересует только среднеквадратичная величина компонент, можно пользоваться определением 1в
1в. 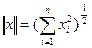 . (2.7)
. (2.7)
Это обобщение понятия «длина вектора» из векторной алгебры. Второе определение, равносильное расстоянию (1.2), применяется в случае, когда нас интересует максимальная по модулю компонента (случай 2в)
2в. 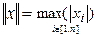 . (2.8)
. (2.8)
Пример 3.
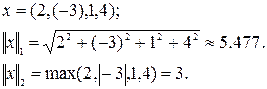
Норма функции.По аналогии с определениями расстояния между функциями дадим определения нормы функции.
Для функций  , если достаточно оценить «среднеквадратичное» значение функции, можно воспользоваться определением (1.3) и ввести норму
, если достаточно оценить «среднеквадратичное» значение функции, можно воспользоваться определением (1.3) и ввести норму
1ф.  . (2.9)
. (2.9)
В случае, если функция  и нам необходимо оценить наибольшее по модулю значение функции на этом отрезке, можно воспользоваться вторым определением расстояния между функциями и формулой (1.6)
и нам необходимо оценить наибольшее по модулю значение функции на этом отрезке, можно воспользоваться вторым определением расстояния между функциями и формулой (1.6)
2ф. 
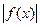 . (2.10)
. (2.10)
Принятие правила определения нормы для данного пространства называется введением в него нормы.
Пример 3.
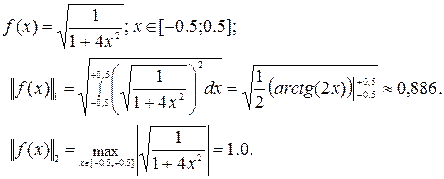
|
При выполнении приближённых расчётов обычно требуется получить не одно, а несколько следующих друг за другом решений, причём есть основание предполагать, что каждое следующее решение точнее предыдущего (в заранее обусловленном смысле). Сравнение оценки погрешности каждого полученного решения с некоторой допускаемой величиной позволяет обоснованно остановиться на одном из них и считать его окончательным результатом расчёта. Таким образом возникает необходимость во введении понятия последовательности элементов и изучении её свойств, во многом аналогичных свойствам знакомой нам из курса прикладной математики числовой последовательности.

Последовательность элементов  метрического пространства
метрического пространства  обозначается
обозначается  или
или  .
.
По аналогии с числовой последовательностью для последовательности элементов метрического (а, значит, и нормированного, как частный случай) пространства можно ввести понятия сходимости и предела. Для этого используется известное понятие – предела числовой последовательности, а именно – последовательности расстояний в метрическом пространстве и нормы – в нормированном пространстве.
Для последовательности элементов 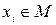 метрического пространства
метрического пространства 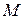 понятие предела определяется следующим образом.
понятие предела определяется следующим образом.
|
Аналогично этому определяется предел последовательности элемнтов 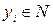 нормированного пространства
нормированного пространства  .
.
|
В обоих указанных пространствах справедливо следующее утверждение: если последовательность имеет предел, то он всегда единственный.
Сходимость последовательности в метрическом пространстве называется сходимостью по расстоянию, а её сходимость в нормированном пространстве – сходимостью по норме.
В метрическом пространстве различают:
-сходимость «в среднем» - при определении расстояния между векторами по формуле (1.1) и между функциями – по формуле (1.3);
-покоординатную сходимость – при определении расстояния между векторами по формуле (1.2).
-равномерную сходимость – при определении расстояния между функциями по формуле (1.4).
Аналогично этому в нормированном пространстве, с учётом того, что оно является частным случаем метрического пространства и постулируется (1.5), различают:
-сходимость «в среднем» - при определении нормы разности векторов по формуле (1.7) и нормы разности функций – по формуле (1.9);
-покоординатную сходимость – при определении нормы разности векторов по формуле (1.8);
-равномерную сходимость – при определении нормы разности функций по формуле (1.4).
В пространстве 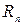 сходимость в среднем и сходимость по координатам эквивалентны. В пространстве
сходимость в среднем и сходимость по координатам эквивалентны. В пространстве  в общем случае это неверно. Рассмотрим эту ситуацию подробнее. Выделим в этом пространстве функции, интегрируемые с квадратом., то – есть, одновременно принадлежащие пространству
в общем случае это неверно. Рассмотрим эту ситуацию подробнее. Выделим в этом пространстве функции, интегрируемые с квадратом., то – есть, одновременно принадлежащие пространству  . Множество таких функций обозначается
. Множество таких функций обозначается  . На этом множестве равномерная сходимость влечёт за собой сходимость в среднем, но не наоборот: при наличии сходимости в среднем отклонения функций в некоторых точках может быть недопустимо большим. В таких случаях необходимо требовать обеспечение равномерной сходимости.
. На этом множестве равномерная сходимость влечёт за собой сходимость в среднем, но не наоборот: при наличии сходимости в среднем отклонения функций в некоторых точках может быть недопустимо большим. В таких случаях необходимо требовать обеспечение равномерной сходимости.
Естественно, далеко не любая последовательность имеет предел. В то же время, для разработки или применения метода, приводящего к последовательности приближённых решений, необходимо доказать два утверждения: во-первых, необходимо доказать, что эта последовательность сходится; во-вторых, что её предел равен точному решению (хотя, как указывалось выше, точное решение не известно и именно поэтому разыскивается приближённое).
Определение предела последовательности или даже установление факта наличия такого предела является достаточно сложной задачей. В связи с этим полезно ввести некоторые новые понятия.

Элементы фундаментальной последовательности как бы сближаются друг с другом при одновременном увеличении их номеров.
Сходимость в себе гораздо легче контролировать в процессе расчёта – ведь приближённые решения с разными номерами известны, они определяются в результате расчёта. Кроме того, в процессе теоретического анализа схемы приближённого расчёта также установление факта сходимости в себе в ряде случаев проще. Поэтому важное значений имеет установление условий, при которых наличие сходимости в себе гарантирует наличие сходимости в смысле определений 2.7 и 2.8. Эти условия выполняются в так называемых полных пространствах.Если мы выбираем решение из полного пространства, то достаточно показать, что последовательность приближённых решений фундаментальна.

Полными могут быть: метрические пространства и нормированные пространства (как частный случай метрических).
 Полное нормированное пространство называется банаховым пространством (по имени выдающегося польского математика С. Банаха, построившего основы теории нормированых пространств).
Полное нормированное пространство называется банаховым пространством (по имени выдающегося польского математика С. Банаха, построившего основы теории нормированых пространств).
Прстранства  - полные пространства, то – есть, в них любые фундаментальные последовательности имеют предел (и он принадлежит тому же пространтсву). Здесь имеется ввиду, что в пространстве
- полные пространства, то – есть, в них любые фундаментальные последовательности имеют предел (и он принадлежит тому же пространтсву). Здесь имеется ввиду, что в пространстве  должна обеспечиваться равномерная сходимость.
должна обеспечиваться равномерная сходимость.
Большое значение в прикладном анализе имеют также пространства, у которых пределы всех сходящихся последовательностей принадлежат этому же пространству.
.
|

Замыкание множества 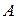 обозначается
обозначается 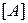 (иногда
(иногда  ).
).
В векторной алгебре чрезвычайно важна роль понятия «скалярное произведение». При помощи скалярного произведения определяются длина вектора, его проекция на заданное направление, угол между векторами; в механике при его помощи определяется работа силы. В лекции ММ-1 отмечалось, что функциональный анализ является далеко идущим обобщением несокльких математических дисциплин, в том числ – векторной алгебры. В большой степени это относится и к вводимому в функциональном анализе понятию скалярного произведения.
|
Если в линейном пространстве задано указанное соответствие (задан способ определения скалярного произведения), то говорят, что в нём задано скалярное произведение.
|
Евклидово пространство иногда называют унитарным (обычно, если числа в определениях линейного пространства и скалярного произведения комплексные).
Полное евклидово пространство называется гильбертовым пространством по имени выдающегося немецкого математика Д. Гильберта, много занимавшегося основополагающими математическими проблемами.
Укажем возможные способы определения скалярного произведения.
Скалярное произведение векторов. Для определения скалярного произведения векторов из 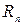 принимается выражение, являющееся прямым обобщением скалярного произведения векторной алгебры. Пусть
принимается выражение, являющееся прямым обобщением скалярного произведения векторной алгебры. Пусть 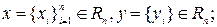 тогда
тогда
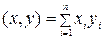 . (2.11)
. (2.11)
Скалярное произведение функций. Для этой цели используется обобщение выражения (2.11) на случай функции - «вектора с континуальным множеством компонент» (компонентами этого вектора являются значения функции при различных значениях аргумента). Пусть 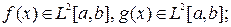 тогда
тогда
 . (2.12)
. (2.12)
Соответствие таких выражений требованиям к скалярным произведениям доказана. Эти доказательства приведены в курсах функционального анализа. Там же доказывается законность введения нормы вектора или функции по формуле

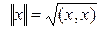 . (2.13)
. (2.13)
Это норма, порождённая скалярным произведением.
Таким образом, любое евклидово пространство превращается в нормированное.
|
Иногда для построения приближённого метода оказывается удобным применять понятие слабой сходимости. Оно также отталкивается от понятия числовой последовательности (последовательности скалярных произведений).
|
 .
.
2.3. Критерии усвоения
После изучения содержания данной темы Вы должны:
·
| |
для чего применяются понятия «расстояние» и «норма» в прикладном анализе;
что такое «предел последовательности»;
что такое «сходимость в среднем» и «равномерная сходимость» и когда применяется каждое из них;
что такое «фундаментальная последовательность»;
какое пространство называется полным;
какое множество называется замкнутым;
как определяется скалярное произведение;
· понимать
смысл понятий «расстояние» и «норма»;
почему норма задаётся только в линейном пространстве;
смысл понятия «предел последовательности»;
почему в различных ситуациях необходимо контролировать либо сходимость в среднем, либо сходимость равномерную;
почему нормированное пространство одновременно является метрическим, а евклидово – нормированным.
· Уметь
Находить расстояния различных типов между векторами и функциями.
2.4. Выход темы в другие темы и дисциплины
Данная тема имеет выход в дипломные, магистерские и диссертационные работы.
2.5. Тест - контроль для самопроверки
2.1. Что такое расстояние между элементами пространства?
А. Число, задаваемое формулой (2.1).
Б. Число, задаваемое формулой (2.4).
В. Число, задаваемое формулой (2.6).
Г. Число, правило определения которого обеспечивает выполнение аксиом расстояния
2.2. Что такое метрическое пространство?
А. Множество,на котором введена метрика.
Б. Пространство, на котором расстояние определяется по формуле (2.4).
В. Пространство, на котором определены сложение и умножение на число.
Г. Полное метрическое пространство.
2.3. По какой формуле определяется расстояние между векторами при контроле покоординатной сходимости?
А. 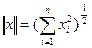 .
.
Б.  .
.
В. 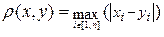 .
.
Г.  .
.
2.4. По какой формуле определяется расстояние между векторами при контроле сходимости в среднем?
А. 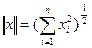 .
.
Б.  .
.
В. 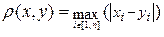 .
.
Г. 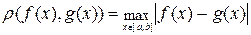 .
.
2.5. . По какой формуле определяется расстояние между функциями при контроле сходимости в среднем?
А. 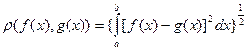 ,
,
Б. 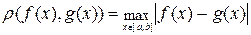 .
.
В.  .
.
Г.  .
.
2.6. . По какой формуле определяется расстояние между функциями при контроле равномерной сходимости?
А. 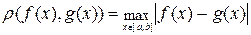 .
.
Б. 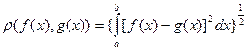
В. 
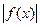 .
.
Г.  .
.
2.7. Что называется полным пространством?
А. Пространство, в котором каждая фундаментальная последовательность имеет предел.
Б. Пространство, в котором задана норма.
В.Пространство, которому принадлежат пределы всех сходящихся последовательностей его элементов.
Г. Пространство, на котором задано скалярное произведение.
2.8. Что называется скалярным произведением элементов пространства?
А. Норма их разности.
Б. Расстояние между ними.
В. Число, правила определения которого обеспечивают выполнение следующих требований:
а) симметрии (коммутативности) 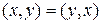 ;
;
б) дистрибутивности 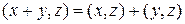 ;
;
в) однородности  , где
, где  - действительное число;
- действительное число;
г) определённости 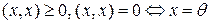 .
.
Г. Произведение их пределов.
2.9. Что называется банаховым пространством?
А. Полное метрическое пространство.
Б. Полное евклидово пространство.
В. Полное нормированное пространство.
Г. Пространство, на котором задано скалярное произведение.
2.10. Что называется гильбертовым пространством?
А. Полное метрическое пространство.
Б. Полное евклидово пространство.
В. Полное нормированное пространство.
Г. Пространство, на котором задано скалярное произведение.
Ответы на тест-самоконтроль 2.5 (адрес файла Блок 3 -----)
2.1. «Г» - число, правила определения которого обеспечивают выполнение аксиом расстояния.
2.2. «А» - Множество, на котором введена метрика.
2.3. «В» - 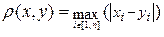 .
.
2.4. «Б» -  .
.
2.5. «А» - 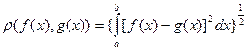 .
.
2.6. «А» - 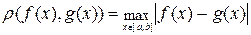 .
.
2.7. «А» - Пространство, в котором каждая фундаментальная последовательность имеет предел.
2.8. «В» - Число, правила определения которог обеспечивают выполнение требований:
симметрии (коммутативности) 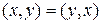 ;
;
дистрибутивности 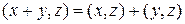 ;
;
однородности  ;
;
определённости 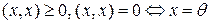 .
.
2.9. «В» - Полное нормированное пространство.
2.10. «Б» - Полное евклидово пространство.
.
 | |||||
 | |||||
 | |||||
 |
ММ-3. ПОНЯТИЯ, ИСПОЛЬЗУЕМЫЕ В ЧИСЛЕНЫХ МЕТОДАХ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ОБЫКНОВЕННЫХ И ЧАСТНЫХ ПРОИЗВОДНЫХ
ММ-3. Ключевые слова и понятия
3.1. Системы элементов
3.2. Линейная комбинация элементов данной системы.
3.3. Линейная оболочка системы элементов.
3.4. Линейная независимость элементов конечной системы
3.5. Линейная независимость элементов бесконечной системы
3.6. Линейная зависимость элементов
3.7. Подпространство 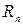 .
.
3.8 Подпространство метрического пространства.
3.9. Подпространство линейного пространства.
3.10. Подпространство полного линейного метрического пространства
3.11. Подпространство нормированного пространства
3.12. Размерность
3.13. Базис.конечномерного пространства.
3.14. Базис.бесконечномерного пространства.
3.15. Ортогональная система элементов.
3.16. Ортогональная система элементов, полная в евклидовом пространстве
3.17. Проектирование в подпространство.
3.18. Энергетическое произведение.
3.19. Энергетическая норма.
3.20. Энергетическое пространство оператора.
| <== предыдущая страница | | | следующая страница ==> |
| Входная информация для самопроверки. Для изучения данной темы Вам необходимо восстановить в памяти | | | Входная информация для самопроверки. Для изучения данной темы Вам необходимо восстановить в памяти |
Дата добавления: 2014-04-15; просмотров: 534; Нарушение авторских прав

Мы поможем в написании ваших работ!
 , а
, а  .
Вернитесь к тексту
.
Вернитесь к тексту
 .
Норма элемента
.
Норма элемента  метрического пространства
метрического пространства  , если
, если 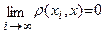 .
Вернитесь к тексту
.
Вернитесь к тексту
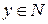 нормированного пространства
нормированного пространства  , если
, если  Вернитесь к тексту.
Вернитесь к тексту.
 - линейное пространство; если любым двум элементам
- линейное пространство; если любым двум элементам 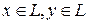 поставлено в соответствие число, в нашем курсе – действительное, обозначаемое как
поставлено в соответствие число, в нашем курсе – действительное, обозначаемое как 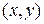 , и это соответствие удовлетворяет следующим условиям
а) симметрии (коммутативности):
, и это соответствие удовлетворяет следующим условиям
а) симметрии (коммутативности): 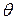 - нулевой элемент данного линейного пространства,
- нулевой элемент данного линейного пространства, 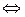 обозначает «тогда и только тогда»),
то это число называется скалярным произведением элементов
обозначает «тогда и только тогда»),
то это число называется скалярным произведением элементов  ┴
┴ , если
, если 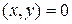 .
Вернитесь к тексту
.
Вернитесь к тексту
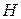 и его элементы
и его элементы 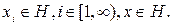 Последовательность
Последовательность 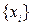 называется слабо сходящейся к
называется слабо сходящейся к 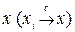 , если
, если 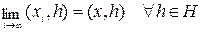 .
Вернитесь к тексту
.
Вернитесь к тексту