
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Входная информация для самопроверки. Для изучения данной темы Вам необходимо восстановить в памяти
Для изучения данной темы Вам необходимо восстановить в памяти:
-из курса прикладной математики – разложение вектора по ортам; проектирование вектора на плоскость и ось; скалярное произведение векторов в векторной и линейной алгебре; определённый интеграл;
-из настоящего спецкурса - понятия: пространства, оператора, последовательности, функциональной последовательности, предела, сходимости.
2.2. Содержание темы

2.2.1.Структурно-логическая схема содержания темы 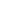
 2.2.2. Тематическое содержание
2.2.2. Тематическое содержание
При разработке численных методов возникает необходимость выразить какой-либо элемент некотрого пространства, искомый или заданный, через некоторые заранее выбранные элементы того же пространства. Для последующего использования эти элементы следует упорядочить, например, пронумеровать. В качестве примера можно привести разложение вектора на компоненты 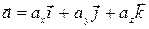 (вектор
(вектор 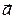 выражен через заранее выбранные элементы, расположенные в определённом порядке – орты
выражен через заранее выбранные элементы, расположенные в определённом порядке – орты 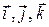 ). Эти орты иногда обозначают как нумерованные элементы
). Эти орты иногда обозначают как нумерованные элементы 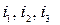 или
или 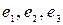 . Другим примером может служить разложение функции в функциональный ряд. В этой связи можно упомянуть: степенной ряд
. Другим примером может служить разложение функции в функциональный ряд. В этой связи можно упомянуть: степенной ряд 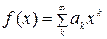 , где функцция
, где функцция 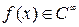 выражена через заранее выбранные элементы – функции
выражена через заранее выбранные элементы – функции 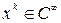 ; тригонометрический ряд
; тригонометрический ряд 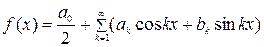 , где функция
, где функция 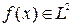 выражена через заранее выбраные элементы – функции 1,
выражена через заранее выбраные элементы – функции 1, 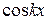 ,
, 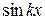 , также принадлежащие
, также принадлежащие  . Упорядоченная совокупность таких заранее выбранных элементов некоторого пространства называют системой элементов этого пространства.
. Упорядоченная совокупность таких заранее выбранных элементов некоторого пространства называют системой элементов этого пространства.
|
Систему элементов  иногда обозначают
иногда обозначают 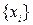 .
.
Такую приближённую замену одного элемента другим называют аппроксимацией.
Здесь мы будем рассматриватьтолько один вариант аппроксимации – линейную аппроксимацию, или аппроксимацию при помощи линейной комбинации заданных элементов линейного пространства (так как такая аппроксимация предусматривает умножение элементов на число и их сложение).

При изменении чисел 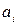 изменяется линейная комбинация. Перебирая всевозможные сочетания этих чисел, мы получим множество линейных комбинаций элементов
изменяется линейная комбинация. Перебирая всевозможные сочетания этих чисел, мы получим множество линейных комбинаций элементов  . Так можно прийти к понятию множества всех линейных комбинаций этих элементов (их бесконечно много).
. Так можно прийти к понятию множества всех линейных комбинаций этих элементов (их бесконечно много).

Говорят, что линейная оболочка порождена элементами  .
.
Линейная оболочка является также линейным пространством, так как каждая линейная комбинация вместе с порождающими оболочку элементами принадлежит ей.

Возможны случаи, когда требуется установить, является ли линейно независимой бесконечная система элементов.(например, в пространстве  ).
).


Обычно приближённое решение выбирается не из всех элементов пространства, а из некоторого их подмножества. Это подмножество должно быть пространством, одноимённым данному (метрическим, линейным, нормированным, и т.д.). В наиболее важных случаях, когда процесс решения должен порождать последовательности приближённых решений, оно должно содержать в себе пределы всех сходящихся последовательностей своих элементов. Эти подмножества называются подпространствами.
|


|

|
.
.
.
|
Нулевой элемент линейного протранства и само линейное пространство являются подпространствами этого пространства.
Примеры подпространств. В трёхмерном пространстве элементарной геометрии, рассматриваемом как линейное пространство радиусов-векторов его точек, подпространствами являются трёхмерная область, плоскость, прямая; в метрическом пространстве, образованном функциями класса 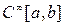 и метрикой
и метрикой 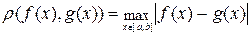 , подпространством является множество многочленов заданной степени; в нормированном пространстве подпространством является класс
, подпространством является множество многочленов заданной степени; в нормированном пространстве подпространством является класс  (можно доказать, что он является замкнутым множеством).
(можно доказать, что он является замкнутым множеством).
Все рассматривавшиеся линейные пространства, а также их подпространства 3.6, 3.7, 3.8 порождаются системами своих элементов.
|

Так, известное из линейной алгебры пространство 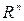 векторов
векторов 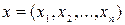 имеет конечную размерность
имеет конечную размерность 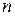 . Пространство
. Пространство  бесконечномерно.
бесконечномерно.
Для того, чтобы можно было выразить каждый элемент какого-либо линейного пространства в виде линейной комбинации элементов какой-то системы элементов этого пространства, нужно подчинить выбор этой системы элементов определённым условиям. Система элементов, удовлетворяющая таким условиям, называется базисом этого пространства. У каждого пространства таких базисов может быть бесконечно много. Каждое подпространство пространства, имеющего базис, ведёт себя, как всё пространство, в котором оно содержится, поэтому также имеет базис.

Примеры базисов конечномерных пространств.Базисом трёхмерного пространства элементарной геометрии может быть система его ортов 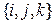 . Для множества
. Для множества 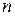 -мерных векторов линейной алгебры базисом может служить система единичных векторов
-мерных векторов линейной алгебры базисом может служить система единичных векторов 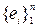 , где
, где 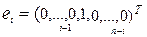 , то-есть, это вектор, единственный ненулевой элемент которого (единичный) стоит на
, то-есть, это вектор, единственный ненулевой элемент которого (единичный) стоит на  -ом месте.
-ом месте.
Любой элемент конечномерного пространства может быть разложен в линейную комбинацию элементов базиса.
Бесконечномерное пространство в общем случае может не иметь базиса. Если он всё же существует, он обязательно бесконечен. Для нас интересен случай, когда он счётен. Пространство  имеет счётный базис (на самом деле – бесконечно много счётных базисов). Определения счётного базиса практически бесполезны для приложений, так как неконструктивны (не дают непосредственно пути построения такого базиса). Ими также трудно воспользоваться для отбраковки систем, не являющихся базисом.
имеет счётный базис (на самом деле – бесконечно много счётных базисов). Определения счётного базиса практически бесполезны для приложений, так как неконструктивны (не дают непосредственно пути построения такого базиса). Ими также трудно воспользоваться для отбраковки систем, не являющихся базисом.
|
В этом смысле базис – полная система элементов любого нормированного пространства, в том числе – пространств 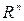 и
и  . Система элементов нормированного пространства полна в этом пространстве, если любой элемент этого пространства может быть представлен в виде линейной комбинации элементов указанной системы либо в виде предела последовательности таких комбинаций.
. Система элементов нормированного пространства полна в этом пространстве, если любой элемент этого пространства может быть представлен в виде линейной комбинации элементов указанной системы либо в виде предела последовательности таких комбинаций.
Пространство, в котором можно указать конечный или счётный базаис, называется сепарабельным. Для нас важно, что пространство  сепарабельно.
сепарабельно.
Примеры базисов бесконечномерных пространств. Базисом линейного пространства 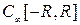 бесконечно дифференцируемых наотрезке
бесконечно дифференцируемых наотрезке 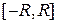 функций
функций 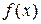 является система
является система 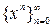 (здесь
(здесь 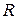 - наименьший радиус сходимости функций, принадлежащих данному пространству). Базисом линейного пространства
- наименьший радиус сходимости функций, принадлежащих данному пространству). Базисом линейного пространства 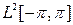 (с его среднеквадратичной метрикой) является, например, система
(с его среднеквадратичной метрикой) является, например, система 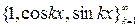 .
.
В некоторых случаях в  могут быть более удобными другие базисы (например, системы ортогональных полиномов).
могут быть более удобными другие базисы (например, системы ортогональных полиномов).
Множество конечных линейных комбинаций элементов такого базиса плотно в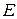 . Это значит, что для любого, сколь угодно малого
. Это значит, что для любого, сколь угодно малого 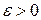 для произвольного элемента
для произвольного элемента 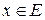 можно указать такую конечную линейную комбинацию
можно указать такую конечную линейную комбинацию 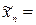
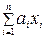 , что будет выполняться условие
, что будет выполняться условие 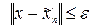 . Иначе говоря, можно подобрать такую конечную линейную комбинацию элементов этого базиса, которая будет сколь угодно близка к указанному элементу
. Иначе говоря, можно подобрать такую конечную линейную комбинацию элементов этого базиса, которая будет сколь угодно близка к указанному элементу 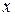 ; в численных методах обычно для этого требуется достаточно большое
; в численных методах обычно для этого требуется достаточно большое 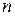 .
.
Если из базиса какого-либо пространства вычеркнуть элемент, мы не сможем аппроксимировать с любой точностью любой элемент этого пространства. Если же к базису дописать ещё один элемент этого пространства, полученная система будет линейно зависимой, и этот элемент не добавит базису никаких новых возможностей (он итак позволял описать любой элемент пространства). В этом смысле базис может быть назван минимальной системой.
Очень важную роль в прикладной математике играют базисы, которые называют ортогональными. Примерами ортогональных базисов являются: система ортов 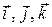 трёхмерного пространства, знакомого нам из векторной алгебры и аналитической геометрии; система
трёхмерного пространства, знакомого нам из векторной алгебры и аналитической геометрии; система  , используемая в рядах Фурье. Применение таких базисов в большом количестве случаев оказывается очень удобным, и прежде всего потому, что каждый коэффициент при орте в разложении по ортам определяется независимо. Система коэффициентов получается единственной и соответствующая линейная комбинация ортов даёт единственный элемент.
, используемая в рядах Фурье. Применение таких базисов в большом количестве случаев оказывается очень удобным, и прежде всего потому, что каждый коэффициент при орте в разложении по ортам определяется независимо. Система коэффициентов получается единственной и соответствующая линейная комбинация ортов даёт единственный элемент.


Для ортогональной системы это означает, что в 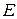 нет элемента, который нельзя было бы разложить в линейную комбинацию её элементов, то-есть, что она полна в
нет элемента, который нельзя было бы разложить в линейную комбинацию её элементов, то-есть, что она полна в 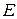 в обычном смысле ( в смысле определения 3.15).
в обычном смысле ( в смысле определения 3.15).
Почти всегда при численном решении краевых задач явно или без специального упоминания используется понятие проекции элемента в подпространство.

Говорят, что элемент 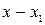 ортогонален к подпространству
ортогонален к подпространству 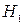 .
.
Для применения очень мощных прямыхчисленных методов важно понятие энергетического произведения. Действительно, при формулировании этих методов требуется определять скалярное произведение 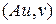 ,
, 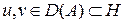 , где
, где 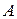 - положительно определённый самосопряжённый оператор. Он действует из
- положительно определённый самосопряжённый оператор. Он действует из 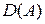 в
в 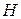 ,
,  - гильбертово пространство,
- гильбертово пространство, 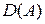 - область определения оператора
- область определения оператора 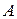 . Оператор, удовлетворяющий условию
. Оператор, удовлетворяющий условию 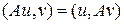
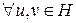 (обычно также требуют, чтобы он был ограниченным, то-есть, чтобы существовало такое вещественное
(обычно также требуют, чтобы он был ограниченным, то-есть, чтобы существовало такое вещественное 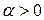 , что
, что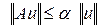 ,
, 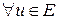 ), называется самосопряжённым. Положительно определённым он называется в случае, если
), называется самосопряжённым. Положительно определённым он называется в случае, если 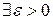 такое, что
такое, что 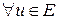
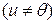 справедливо соотношение
справедливо соотношение 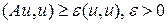 .
.
|
Можно доказать, что энергетическое произведение удовлетворяет определению скалярного произведения, попросту, также является скалярным призведением. Если на множестве 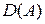 в качестве скалярного произведения ввести энергетическое произведение, то мы получим новое евклидово пространство, в общем случае не обязательно полное. Для того, чтобы исследовать сходимость последовательностей его элементов, на нём нужно ввести норму. Она вводится по аналогии с обычной нормой.
в качестве скалярного произведения ввести энергетическое произведение, то мы получим новое евклидово пространство, в общем случае не обязательно полное. Для того, чтобы исследовать сходимость последовательностей его элементов, на нём нужно ввести норму. Она вводится по аналогии с обычной нормой.
| |||
 |
Энергетическая норма одновременно может служить (и является) обычной нормой и, в частности, может использоваться при определении сходимости последовательностей.
Для построения численных методов необходимо, чтобы пространство, которому принадлежат все получаемые последовательности, было замкнутым (чтобы пределы всех получаемых последовательностей принадлежали тому же пространству). Поэтому принято добавлять: «Полученное евклидово пространство пополняем пределами всех его сходящихся последовательностей», хотя это не всегда легко осуществимо в численно анализе, но часто выполняется автоматически. Полученное замыкание  в энергетической норме является гильбертовым пространством и называется энергетическим пространством оператора
в энергетической норме является гильбертовым пространством и называется энергетическим пространством оператора 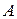 .
.
Введенные определения скалярого произведения произведения, нормы и сходимости используются при построении численных методов решения краевых задач для дифференциальны уравнений строительной механики в обыкновенных и частных производных и анализе условий сходимости последовательности решений при при увеличении длины отрезка координатной системы, используемого для аппроксимации их решения.

Энергетическое пространство оператора 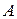 обозначается
обозначается 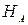 .
.
Это понятие чрезвычайно важно для численных методов, так как используемые в них системы элементов должны принадлежать энергетическому пространству дифференциального оператора левой части дифференциального уравнения задачи. Кроме того, как мы позже увидим, эти системы должны быть полны в 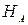 и любые их конечные подсистемы дожны быть линейно независимыми.
и любые их конечные подсистемы дожны быть линейно независимыми.
| <== предыдущая страница | | | следующая страница ==> |
| ММ-3. ПОНЯТИЯ, ИСПОЛЬЗУЕМЫЕ В ЧИСЛЕНЫХ МЕТОДАХ РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ОБЫКНОВЕННЫХ И ЧАСТНЫХ ПРОИЗВОДНЫХ | | | Критерии усвоения |
Дата добавления: 2014-04-15; просмотров: 524; Нарушение авторских прав

Мы поможем в написании ваших работ!
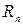 (Адрес файла Блок 4____)
Подпространством в
(Адрес файла Блок 4____)
Подпространством в 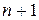 его элементов линейно зависимы, то число
его элементов линейно зависимы, то число 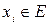 , которое каждый элемент
, которое каждый элемент 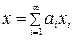 , причём это представление единственнои должно пониматься по аналогии с тем, как понимается сумма ряда.
Вернитесь к тексту
, причём это представление единственнои должно пониматься по аналогии с тем, как понимается сумма ряда.
Вернитесь к тексту
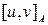 элементов
элементов 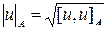 .
Вернитесь к тексту
.
Вернитесь к тексту