
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Приведенная форма системы эконометрических
Классификация систем эконометрических уравнений
Экономические явления обычно описываются не одной, а несколькими зависимостями, которые образуют систему уравнений.
В зависимости от того, как взаимосвязаны между собой зависимые и независимые переменные, различают три класса систем уравнений:
1. Система независимых уравнений, когда каждая зависимая переменная (у) является функцией одного и того же набора факторов (х).
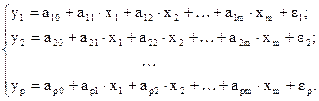
Каждое уравнение такой системы может рассматриваться самостоятельно. Для нахождения его параметров используется МНК. Каждое уравнение является уравнением регрессии.
2. Система рекурсивных уравнений, когда каждая зависимая переменная (у) одного уравнения выступает в виде фактора в другом уравнении:
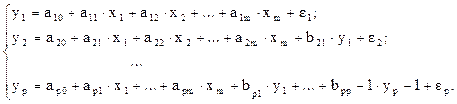
В данной системе уравнений каждое последующее уравнение включает предыдущие зависимые переменные. Однако, как и в предыдущем случае, каждое уравнение может рассматриваться самостоятельно, и его параметры определяются с помощью МНК.
3. Система взаимозависимых (совместных, одновременных) уравнений, в которой одни и те же зависимые переменные из одних уравнений входят во все другие уравнения:
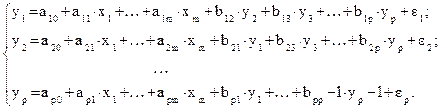
В эконометрике эта система уравнений называется также структурной формой модели. В отличие от предыдущих систем, каждое уравнение системы не может рассматриваться самостоятельно. Для нахождения его параметров традиционный МНК не применим. Используются специальные приемы оценивания параметров. Обычно все переменные модели выражаются в отношениях от среднего уровня, т.е. вместо х используется 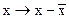 , а вместо
, а вместо 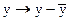 . Поэтому в уравнениях отсутствует свободный член:
. Поэтому в уравнениях отсутствует свободный член:
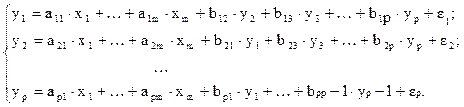
| <== предыдущая страница | | | следующая страница ==> |
| Метод наименьших модулей отклонений | | | Взаимозависимых уравнений |
Дата добавления: 2014-03-19; просмотров: 368; Нарушение авторских прав

Мы поможем в написании ваших работ!