Надежность компонентов оборудования

№ п/п	Компоненты оборудования	Интенсивность потока отказов 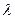, 10-3 лет (В.Маршал)	Интенсивность потока отказов 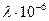, ч-1 ГОСТ 12.1.004-91	Вероятность отказа в течение года
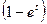
1.	Арматура трубопроводов (петлевые компенсаторы, тройники и вводы)			0,295
2.	Вентили			0,229
3.	Вращающиеся части насосов или смесителей			0,058
4.	Расширительные камеры			0,039
5.	Переходные шланги под давлением, втулки Шланги гибкие		3,93 0,067	0,034 5,867·10-4
6.	Емкости под давлением			0,017
7.	Прокладки			3,992·10-3
8.	Силовые линии			1,998·10-3
9.	Трубопроводы		1,1	9,59·10-3
10.	Манометры		1,3	0,011
11.	Прокладки: пластмассовые резиновые пробковые		0,05 0,04 0,02	4,379·10-4 3,503·10-4 1,752·10-4
12.	Сильфоны		2,287	0,02
13.	Соединения гидравлические		0,03	2,628·10-4
14.	Соединения пневматические		0,04	3,503·10-4
15.	Задвижки клапанов		5,1	0,044
16.	Клапаны: рычажные шариковые		4,6 4,6	0,0395 0,0395
17.	Клапаны дренажные		0,224	1,96·10-3
18.	Насосы с машинным приводом		8,74	0,074
19.	Моторы гидравлические		4,3	0,037
20.	Резервуары гидравлические		0,15	1,313·10-3
21.	Регуляторы давления		4,25	0,037
22.	Предохранительные мембраны		0,0112	9,811·10-5
23.	Индикаторы взрывов автоматических систем подавления взрывов		0,25	2,188·10-3
24.	Блоки управления автоматических систем подавления взрывов (на каждый канал)		0,12	1,051·10-3
25.	Пламеотсекатели ПО (АСПВ)		0,39	3,411·10-3
26.	Гидропушки ГП (АСПВ)		0,27	2,362·10-3
27.	Оросители АС (АСПВ)		0,32	2,799·10-3
28.	Кабели		0,047	4,116·10-4

Для нормального закона распределения плотность вероятности равна:

,

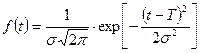(1.1)

где: 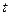и 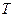- текущая и средняя (математическое ожидание) наработки до отказа;

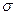- дисперсия.

Выражение 1.1 можно истолковать графически: вероятность появления отказа на наработку 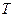, меньшую требуемой 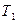, равна относительной площади под кривой 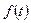слева от значения 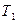(рис. 1.2).

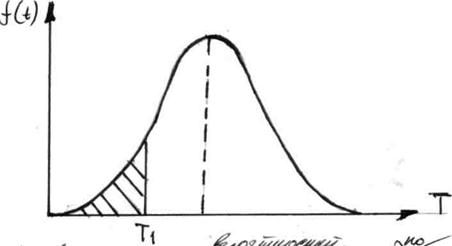
Рис. 1.2. Кривая плотности вероятностей распределения по нормальному закону.

Вероятность безотказной работы при нормальном распределении 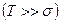определяется по формуле:

,

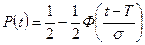где: 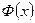- функция Лапласа;

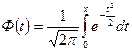- интеграл вероятности.

Вероятность отказа при нормальном распределении равна:

.

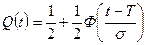Вероятность безотказной работы системы равна:

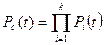
где: 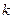- число элементов системы;

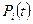- вероятность безотказной работы 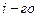элемента.

Вероятность отказа такой системы:

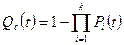или ,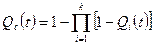

где 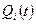- вероятность отказа 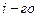элемента.

В случае экспоненциального закона надежности вероятность безотказной работы системы:

.

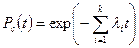Величину 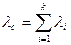называют интенсивностью отказов системы, состоящей из 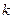элементов. Среднее время 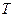такой системы:

,

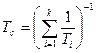где - среднее время работы элемента.

Вероятность безотказной работы при экспоненциальном законе распределения определяется формулой:

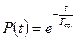или .

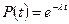Вероятность отказа при экспоненциальном законе распределения равна

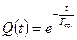или .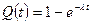

При функции надежности вида 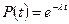частота отказов соответствует дискретному распределению Пуассона:

,

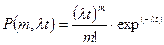где .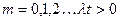

Аварии на временном интервале 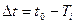произойдут 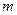раз с вероятностью 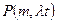, а отсутствие аварийных ситуаций (отсутствие отказов) с вероятностью .

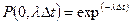Вероятность того, что аварии произойдут 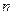раз при 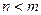(т.е. менее 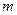раз) определяется функцией распределения:

,

.

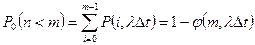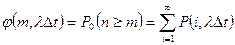Вероятность возникновения хотя бы одной аварии представляет оценку риска аварии на объекте за период :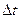

.

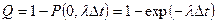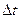Для оценки вероятности хотя бы одной аварии среди объектов за время указанное выражение примет вид:

.

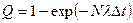Параметр потока аварий 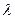(или вероятность аварии за данный промежуток времени) служит самостоятельным оценочным показателем опасности возникновения аварии и вычисляется с помощью выражения:

.

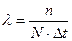Угрозу жизни человека при аварии (опасность летального исхода) оценивают «индивидуальным риском»:

,

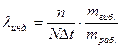где: 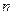- число объектов, на которых произошла авария за период ;

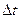- число эксплуатируемых объектов за тот же период;

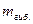- среднее число погибших на одном объекте при аварии;

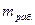- среднее число работающих на одном объекте.

Дата добавления: 2014-03-22; просмотров: 363; Нарушение авторских прав

Мы поможем в написании ваших работ!