
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Расчёт сопротивления грунтов
План лекции
После назначения глубины заложения подошвы фундамента приступают к определению ее основных размеров. В условиях нормальной эксплуатации зданий напряжения от внешней нагрузки под подошвой фундамента принимают равными расчетному сопротивлению грунта основания. В этом случае вводят соответствующие коэффициенты теории предельных состояний:
 (6.1.)
(6.1.)
где 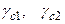 – коэффициенты условий работы соответственно грунтового основания и здания или сооружения во взаимодействии с основанием;
– коэффициенты условий работы соответственно грунтового основания и здания или сооружения во взаимодействии с основанием;
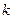 – коэффициент (
– коэффициент ( 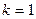 , если расчетные характеристики
, если расчетные характеристики 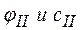 получены в результате непосредственного испытания образцов грунта строительной площадки;
получены в результате непосредственного испытания образцов грунта строительной площадки; 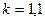 , если они получены по косвенным данным);
, если они получены по косвенным данным);
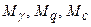 – безразмерные коэффициенты, зависящие от угла внутреннего трения;
– безразмерные коэффициенты, зависящие от угла внутреннего трения;
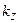 – коэффициент, принимаемый равным: при
– коэффициент, принимаемый равным: при 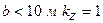 ; при
; при 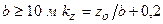 (здесь
(здесь 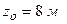 );
);
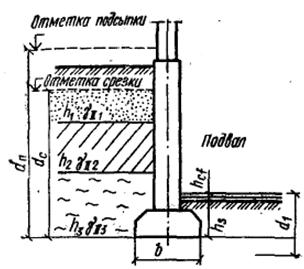
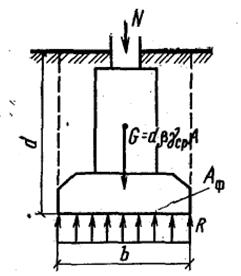
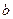 – меньшая ширина (сторона) подошвы фундамента (рис. 6.1);
– меньшая ширина (сторона) подошвы фундамента (рис. 6.1);
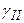 – осредненный расчетный удельный вес грунтов, залегающих ниже подошвы фундамента (при наличии грунтовых вод определяется с учетом взвешивающего действия воды);
– осредненный расчетный удельный вес грунтов, залегающих ниже подошвы фундамента (при наличии грунтовых вод определяется с учетом взвешивающего действия воды);
 – осредненный (по слоям) удельный вес грунта, залегающего выше отметки заложения фундамента (см. рис. 6.1)*, определяемый по формуле
– осредненный (по слоям) удельный вес грунта, залегающего выше отметки заложения фундамента (см. рис. 6.1)*, определяемый по формуле
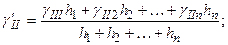 (6.2)
(6.2)
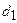 – глубина заложения фундаментов бесподвальных сооружений или приведенная глубина заложения наружных и внутренних фундаментов от пола подвала;
– глубина заложения фундаментов бесподвальных сооружений или приведенная глубина заложения наружных и внутренних фундаментов от пола подвала;
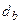 – глубина подвала – расстояние от уровня планировки до пола подвала; для сооружений с подвалом шириной
– глубина подвала – расстояние от уровня планировки до пола подвала; для сооружений с подвалом шириной 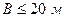 и глубиной более 2 м принимается
и глубиной более 2 м принимается 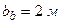 ; при ширине подвала
; при ширине подвала 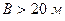 принимается
принимается 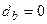 **;
**;
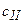 – расчетное удельное сцепление грунта, залегающего непосредственно под подошвой фундамента.
– расчетное удельное сцепление грунта, залегающего непосредственно под подошвой фундамента.
Величину 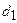 определяют по формуле
определяют по формуле
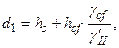 (6.3)
(6.3)
где 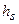 – толщина слоя грунта, залегающего выше подошвы фундамента со стороны подвала;
– толщина слоя грунта, залегающего выше подошвы фундамента со стороны подвала;
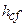 – толщина конструкции пола подвала;
– толщина конструкции пола подвала;
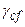 – расчетный удельный вес конструкции пола подвала ***.
– расчетный удельный вес конструкции пола подвала ***.
_______
* В случае однородного основания принимается 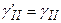 .
.
** При отсутствии подвала 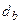 .
.
*** Расчетные значения удельного веса грунтов и материала пола подвала, входящие в формулу (6.1), допускается принимать равными их нормативным значениям.
| |||
| |||
Заметим, что индекс II в формуле (6.1) означает, что она используется в расчетах по второй группе предельных состояний. Кроме того, в случае отсутствия расчетных значений 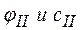 при проектировании фундаментов зданий и сооружений II–IV классов надежности. Строительными нормами допускается назначать их по косвенным данным с помощью специальных таблиц, т.е. принимать расчетные значения угла внутреннего трения и сцепления грунта равными их нормативным значениям (
при проектировании фундаментов зданий и сооружений II–IV классов надежности. Строительными нормами допускается назначать их по косвенным данным с помощью специальных таблиц, т.е. принимать расчетные значения угла внутреннего трения и сцепления грунта равными их нормативным значениям ( 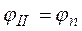 и
и 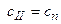 ).
).
Выбор формы подошвы фундамента зависит в основном от очертания возводимой конструкции в плане. Подошва может быть круглой, кольцевой, многоугольной, квадратной, прямоугольной, ленточной и т.п.
Основная трудность при проектировании фундаментов заключается в том, что их размеры назначают, исходя из расчетного сопротивления грунтов основания, в то время как оно является переменной величиной и, в свою очередь, зависит от размеров подошвы фундаментов [первое слагаемое, стоящее в скобках формулы (6.1.) зависит от 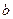 – ширины подошвы фундамента].
– ширины подошвы фундамента].
Напряжения по подошве фундамента определяют по формулам сопротивления материалов. При центральном действии нагрузки площадь фундамента 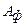 находят из условия равновесия всех сил, приложенных к нему (рис. 6.2):
находят из условия равновесия всех сил, приложенных к нему (рис. 6.2):
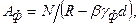 (6.4)
(6.4)
где 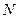 – внешняя нагрузка при коэффициенте надежности по нагрузке
– внешняя нагрузка при коэффициенте надежности по нагрузке 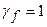 ;
;
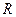 – расчетное сопротивление грунта основания;
– расчетное сопротивление грунта основания;
 – коэффициент, учитывающий меньший удельный вес грунта, лежащего на обрезах фундамента, по сравнению с удельным весом материала фундамента
– коэффициент, учитывающий меньший удельный вес грунта, лежащего на обрезах фундамента, по сравнению с удельным весом материала фундамента 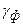 (в практических расчетах принимают
(в практических расчетах принимают 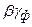 кН/м3);
кН/м3);
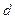 – глубина заложения фундамента.
– глубина заложения фундамента.
Как уже отмечалось выше, расчетное сопротивление грунта основания 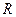 ,входящее в формулу (6.4), есть неизвестная величина, поэтому расчет ведется с помощью последовательных приближений. При этом в первом приближении принимают
,входящее в формулу (6.4), есть неизвестная величина, поэтому расчет ведется с помощью последовательных приближений. При этом в первом приближении принимают 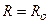 ,где
,где 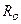 – условное расчетное сопротивление грунтов основания, назначаемое на основе данных инженерно-геологических изысканий на строительной площадке. В последующих приближениях величину
– условное расчетное сопротивление грунтов основания, назначаемое на основе данных инженерно-геологических изысканий на строительной площадке. В последующих приближениях величину 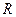 определяют по формуле (6.1) и сравнивают с напряжениями под подошвой фундамента, полученными по расчету, в данном приближении.
определяют по формуле (6.1) и сравнивают с напряжениями под подошвой фундамента, полученными по расчету, в данном приближении.
Для ленточных фундаментов расчет ведется на 1 м длины, следовательно, его ширина 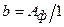 ; для фундаментов с прямоугольной подошвой предварительно задаются соотношением сторон
; для фундаментов с прямоугольной подошвой предварительно задаются соотношением сторон 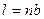 , тогда ширина подошвы
, тогда ширина подошвы 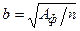 ; для круглых фундаментов
; для круглых фундаментов 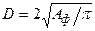 , а для квадратных –
, а для квадратных – 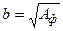 .
.
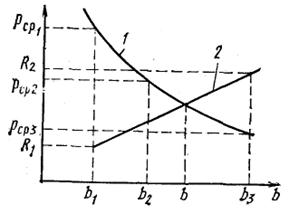
У фундаментов, для которых заранее неизвестно расчетное сопротивление грунта основания, размеры подошвы можно определить графическим способом. Среднее давление по подошве центрально-сжатого фундамента вычисляют по формуле
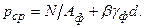 (6.5)
(6.5)
Для ленточного фундамента это выражение представляет собой гиперболу 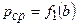 относительно аргумента
относительно аргумента 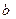 , а для прямоугольного – параболу
, а для прямоугольного – параболу 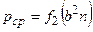 . Формула (6.1) является уравнением прямой
. Формула (6.1) является уравнением прямой 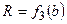 , поэтому значение искомой величины можно получить из совместного решения уравнений (6.1) и (6.5) графическим способом. Кривую 1 получают, задаваясь несколькими произвольными (обычно тремя) значениями
, поэтому значение искомой величины можно получить из совместного решения уравнений (6.1) и (6.5) графическим способом. Кривую 1 получают, задаваясь несколькими произвольными (обычно тремя) значениями 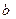 ,прямую 2 строят по двум точкам, задаваясь двумя произвольными значениями
,прямую 2 строят по двум точкам, задаваясь двумя произвольными значениями 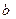 .Точка пересечения этих линий на графике и даст искомое значение ширины подошвы фундамента (рис. 6.3).
.Точка пересечения этих линий на графике и даст искомое значение ширины подошвы фундамента (рис. 6.3).
Давление под подошвой внецентренно нагруженных фундаментов определяют исходя из формул сопротивления материалов при внецентренном действии нагрузки (рис. 6.4):
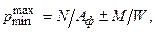 (6.6)
(6.6)
где 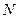 – вертикальная сила;
– вертикальная сила;
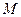 – момент на уровне подошвы фундамента;
– момент на уровне подошвы фундамента;
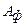 – площадь подошвы фундамента;
– площадь подошвы фундамента;
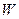 – момент сопротивления подошвы фундамента.
– момент сопротивления подошвы фундамента.
Величины 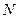 и
и 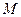 находят по формулам:
находят по формулам:
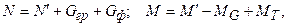
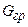 и
и 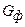 – вес соответственно фундамента и грунта на его обрезах;
– вес соответственно фундамента и грунта на его обрезах;
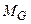 – момент относительно центра подошвы фундамента от веса обратной засыпки;
– момент относительно центра подошвы фундамента от веса обратной засыпки;
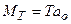 – момент от горизонтального давления грунта, здесь
– момент от горизонтального давления грунта, здесь
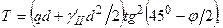 (6.7)
(6.7)
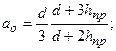 (6.8)
(6.8)
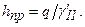
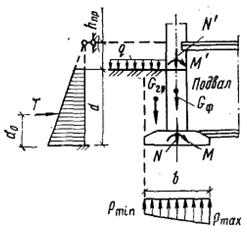
| Рис. 6.3. Графический способ определения ширины подошвы фундамента | Рис. 6.4. Расчетная схема внецентренно нагруженного фундамента |
Если перекрытия располагаются выше поверхности земли, то принимают 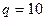 кН/м2.
кН/м2.
Для прямоугольных в плане фундаментов после подстановки в формулу (6.6) значений 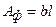 ,
, 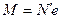 (
( 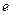 – эксцентриситет приложения силы
– эксцентриситет приложения силы 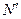 ) и
) и 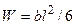 получим
получим
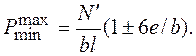 (6.9)
(6.9)
Заметим, что в формуле (6.9) не учитывают усилия от веса фундамента и обратной засыпки грунта.
Для внецентренно нагруженных фундаментов установлены следующие ограничения:
 (6.10)
(6.10)
Если в ходе расчетов окажется, что эксцентриситет приложения продольной силы 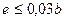 , то такой фундамент можно рассчитывать как центрально-сжатый.
, то такой фундамент можно рассчитывать как центрально-сжатый.
| <== предыдущая страница | | | следующая страница ==> |
| Фундаменты возводимые в открытых котлованах | | | Расчёт железобетонных фундаментов |
Дата добавления: 2014-05-28; просмотров: 1662; Нарушение авторских прав

Мы поможем в написании ваших работ!