Сети Петри

Сети Петри – аппарат для моделирования динамических дискретных систем (преимущественно асинхронных параллельных процессов).

Сеть Петри определяется как четверка <P,T,I,O>, где Р и Т – конечные

множества позиций и переходов, I и О – множества входных и выходных функций. Другими словами, сеть Петри представляет собой двудольный ориентированный граф, в котором позициям соответствуют вершины, изображаемые кружками, а переходам – вершины, изображаемые утолщенными черточками; функциям I соответствуют дуги, направленные от позиций к переходам, а функциям О – от переходов к позициям.

Как и в системах массового обслуживания, в сетях Петри вводятся объекты двух типов: динамические – изображаются метками (маркерами) внутри позиций и статические – им соответствуют вершины сети Петри.

Распределение маркеров по позициям называют маркировкой. Маркеры могут перемещаться в сети. Каждому условию в сети Петри соответствует определенная позиция. Совершению события соответствует срабатывание (возбуждение или запуск) перехода, при котором маркеры из входных позиций этого перехода перемещаются в выходные позиции. Последовательность событий образует моделируемый процесс.

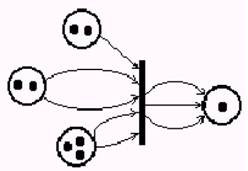
Рис.15.8. Сеть Петри

Правила срабатывания переходов (рис. 15.8), конкретизируют следующим образом: переход срабатывает, если для каждой из его входных позиций выполняется условие Nii Ki, где Ni – число маркеров в i–й входной позиции, Ki – число дуг, идущих от i–й позиции к переходу; при срабатывании перехода число маркеров в i–й входной позиции уменьшается на Ki, а в j–й выходной позиции увеличивается на Mj, где Mj – число дуг, связывающих переход с j–й позицией.

На рисунке 15.8 показан пример распределения маркеров по позициям перед срабатыванием, эту маркировку записывают в виде (2,2,3,1).

После срабатывания перехода маркировка становится иной: (1,0,1,4).

Можно вводить ряд дополнительных правил и условий в алгоритмы моделирования, получая ту или иную разновидность сетей Петри.

Так, прежде всего полезно ввести модельное время, чтобы моделировать не только последовательность событий, но и их привязку ко времени. Это осуществляется приданием переходам веса – продолжительности (задержки) срабатывания, которую можно определять, используя задаваемый при этом алгоритм. Полученную модель называют временной сетью Петри.

Если задержки являются случайными величинами, то сеть называют стохастической. В стохастических сетях возможно введение вероятностей срабатывания возбужденных переходов. Так, на рис. 15.9представлен фрагмент сети Петри, иллюстрирующий конфликтную ситуацию – маркер в позиции p может запустить либо переход t1, либо переход t2. В стохастической сети предусматривается вероятностный выбор срабатывающего перехода в таких ситуациях.

Если задержки определяются как функции некоторых аргументов, которыми могут быть количества маркеров в каких–либо позициях, состояния некоторых переходов и т.п., то сеть называют функциональной.

Во многих задачах динамические объекты могут быть нескольких типов, и для каждого типа нужно вводить свои алгоритмы поведения в сети. В этом случае каждый маркер должен иметь хотя бы один параметр, обозначающий тип маркера. Такой параметр обычно называют цветом; цвет можно использовать как аргумент в функциональных сетях. Сеть Петри при этом называют цветной.

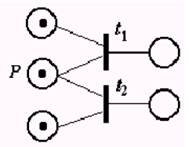
Рис.15.9. Конфликтная ситуация

Среди других разновидностей сетей Петри следует упомянуть ингибиторные сети, характеризующиеся тем, что в них возможны запрещающие (ингибиторные) дуги. Наличие маркера во входной позиции, связанной с переходом ингибиторной дугой, означает запрещение срабатывания перехода.

Поясним на следующих примерах.

1. Требуется описать с помощью сети Петри работу группы пользователей на единственной рабочей станции WS при заданных характеристиках потока запросов на пользование WS и характеристиках поступающих задач. Сеть Петри представлена на рис. 15.10.

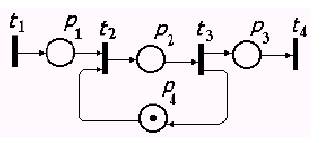
Рис.15.10. Сеть Петри для примера 1

Здесь переходы связаны со следующими событиями: t1 – поступление запроса на использование WS, t2 – занятие станции, t3 – освобождение станции, t4 – выход обслуженной заявки; позиция р4 используется для отображения состояния WS: если в р4 имеется метка, то WS свободна и пришедшая заявка вызывает срабатывание перехода t2; пока эта заявка не будет обслужена, метки в р4 не будет, следовательно, пришедшие в позицию «1» запросы вынуждены ожидать срабатывания перехода t3.

2. Требуется описать с помощью сети Петри процессы возникновения и устранения неисправностей в некоторой технической системе, состоящей из L однотипных блоков; в запасе имеется один исправный блок; известны статистические данные об интенсивностях возникновения отказов и длительностях таких операций, как поиск неисправностей, замена и ремонт отказавшего блока. На рис.15.11представлена соответствующая сеть Петри. Отметим, что при числе меток в позиции, равном M, можно в ней не ставить M точек, а записать в позиции значение M.

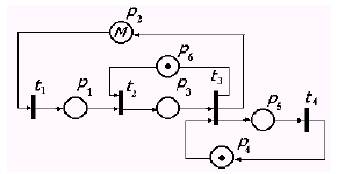
Рис.15.11. Сеть Петри для примера 2

В нашем примере значение M в позиции «2» соответствует числу имеющихся в системе блоков. Переходы отображают следующие события: t1 – отказ блока, t2 – поиск неисправного блока, t3 – его замена, t4 –окончание ремонта.

Очевидно, что при непустой позиции р2 переход t1 срабатывает, но с задержкой, равной вычисленному случайному значению моделируемого отрезка времени между отказами. После выхода маркера из t1 он попадает через р1 в t2, если имеется метка в позиции р6, это означает, что обслуживающая систему бригада специалистов свободна и может приступить к поиску возникшей неисправности. В переходе t2 метка задерживается на время, равное случайному значению длительности поиска неисправности. Далее маркер оказывается в р3 и, если имеется запасной блок (маркер в р4), то запускается переход t3, из которого маркеры выйдут в р2, р5 и в р6 через отрезок времени, требуемый для замены блока. После этого в t4 имитируется восстановление неисправного блока.

Рассматриваемая модель описывает функционирование системы в условиях, когда отказы могут возникать и в рабочем, и в неисправном состояниях системы. Поэтому не исключены ситуации, при которых более чем один маркер окажется в позиции р1.

Анализ сложных систем на базе сетей Петриможно выполнять посредством имитационного моделирования СМО, представленных моделями сетей Петри. При этом задают входные потоки заявок и определяют соответствующую реакцию системы. Выходные параметры СМО рассчитывают путем обработки накопленного при моделировании статистического материала.

Возможен и другой подход к использованию сетей Петри для анализа объектов, исследуемых на системном уровне. Он не связан с имитацией процессов и основан на исследовании таких свойств сетей Петри, как ограниченность, безопасность, сохраняемость, достижимость, живость.

Ограниченностьимеет место, если число меток в любой позиции сети не может превысить значения К. При проектировании автоматизированных систем определение К позволяет обоснованно выбирать емкости накопителей. Возможность неограниченного роста числа меток свидетельствует об опасности неограниченного роста длин очередей.

Безопасность– частный случай ограниченности, а именно это

1–ограниченность. Если для некоторой позиции установлено, что она

безопасна, то ее можно представлять одним триггером.

Сохраняемостьхарактеризуется постоянством загрузки ресурсов,

т.е.

ΣAiNi = const,

где Ni – число маркеров в i–й позиции, Ai – весовой коэффициент.

ДостижимостьMk→Mj характеризуется возможностью достижения маркировки Mj из состояния сети, характеризуемого маркировкой

Mk.

Живость сетиПетри определяется возможностью срабатывания любого перехода при функционировании моделируемого объекта. Отсутствие живости означает либо избыточность аппаратуры в проектируемой системе, либо свидетельствует о возможности возникновения зацикливаний, тупиков, блокировок.

В основе исследования перечисленных свойств сетей Петри лежит анализ достижимости.

Один из методов анализа достижимости любой маркировки из состояния Мо – построение графа достижимости. Начальная вершина графа отображает Мо, а остальные вершины соответствуют маркировкам. Дуга из Мi в Мj означает событие Mi→Mj и соответствует срабатыванию перехода t. В сложных сетях граф может содержать чрезмерно большое число вершин и дуг. Однако при построении графа можно не отображать все вершины, так как многие из них являются дублями (действительно, от маркировки Mk всегда порождается один и тот же подграф вне зависимости от того из какого состояния система пришла в Мk). Тупики обнаруживаются по отсутствию разрешенных переходов из какой–либо вершины, т.е. по наличию листьев – терминальных вершин. Неограниченный рост числа маркеров в какой–либо позиции свидетельствует о нарушениях ограниченности.

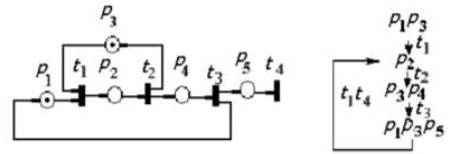
Рис.15.12. Сеть Петри и граф ее достижимости для примера 1

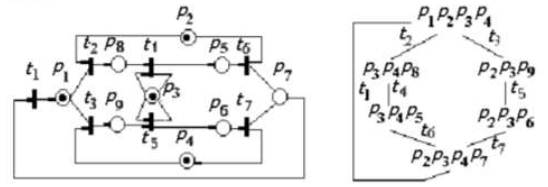
Рис.15.13. Сеть Петри и граф ее достижимости для примера 2

Дата добавления: 2014-02-26; просмотров: 1155; Нарушение авторских прав

Мы поможем в написании ваших работ!