Нормирование воздействия вибрации

Нормирование осуществляется по ГОСТ 12.1.012-90 «Вибрация. Общие требования безопасности» или по «СН 2.2.4/2.1.8.566–96. Производственная вибрация, вибрация в помещениях жилых и общественных зданий».

Определение предельно допустимых характеристик вибрации производится в зависимости от вида выполняемой работы. Сначала по известным виду выполняемой работы и месту её выполнения определяют категорию вибрации. Затем по категории вибрации находят предельно допустимое значение искомого параметра.

3.3.4.Защита от вибрации

Абсолютное большинство мероприятий, направленных на уменьшение вибрационного воздействия, так или иначе связано со снижением виброскорости. Поскольку нормируются среднеквадратичные значения виброскорости и виброускорения, то полезно знать связь между ними (для гармонических колебаний):

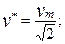
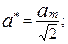
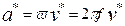
где: v_m и а_m - амплитудные значения виброскорости и виброускорения;

ω – угловая частота виброколебаний.

Для уяснения механизма действия тех или иных защитных мероприятий выведем уравнение, связывающее модуль амплитуды виброскорости с основными параметрами колебательной системы.

Согласно принципу д’Аламбера, уравнение, связывающее вибровозбуждающее усилие с параметрами колеблющейся под его воздействием системы, выглядит следующим образом:

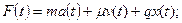, (3.9)

где: m – масса колеблющейся системы;

μ - коэффициент вязкого трения;

q – жесткость системы;

a(t), v(t), x(t) - соответственно виброускорение, виброскорость и вибросмещение от положения равновесия колебательной системы.

Для упрощения математических преобразований рассмотрим случай гармонических колебаний. Запишем закон изменения скорости во времени (в комплексном виде):

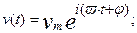
где: ω – угловая частота колебаний,

φ – начальная фаза колебаний.

Отсюда законы изменения виброускорения и вибросмещения:

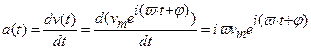(3.10)

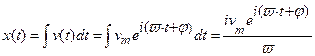(3.11)

Возмущающая сила также меняется по гармоническому закону:

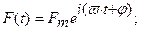(3.12)

Подставляя соотношения (3.10)÷(3.12) в уравнение (3.9) и сокращая на 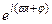получаем связь виброскорости с параметрами колеблющейся системы:

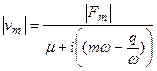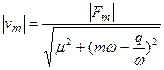; (3.13)

Дата добавления: 2014-08-04; просмотров: 299; Нарушение авторских прав

Мы поможем в написании ваших работ!