Если А есть В, то С есть К

А есть В

С есть К.

Покажем на примерах как в доказательствах можно явно выделять силлогизмы.

ТЕОРЕМА. Если в четырехугольнике противоположные стороны попарно равны, то такой четырехугольник является параллелограммом.

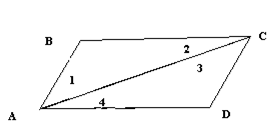
Доказательство. Проведем диагональ АС.

1-й силлогизм.

(Большая посылка) Если три стороны одного треугольника соответственно равны трем сторонам второго треугольника, то такие треугольники равны.

(Меньшая посылка) АС - общая сторона треугольников АВС и СДА; АВ=СД, ВС=ДА (по условию).

(Вывод) DАВС=DСДА.

2-й силлогизм.

(Б.п.) В равных треугольниках равны соответствующие углы.

(М.п.) Ð1 и Ð3 - соответствующие; Ð2 и Ð4 - соответствующие в равных треугольниках АВС и СДА.

(Вывод) Ð1 = Ð3, Ð2 = Ð4.

3-й силлогизм.

(Б.п.) Если при пересечении двух прямых третьей внутренние накрест лежащие углы равны, то эти две прямые параллельны.

(М.п.) Ð1 и Ð3 - равные и накрест лежащие при прямых АВ и СД, пересеченных прямой АС; Ð2 и Ð4 равные и накрест лежащие при прямых СВ и АД, пересеченных прямой АС.

(Вывод) АВêêСД и ВСêêАД.

4-й силлогизм.

(Б.п.) Четырехугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.

(М.п.) В четырехугольнике АВСД АВêêСД и ВСêêАД.

(Вывод) АВСД - параллелограмм.

Упражнение. Проведите доказательство следующей теоремы с использованием силлогизмов. В равнобедренном треугольнике углы при основании равны.

В качестве большей посылки силлогизма могут выступать ранее доказанные теоремы их следствия, аксиомы, а также определения. Меньшая посылка может включать в себя часть условия доказываемой теоремы или следствие, полученное из условия в предшествующих силлогизмах этого же доказательства.

В школьных учебниках по математике доказательства теорем не разбиты на силлогизмы. Учителю по возможности необходимо проводить работу со школьниками, направленную на преобразование книжных доказательств. Такая работа будет способствовать эффективному повторению, глубокому и прочному усвоению учебного материала, а также развитию творческого мышления.

Дата добавления: 2014-08-04; просмотров: 257; Нарушение авторских прав

Мы поможем в написании ваших работ!