Многократное измерение с неравноточными значениями отсчета

При многократном измерении с неравными значениями отсчета, подчиняющегося нормальному закону, функция правдоподобия может быть представлена в виде

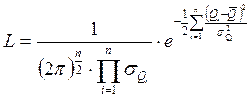
где все значения отсчета, полученные например, с помощью разных средств измерения, являются независимыми.

Для оценки среднего значения результата измерения прологарифмируем эту функцию и, выполнив математические преобразование получим:

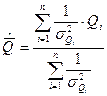
Это так называемое среднее взвешенное. В числителе отдельные значения результата измерения суммируются с «весами», обратно пропорциям их дисперсиям. Тем самым, более точным значениям придается больший вес.

Наличием суммы в знаменателе обеспечивается то, что в выражении

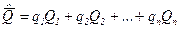
Сумма всех весов равна единице: 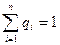, где нормированный вес каждого значения равен .

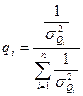Математическое ожидание среднего взвешенного 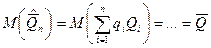. Т.о. среднее взвешенное является несмещенной оценкой среднего значения результата измерения.

Дата добавления: 2014-08-04; просмотров: 414; Нарушение авторских прав

Мы поможем в написании ваших работ!