Определение требуемой точности измерений

Многократное измерение одной и той же величины постоянного размера позволяют обеспечить требуемую точность. Поскольку ширина доверительного интервала зависит от количества экспериментов, то увеличивая n можно добиться выполнения наперед заданного условия .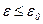

Пример

Имеется 10 независимых значений результата измерения линейного размера.

Определить длину с вероятностью 0,95. Точность измерения не ниже 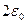=2см.

…	…

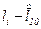
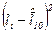
Решение

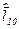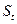1.Используя вспомогательные вычисления получим: =392, =2,5

2.Больше чем на 3 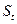=7,5 от среднего не отличается ни одно из значений. Следовательно ошибок нет.

3.Допустим есть основание полагать, что измерения подчиняются нормальному закону.

4.Стандартное отклонение среднего арифметического равно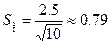

5.При 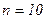Р=0,95 по графику распределения Стьюдента находим t=2,3.

6.Так как 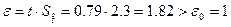, то необходимо увеличить количество экспериментальных данных.

7.Пусть 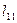=390, следовательно 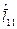=391,8 и 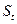=2,48.

8.Для проверки нормальности закона распределения используем составной критерий: при 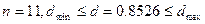и ни одно из численных значений 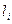не отличается от среднего больше чем на 2,5 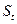. Т.о. результат проверки не противоречит гипотезе о нормальности.

9.Стандартное отклонение среднего арифметического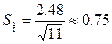

10. При 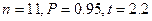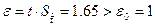, следовательно необходимо увеличивать количество экспериментальных данных. При таком задании .

На практике беспредельно повышать точность т.о. нельзя, т.к. рано или поздно определяющим становится не рассеяние расчета, а недостаток информации о поправках. Следовательно точность многократных измерений ограничивается дефицитом информации.

Дата добавления: 2014-08-04; просмотров: 289; Нарушение авторских прав

Мы поможем в написании ваших работ!