Виды и методы измерений. Качество измерений. Классификация погрешностей измерения. Расчет погрешностей измерения (начало)

Виды, методы и классы измерений.

Измерение — процесс, заключающийся в сравнении путем физического эксперимента данной ФВ с известной ФВ, принятой за единицу измерения.

Результатом процесса является значение физической величины Q = q[Q] , где q - числовое значение физической величины в принятых единицах; [Q] - единица физической величины. Значение физической величины Q, найденное при измерении, называют действительным.

Принцип измерений - физическое явление или совокупность физических явлений, положенных в основу измерений. Например, измерение массы тела при помощи взвешивания с использованием силы тяжести, пропорциональной массе, измерение температуры с использованием термоэлектрического эффекта.

Метод измерений - совокупность приемов использования принципов и средств измерений.

Средствами измерений (СИ) являются используемые технические средства, имеющие нормированные метрологические свойства.

По характеру зависимости измеряемой величины от времени измерения выделяют статические и динамические измерения.

Статические - это измерения, при которых измеряемая величина остается постоянной во времени. Такими измерениями являются, например, измерения размеров изделия, величины постоянного давления, температуры и др.

Динамические - это измерения, в процессе которых измеряемая величина изменяется во времени, например, измерение давления и температуры при сжатии газа в цилиндре двигателя.

По способу получения результатов, определяемому видом уравнения измерений, выделяют прямые, косвенные, совокупные и совместные измерения.

Прямые - это измерения, при которых искомое значение физической величины находят непосредственно из опытных данных.

Примерами таких измерений являются: измерение длины линейкой или рулеткой, измерение диаметра штангенциркулем или микрометром, измерение угла угломером, измерение температуры термометром и т.п.

Косвенные - это измерения, при которых значение величины определяют на основании известной зависимости между искомой величиной и величинами, значения которых находят прямыми измерениями.

Примеры косвенных измерений: определение объема тела по прямым измерениям его геометрических размеров, нахождение удельного электрического сопротивления проводника по его сопротивлению, длине и площади поперечного сечения.

Косвенные измерения широко распространены в тех случаях, когда искомую величину невозможно или слишком сложно измерить прямым измерением.

Встречаются случаи, когда величину можно измерить только косвенным путём, например размеры астрономического или внутриатомного порядка.

Совокупные - это такие измерения, при которых значения измеряемых величин определяют по результатам повторных измерений одной или нескольких одноименных величин при различных сочетаниях мер или этих величин. Значение искомой величины определяют решением системы уравнений, составляемых по результатам нескольких прямых измерений.

Примером совокупных измерений является определение массы отдельных гирь набора, т.е. проведение калибровки по известной массе одной из них и по результатам прямых измерений и сравнения масс различных сочетаний гирь.

Совместные - это измерения, производимые одновременно двух или нескольких разноименных величин для нахождения функциональной зависимости между ними.

Примерами совместных измерений являются определение длины стержня в зависимости от его температуры или зависимости электрического сопротивления проводника от давления и температуры.

Прямые измерения — основа более сложных измерений, и поэтому целесообразно рассмотреть методы прямых измерений. В соответствии с РМГ 29—99 различают:

1. Метод непосредственной оценки, при котором значение величины определяют непосредственно по отсчетному устройству измерительного прибора, например измерение давления пружинным манометром, массы — на весах, силы электрического тока — амперметром.

2. Метод сравнения с мерой, где измеряемую величину сравнивают с величиной, воспроизводимой мерой. Например, измерение массы на рычажных весах с уравновешиванием гирей; измерение напряжения постоянного тока на компенсаторе сравнением с ЭДС параллельного элемента.

3. Метод дополнения, если значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению.

4. Дифференциальный метод характеризуется измерением разности между измеряемой величиной и известной величиной, воспроизводимой мерой. Метод позволяет получить результат высокой точности при использовании относительно грубых средств измерения.

Пример 2.1.

Измерить длину х стержня, если известна длина l (l < х) меры. Как показано на рис. 2.3, x=l+а (а — измеряемая величина). Действительные значения а_д будут отличаться от измеренного а на величину погрешности Δ: a_д=а±Δ=а(1±Δ/а). Тогда x=l+a±Δ=(l+a)[l±Δ/(l+a)]. Поскольку l>>а, то Δ/(l+а)<<Δ/а.

Пусть Δ=0,1 мм; l=1000 мм; а=10 мм. Тогда 0.1/1010=0.0001(0,01%)<<0,1/10=0,01(1%).

5. Нулевой метод аналогичен дифференциальному, но разность между измеряемой величиной и мерой сводится к нулю. При этом нулевой метод имеет то преимущество, что мера может быть во много раз меньше измеряемой величины. Рассмотрим, например, неравноплечие весы, где P₁L₁=P₂L₂. В электротехнике — это мосты для измерения индуктивности, емкости, сопротивления. Здесь r₁∙r₂= r_x∙r₃, откуда r_x=r₁∙r₂/r₃. В общем случае совпадение сравниваемых величин регистрируется нуль-индикатором.

6. Метод замещения — метод сравнения с мерой, в которой измеряемую величину замещают известной величиной, воспроизводимой мерой. Например, взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов.

Кроме того, можно выделить нестандартизованные методы:

• метод противопоставления, при котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения. Например, измерения массы на равноплечих весах с помещением измеряемой массы и уравновешивающих ее гирь на двух чашках весов;

• метод совпадений, где разность между сравниваемыми величинами измеряют, используя совпадение отметок шкал или периодических сигналов.

Например, при измерении длины штангенциркулем наблюдают совпадение отметок на шкалах штангенциркуля и нониуса; при измерении частоты вращения стробоскопом — метки на вращающемся объекте с моментом вспышек известной частоты.

В литературе иногда встречается название измерений с однократными наблюдениями — обыкновенные измерения, с многократными — статистические. Кроме того, если весь измеряемый параметр фиксируется непосредственно СИ, то это — абсолютный метод, а если СИ фиксирует лишь отклонение параметра от установочного значения, то это относительный (пороговый) метод измерения.

По условиям, определяющим точность результата, измерения делятся на три класса.

1. Измерения максимально возможной точности, достижимой при существующем уровне техники. В этот класс включены все высокоточные измерения и в первую очередь эталонные измерения, связанные с максимально возможной точностью воспроизведения установленных единиц физических величин. Сюда относятся также измерения физических констант, прежде всего универсальных, например измерение абсолютного значения ускорения свободного падения.

2. Контрольно-поверочные измерения, погрешность которых с определенной вероятностью не должна превышать некоторого заданного значения. В этот класс включены измерения, выполняемые лабораториями государственного контроля (надзора) за соблюдением требований технических регламентов, а также состоянием измерительной техники и заводскими измерительными лабораториями. Эти измерения гарантируют погрешность результата с определенной вероятностью, не превышающей некоторого, заранее заданного значения.

3. Технические измерения, в которых погрешность результата определяется характеристиками средств измерений. Примерами технических измерений являются измерения, выполняемые в процессе производства на промышленных предприятиях, в сфере услуг и др.

Качество измерений.

Качество измерений характеризуется: точностью, достоверностью, правильностью, сходимостью и воспроизводимостью измерений, а также их стабильностью.

Различают результат наблюдения - значение величины, полученное при отдельном наблюдении, и результат измерения - значение величины, найденное в процессе измерения, после обработки результатов наблюдения.

Точность - это качество измерений, отражающее близость их результатов к истинному значению измеряемой величины.

Термин "точность измерений" не имеет строгого определения и используется для качественного сравнения измерительных операций. Для количественной оценки используется понятие "погрешность измерений" (чем меньше погрешность, тем выше точность).

Погрешность измерения Δх_изм — это отклонение результата измерения х от истинного (действительного) х_и(х_д) значения измеряемой величины:

Δх_изм= х-х_д.

Стабильность средства измерений - качественная характеристика средства измерений, отражающая неизменность во времени его метрологических свойств. В качестве количественной оценки стабильности служит нестабильность средства измерений или вариация его показаний.

Достоверность измерений характеризует степень доверия к результатам измерений. Достоверность оценки погрешностей определяют на основе законов теории вероятностей и математической статистики. Это дает возможность для каждого конкретного случая выбирать средства и методы измерений, обеспечивающие получение результата, погрешности которого не превышают заданных границ с необходимой достоверностью.

Правильность измерений - это качество измерений, отражающее близость к нулю систематических погрешностей в результатах измерений.

Сходимость - это качество измерений, отражающее близость друг к другу результатов измерений одного и того же параметра, выполненных повторно одними и теми же средствами одним и тем же методом в одинаковых условиях и с одинаковой тщательностью.

Воспроизводимость - это качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в различных условиях (в различное время, в различных местах, различными методами и средствами).

Классификация погрешностей измерения.

Количество факторов, влияющих на точность измерения, достаточно велико, и любая классификация погрешностей измерения в известной мере условна, так как различные погрешности в зависимости от условий измерительного процесса проявляются в различных группах. Поэтому для практических целей достаточно рассмотреть случайные и систематические составляющие общей погрешности, выраженные в абсолютных или относительных единицах.

В зависимости от формы выражения различают абсолютную, относительную и приведенную погрешности измерения.

Абсолютная погрешность определяется как разность

Δ=х-х_и или Δ=х-х_д,

Относительная погрешность определяется как отношение

δ = ±Δ/x∙100% или δ = ±Δ/x_д∙100%.

Приведенная погрешность

у=±Δ/x_n∙100% ,

где х_n— нормированное значение величины. Например, х_n= х_mах, где х_mах — максимальное значение измеряемой величины.

В зависимости от характера проявления, причин возникновения и возможностей устранения различают систематическую и случайную составляющие погрешности измерений, а также грубые погрешности (промахи).

· Систематическая погрешность измерения - составляющая погрешности измерения, остающаяся постоянной или изменяющаяся по определенному закону при повторных измерениях одной и той же величины. Систематическая погрешность может быть исключена с помощью поправки.

· Случайная погрешность - составляющая погрешности измерения, изменяющаяся при повторных измерениях одной и той же величины случайным образом.

· Грубая погрешность измерения - погрешность, значение которой существенно выше ожидаемой.

В отличие от случайной погрешности, выявленной в целом в, зависимости от ее источников, систематическая погрешность рассматривается по составляющим в зависимости от источников ее возникновения, причем различают методическую, инструментальную и субъективную составляющие погрешности.

Субъективные систематические погрешности связаны с индивидуальными особенностями оператора. Как правило, эта погрешность возникает из-за ошибок в отсчете показаний (примерно 0.5 деления шкалы) и неопытности оператора.

Возможны четыре вида субъективных погрешностей:

· погрешность отсчитывания;

· погрешность присутствия (проявляется в виде влияния теплоизлучения оператора на температуру окружающей среды, а тем самым и на измерительное средство);

· погрешность действия (вносится оператором при настройке прибора);

· профессиональные погрешности (связаны с квалификацией оператора, с отношением его к процессу измерения).

Методическая составляющая погрешности обусловлена несовершенством метода измерения, приемами использования СИ, некорректностью расчетных формул и округления результатов.

Инструментальная составляющая возникает из-за собственной погрешности СИ, определяемой классом точности, влиянием СИ на результат и ограниченной разрешающей способности СИ. Эта погрешность может быть разделена на несколько видов по причинам возникновения:

· инструментальная погрешность - составляющая погрешности измерения, зависящая от погрешностей применяемых средств. Эти погрешности определяются качеством изготовлении самих измерительных приборов.

· погрешность поверки - составляющая погрешности измерений, являющаяся следствием несовершенства поверки средств измерений.

· погрешности от измерительного усилия действуют в случае контактных измерительных приборов. При оценке влияния измерительного усилия на погрешность измерения, необходимо выделить упругие деформации установочного узла и деформации в зоне контакта измерительного наконечника с деталью.

· влияющая физическая величина - физическая величина, не измеряемая данным средством, но оказывающая влияние на результаты измеряемой величины, например: температура и давление окружающей среды; относительная влажность и др. отличные от нормальных значений.

Погрешность средства измерения, возникающая при использовании его в нормальных условиях, когда влияющие величины находятся в пределах нормальной области значений, называют основной.

Если значение влияющей величины выходит за пределы нормальной области значений, появляется дополнительная погрешность.

Нормальные условия применения средств измерений - условия их применения, при которых влияющие величины имеют, нормальные значения пли находятся в пределах нормальной (рабочей) области значений. Нормальные условия выполнения линейных и угловых измерений и поверки регламентированы соответственно ГОСТ 8.050-73 и ГОСТ 8.395-80.

Как правило, нормальными условиями эксплуатации являются: температура 293±5 К или 20±5°С, относительная влажность воздуха 65+15% при 20°С, напряжение в сети питания 220 В+10% с частотой 50 Гц±1%, атмосферное давление от 97,4 до 104 кПа, отсутствие электрических и магнитных полей (наводок).

Расчет погрешностей измерения.

Основы теории вероятностей для расчета случайных величин.

Появление того или иного числового значения случайной величины в результате измерений рассматривается как случайное событие. То же самое происходит при проведении, каких либо испытаний продукции, например, для установления его показателей качества.

Отношение числа n случаев появления случайной величины или события A к числу N всех произведенных испытаний, при которых это событие могло появиться, называют частостью, или относительной частотой W (А) = n/N.

При достаточно большом числе испытаний N обнаруживается устойчивость значения указанного отношения для большинства случайных событий. Величина W (A) для события А будет колебаться около некоторого постоянного числа, равного единице. Это число, всегда меньшее единицы, называют вероятностью Р (А) появления события А, т. е. Р (А) является мерой объективной возможноcти появления события А.

Вероятность достоверного события равна единице, невозможного события - нулю.

За приближенное значение вероятности Р (А) события А при достаточном числе испытаний можно принимать частость:

P (A ) ≈ W (A) = n/N (1)

Частость W (A) отличается от вероятности Р (A) тем, что представляет собой случайную величину, которая в различных сериях однотипных испытаний может принимать в зависимости от случайных факторов различные значения, тогда как вероятность Р (А) представляет постоянное для каждого данного события число, определяющее в среднем частость его появления в опытах.

По мере увеличения N частость приближается к вероятности.

Зависимость между числовыми значениями случайной величины и вероятностью их появления устанавливается законом распределения вероятностей случайных величин. Закон распределения вероятностей дискретной случайной величины можно представить в виде таблицы или графика, показывающего, с какой вероятностью случайная величина X принимает то или иное числовое значение xi.

Закон распределения вероятностей непрерывной случайной величины, которая может принимать любое значение в пределах заданного интервала нельзя представить в виде таблицы.

Закон распределения представляют в виде дифференциальной функции распределения или плотности распределения вероятности pX (x). Эта функция представляет собой предел отношения вероятности того, что случайная величина X примет значение, лежащее в интервале от x до х + Δx , к величине интервала Δх, при Δх, стремящемся к нулю.

Характер рассеяния достаточно большой совокупности значений случайной величины, как правило, соответствует определённому теоретическому закону распределения.

Рассеяние значений случайной величины, изменение которой зависит от большого числа факторов, когда ни один из факторов не имеет преобладающего влияния, подчиняется закону нормального распределения вероятностей (закону Гаусса), показанного на рис. 3.

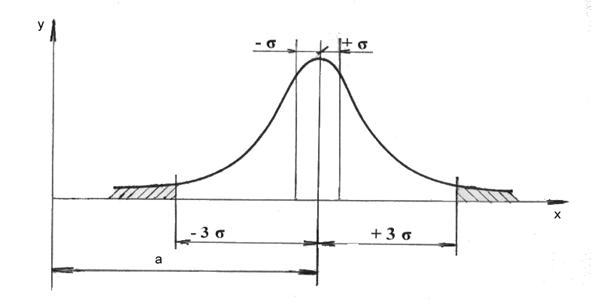
Рис. 3. Кривая плотности вероятности нормального распределения

Этому закону с некоторым приближением может подчиняться: рассеяние погрешностей многократных измерений; рассеяние погрешностей изготовления; погрешности измерения линейных и угловых размеров; массы деталей; величин твердости и других механических и физических величин.

Закон нормального распределения имеет следующие свойства:

· вероятность появления положительных и отрицательных погрешностей одинакова;

· малые по величине погрешности имеют большую вероятность появления, чем большие;

· алгебраическая сумма отклонений от среднего значения равна нулю.

Зависимость плотности вероятности определяется уравнением:

(2)

где a и σ- параметры распределения; x - аргумент функции плотности вероятности, т.е. случайная величина, изменяющаяся в пределах - ∞< x < +∞; e - основание натуральных логарифмов. Нормальное распределение представляет собой кривую симметричную относительно оси ординат. Величина a равна математическому ожиданию MX случайной величины X, определяемому по формулам:

для дискретной величины

(3),

где x_i - возможное значение дискретной случайной величины; p(x_i) - вероятность значения x_i дискретной случайной величины;

для непрерывных величин ,

(4),

где рX (х) - плотность вероятности непрерывной случайной величины X. Значение MX характеризует положение центра группирования случайных величин, около которого располагаются, например, размеры большинства деталей в партии.

При отсутствии систематических погрешностей в результатах многократных измерений одной и той же величины в одних и тех же условиях, математическое ожидание можно рассматривать как наибольшее приближение к истинному значению измеряемой величины.

Величину рассеяния значений случайной величины относительно центра группирования определяет параметр σ, который называют средним квадратическим отклонением случайной величины, его определяют по формулам:

для непрерывной величины

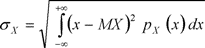(5)

для дискретной величины

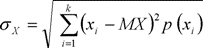(6)

Рассеяние случайных величин характеризуется также дисперсией

DX = σ²X. (14)

В тоже время существуют другие законы распределения, описывающие случайные величины, природа возникновения которых имеет несколько иной характер.

В рассматриваемом случае необходимо упомянуть закон Максвелла, которому подчиняются существенно положительные величины, например: рассеяние значений эксцентриситета, радиальное и торцевое биения, отклонения от соосности, дисбаланс и другие величин, которые не могут принимать отрицательные значения.

Для оценки надёжности работы изделий используют закон Вейбулла, который даёт представление о вероятности отказов.

Получили распространение также закон Симпсона или закон треугольника и закон равной вероятности.

Однако, для обработки результатов наблюдений в основном применяют закон нормального распределения - закон Гаусса.

Вернемся к распределению вероятностей Гаусса. Формула (2) выражает уравнение кривой, если начало отсчета расположено на оси x произвольно. При совпадении центра группирования с началом отсчета величины x уравнение кривой нормального распределения будет иметь вид

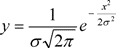(7)

Вероятность попадания величины в заданный интервал можно определить следующим образом. Ветви теоретической кривой нормального распределения (рис. 3) уходят в бесконечность, асимптотически приближаясь к оси абсцисс. Площадь, ограничиваемая кривой и осью абсцисс, равна вероятности того, что случайная величина, например, погрешность размера, лежит в интервале ±∞. Площадь под кривой распределения равна 1 или 100%, она определяется интегралом

(8)

Начало координат расположено в точке, совпадающей с центром группирования. Так как подынтегральная функция четная и кривая симметрична относительно максимальной ординаты, можно записать

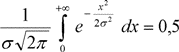(9)

Для выражения случайной величины x в долях ее σ примем: x/ σ = z, откуда x = σz, dx = σdz. В этом случае абсцисса на рис. 3.3 будет выражена в долях σ. Если принять за пределы интегрирования 0 и z, то интеграл в выражении (3.8) будет функцией z, т.е.

(10)

Функцию Ф0 (z) называют нормированной функцией Лапласа: Ф0 (0) = 0; Ф0 (- z) = - Ф0 (z); Ф0 (-∞) = - 0,5; Ф0 (+∞) = 0,5.

Из формулы (8) и рис. 4 следует, что площадь, ограниченная отрезком -z1 +z1 оси абсцисс, кривой плотности вероятности и двумя ординатами, соответствующими границам отрезка, представляет собой вероятность попадания случайной величины z1, в данный интервал.

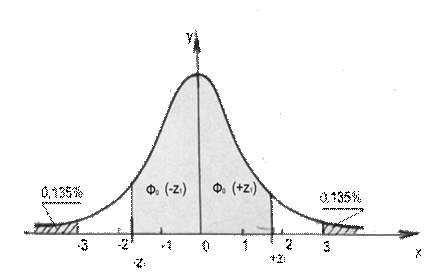
Рис. 4 Кривая нормального распределения и иллюстрация подынтегральных функций

Данные для функции Ф0(z) приводятся в справочниках. Пользуясь этими данными можно определить вероятность того, что случайная величина x, выраженная через σ, будет находиться в пределах того или иного интервала ±z1σ. Например, находим, при z1 = 3, что соответствует случайной величине x = 3σ, Ф0(3) = 0,49865 или Ф0(-3) - Ф0(3) = 2Ф0(3) = 0,9973.

Так как площадь, ограниченная кривой Гаусса и осью абсцисс, равна 1, то площадь, лежащая за пределами значений х = ±3σ, равна 1 - 0,9973 = 0,0027 и расположена симметрично по 0,00135 или по 0,135% справа и слева относительно оси у (см. рис. 4).

Следовательно, с вероятностью, близкой к единице, можно утверждать, что случайная величина X не будет выходить за пределы ±3σ. Поэтому при распределении случайной величины по закону Гаусса поле рассеяния, равно Vlim = 6σ или диапазон ±3σ считают за практически предельное поле рассеяния случайной величины и принимают за норму точности - допуск. При этом вероятность выхода случайной величины за пределы значений ±3σ равна 0,0027 или 0,27%.

Дата добавления: 2014-09-08; просмотров: 1901; Нарушение авторских прав

Мы поможем в написании ваших работ!