Расчет погрешностей измерения (окончание). Методы суммирования погрешностей. Нормирование погрешностей и формы представления результатов измерений

Определение величины случайных погрешностей.

Случайные погрешности нельзя исключить полностью, но их влияние может быть уменьшено путем обработки результатов измерений. Для этого должны быть известны вероятностные и статистические характеристики:

• закон распределения,
• закон математического ожидания,
• среднее квадратическое отклонение (СКО),
• доверительная вероятность и доверительный интервал.
1. Закон распределения.

Для предварительной оценки закона распределения параметра часто используют относительную величину СКО — коэффициент вариации:

или ( )

Например, при ν_х < 0,33,...,0,35 можно считать, что распределение случайной величины подчиняется нормальному закону.

1. Математическое ожидание.

В качестве математического ожидания при многократных измерениях параметра выступает среднее арифметическое значение .

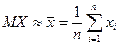(11)

При отсутствии систематических погрешностей в результатах многократных измерений одной и той же величины в одних и тех же условиях, математическое ожидание можно рассматривать как наибольшее приближение к истинному значению измеряемой величины.

1. Среднее квадратическое отклонение (СКО).

Тем не менее, величина , полученная в одной серии измерений, является случайным приближением к х_и. Для оценки ее возможных отклонений от х_и определяют опытное среднее квадратическое отклонение 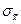(CKO)

(12)

Для оценки рассеяния отдельных результатов х измерения относительно среднего определяют СКО по формуле: (6):

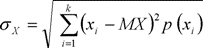
или, подставляя в них выражение (11):

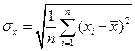при n≥20

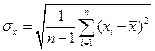при n<20 (13)

Формулы (12) и (13) соответствуют центральной предельной теореме теории вероятностей, согласно которой

(14)

Среднее арифметическое из ряда измерений всегда имеет меньшую погрешность, чем погрешность каждого определенного измерения. Из этого следует, что если необходимо повысить точность результата (при исключении систематической погрешности) в 2 раза, то число измерений нужно увеличить в 4 раза; если требуется увеличить точность в 3 раза, то число измерений увеличивают в 9 раз и т. д.

Нужно четко разграничивать применение формул (12) и (13): величина (13) используется при оценке погрешностей окончательного результата, а (12) — при оценке погрешности метода измерения.

1. Доверительная вероятность и доверительный интервал.

Если Р означает вероятность α того, что результата измерения отличается от истинного на величину не более чем 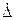, т.е.

, (15)

то в этом случае Р — доверительная вероятность, а интервал от 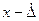до 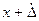— доверительный интервал. Таким образом, для характеристики случайной погрешности надо обязательно задать два числа — величину самой погрешности (или доверительный интервал) и доверительную вероятность.

Если распределение случайной погрешности подчиняется нормальному закону (а это как правило), то вместо значения 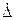указывается σ_x Одновременно это уже определяет и доверительную вероятность Р. Например: при 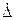= σ_x значение Р= 0,68; при 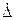= 2σ_x значение Р= 0,95; при 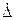= 3σ_x значение Р= 0,99 (см. основы теории вероятности выше).

Доверительная вероятность по формуле (15) характеризует вероятность того, что отдельное измерение х_i не будет отклоняться от истинного значения более чем на 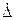. Безусловно, важнее знать отклонение от истинного значения среднего арифметического ряда измерений.

До сих пор рассматривались оценки СКО по "необходимому" (достаточно большому) числу измерений. В этом случае σ² называется генеральной дисперсией. При малом числе измерений (менее 10—20) получают так называемую выборочную дисперсию 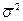. Причем 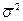→σ² лишь при n→∞. То есть если считать, что 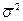=σ², то надежность оценки снижается с уменьшением n, а значения доверительной вероятности Р завышаются.

Поэтому при ограниченном числе измерений n вводят коэффициент Стьюдента t_p, определяемый по специальным таблицам (см ниже) в зависимости от числа измерений и принятой доверительной вероятности Р.

Тогда средний результат измерений находится с заданной вероятностью Р в интервале

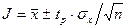(16)

и отличается от действительного значения на относительную величину

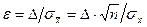. (17)

Случайная погрешность и количество измерениий.

Для уменьшения случайной погрешности есть два пути: повышение точности измерений (уменьшение σ_х) и увеличение числа измерений n с целью использования соотношения (14). Считая, что все возможности совершенствования техники измерений использованы, рассмотрим второй путь. При этом отметим, что уменьшать случайную составляющую погрешности целесообразно лишь до тех пор, пока общая погрешность измерений не будет полностью определяться систематической составляющей Δ_с. Если систематическая погрешность определяется классом точности СИ Δ_си (или γ_си), то необходимо, чтобы доверительный интервал 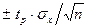был существенно меньше Δ_си.

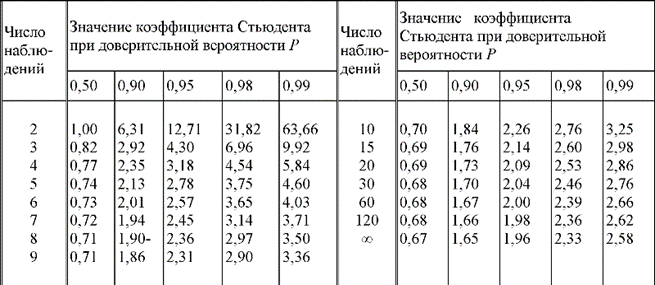
Обычно принимают от 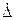<Δ_с/2 до 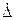<Δ_с/10 при Р=0,95. В случае невозможности выполнить эти соотношения необходимо коренным образом изменить методику измерения.

Для сравнения случайных погрешностей с различными законами распределения использование показателей, сводящих плотность распределения к одному или нескольким числам, обязательно. В качестве таких чисел и выступают СКО, доверительный интервал и доверительная вероятность.

Надежность самого СКО характеризуется величиной

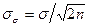. (18)

Принято, что если σ_σ≤0,25σ, то оценка точности надежна. Это условие выполняется уже при n=8.

Наиболее вероятная погрешность Δ_в отдельного измерения определяется по формуле

.

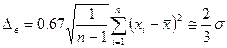Анализ этой формулы показывает, что с увеличением n величина Δ_в быстро уменьшается лишь до n=5 ... 10. Следовательно, увеличение числа измерений на одном режиме свыше 5... 10 нецелесообразно, что совпадает с условием получения надежных значений σ_σ.

Число измерений можно выбрать по одной из формул:

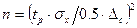или

где n_от — число отбрасываемых экспериментальных результатов.

С учетом коэффициентов Стьюдента можно оценить относительную погрешность отдельного измерения как , так и среднего значения .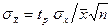

Определение систематических погрешностей.

Как правило, считают, что систематические погрешности могут быть обнаружены и исключены. Однако в реальных условиях полностью исключить систематическую составляющую погрешности невозможно. Всегда остаются какие-то неисключенные остатки, которые и нужно учитывать, чтобы оценить их границы. Это и будет систематическая погрешность измерения. То есть в принципе систематическая погрешность тоже случайна, и указание деление обусловлено лишь установившимися традициями обработки и представления результатов измерения.

Оставшаяся необнаруженной систематическая составляющая опаснее случайной: если случайная составляющая вызывает вариацию (разброс) результатов, то систематическая — устойчиво их искажает (смещает). В любом случае отсутствие или незначительность (с целью пренебрежения) систематической погрешности нужно доказать.

Действительно, если взять два ряда измерений одной и той же величины, то средние результаты этих рядов, как правило, будут различны. Это расхождение может быть определено случайной или систематической составляющей.

Методика выявления характера погрешности заключается в следующем:

1. Из двух рядов n₁ и n₂ независимых измерений находят средние арифметические х₁, и х₂.

2. Определяют значения

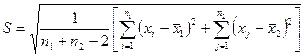
3. Вычисляют .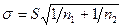

4. Вероятность того, что разность |x₁-х₂|>ε является случайной величиной, определяется равенством Р(|x₁-х₂|>ε)=1-Pt_pn где t_p=|x₁-х₂|/σ; n=n₁+n₂-2. Величина Р определяется по таблице Стьюдента.

Если полученная вероятность Р>0,95, то разность |x₁-х₂| носит систематический характер.

Пример.

Расчетные значения составили t_p=3 и n=15. По таблице Стьюдента находим, что при

n-1=14 и t_p=2,98≡3 величина Р=0,99. Тогда Р= 0,99 > 0,95, что свидетельствует о систематическом характере погрешности.

В отличие от случайной погрешности, выявленной в целом в, зависимости от ее источников, систематическая погрешность рассматривается по составляющим в зависимости от источников ее возникновения, причем различают методическую, инструментальную и субъективную составляющие погрешности.

Целесообразность разделения систематической погрешности на методическую и инструментальную составляющие определяется следующими моментами:

• для повышения точности измерений можно выделить лимитирующие факторы, а следовательно, принять решение об усовершенствовании методики или выборе более точных СИ;

• появляется возможность определить составляющую общей погрешности, увеличивающейся со временем или под влиянием внешних факторов, а следовательно, целенаправленно осуществлять периодические поверки и аттестации;

• инструментальная составляющая может быть оценена до разработки методики, а потенциальные точностные возможности выбранного метода определит только методическая составляющая.

То есть все виды составляющих погрешности нужно анализировать и выявлять в отдельности, а затем суммировать их в зависимости от характера, что является основной задачей при разработке и аттестации методик выполнения измерений.

В ряде случаев систематическая погрешность может быть исключена за счет устранения источников погрешности до начала измерений (профилактика погрешности), а в процессе измерений — путем внесения известных поправок в результаты измерений.

Профилактика погрешности — наиболее рациональный способ ее снижения и заключается в устранении влияния, например температуры (термостатированием и термоизоляцией), магнитных полей (магнитными экранами), вибраций и т. п. Сюда же относятся регулировка, ремонт и поверка СИ.

Исключение постоянных систематических погрешностей в процессе измерений осуществляют методом сравнения (замещения, противопоставления), компенсации по знаку (предусматривают два наблюдения, чтобы в результат каждого измерения систематическая погрешность входила с разным знаком), а исключение переменных и прогрессирующих — способами симметричных наблюдений или наблюдением четное число раз через полупериоды.

Методы суммирования погрешностей.

При нормировании точности технологического процесса или процесса измерения, а также при анализе действительной точности этих процессов возникает задача суммирования погрешностей, т.е. получение суммарной погрешности.

Возникает также задача разложения полученной в результате измерения суммарной погрешности на отдельные составляющие. Вторая задача является более сложной и не всегда имеет единственное, т. е. вполне определенное, решение.

Методы суммирования погрешностей различны в зависимости от вида погрешностей, т. е. в зависимости от того, являются ли погрешности величинами скалярными, векторными, постоянными или переменными, изменяющимися по экспоненциальному закону, убывающими, возрастающими или изменяющимися по периодическому закону.

Кроме того, следует различать, являются ли для данного процесса суммируемые погрешности случайнымиили систематическими.

1. Суммирование случайных погрешностей

При проведении расчетов считаем погрешностью Δx_i величины x_i её отклонение от среднего значения . Таким образом, в дальнейшем будем полагать, что возможные для величины x_i погрешности будут +Δx_i и -Δx_i, а диапазон изменения погрешности равен 2Δx_i.

Это условие учитывается во всех расчетах, так например, если в расчете участвуют величины диаметров валов d₀ = 12- 0,07, следует считать, что возможны наибольшие по абсолютной величине погрешности, т. е. отклонения от среднего размера, равные + 0,035 и - 0.035.

Согласно уравнению Δ_lim = 6σ можно считать, что при нормальном распределении с вероятностью, равной 0,9973, предельная случайная погрешность измерении Δ_lim = ±3σ≈ ±3s.

Предельная погрешность для совокупности, состоящей из среднеарифметических значений, равна Δ_lim = Δ_lim/ , где Δ_lim = ±3σ ≈±3s.

Из теории вероятностей известно, что дисперсия суммы нескольких независимых случайных величин равна сумме дисперсий этих величин, поэтому

D ( x₁ + x₂ + … + x_n ) = Dx₁ + Dx₂ + … + Dx_n

Так как D =σ², можно записать

σ( x₁ + x₂ + … + x_n) = 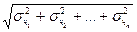или

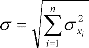(1)

Из полученного уравнения следует, что суммирование средних квадратических погрешностей для случайных величин, входящих в общую погрешность результата измерения, при их взаимной независимости и нормальном распределении производится квадратически.

2. Cуммирование систематических погрешностей.

Систематические постоянные погрешности должны входить в суммарную погрешность полностью с учетом знака, т. е. должны суммироваться алгебраически.

Систематические переменные погрешности в том случае, если определяется наибольшая величина суммарной погрешности, должны суммироваться с тем знаком, при котором абсолютная величина суммы увеличивается.

Так, например, если сумма остальных слагаемых отрицательна, то в неё следует включать наибольшее по абсолютной величине отрицательное значение систематической погрешности, если она такое значение имеет или наименьшие по абсолютной величине положительные значения, если они их принимают.

Нормирование погрешностей и формы представления результатов измерений

Основные задачи нормирования погрешностей заключаются выборе показателей, характеризующих погрешность, и установлении допускаемых значений этих показателей. Решение этих задач определяется целью измерений и использованием результатов.

Например, если результат измерения используется наряду с другими при расчете какой-то экспериментальной характеристики, то необходимо учитывать погрешности отдельных составляющих путем суммирования их СКО.

Если речь идет о контроле в пределах допуска и нет информации о законах распределения параметра и погрешности, то достаточно ограничиться доверительным интервалом с доверительна вероятностью. Эти показатели должны сопровождать результат измерений тогда, когда дальнейшая обработка результатов не предусмотрена.

Исходя из изложенного, для оценки погрешностей измерений необходимо: установить вид модели погрешности с ее характерными свойствами; определить характеристики этой модели оценить показатели точности измерений по характеристикам модели.

При установлении модели погрешности возникают типовые статистические задачи: оценка параметров закона распределения, проверка гипотез, планирование эксперимента и др.

В соответствии с МИ 1317—86 точность измерения должна выражаться одним из способов:

1) интервалом, в котором с установленной вероятностью находится суммарная погрешность измерения;

2) интервалом, в котором с установленной вероятностью находится систематическая составляющая погрешности измерений;

3) стандартной аппроксимацией функции распределения случайной составляющей погрешности измерения и средним квадратическим отклонением случайной составляющей погрешности измерения;

4) стандартными аппроксимациями функций распределения систематической и случайной составляющих погрешности измерения и их средними квадратическими отклонениями и функциями распределения систематической и случайной составляющих погрешности измерения.

В инженерной практике применяется в основном первый способ (х = a±Δ, или Δ от Δ_min до Δ_max, Р=0,9). Система допусков, например, построена на понятии предельной погрешности Δ = ±2σ при Р=0,95 (ГОСТ 8.051-81).

Числовое значение результата измерения должно заканчиваться цифрой того же разряда, что и значение погрешности Δ.

Дата добавления: 2014-09-08; просмотров: 2219; Нарушение авторских прав

Мы поможем в написании ваших работ!