Средства измерений. Виды средств измерений. Метрологические характеристики средств измерений. Классы точности средств измерений

Виды средств измерений.

Средство измерения (СИ) — это техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и/или хранящее единицу ФВ, размер которой принимается неизменным (в пределах установленной погрешности) в течение известного интервала времени.

Подметрологическими характеристиками (MX) понимают такие характеристики СИ, которые позволяют судить об их пригодности для измерений в известном диапазоне с известной точностью.

В отличие от СИ приборы или вещества, не имеющие нормированных MX, называют индикаторами.

Классификация основных СИ по РМГ 29—99.

Меры— это СИ, воспроизводящие или хранящие физическую величину заданного размера. Меры могут быть однозначными, воспроизводящими одно значение физической величины (гиря, калибр на заданный размер, образцы твердости, шероховатости, катушка сопротивления, нормальный элемент, воспроизводящий значение ЭДС), и многозначными — для воспроизведения плавно или дискретно ряда значений одной и той же физической величины (измерительный конденсатор переменной емкости, набор конечных мер, магазин емкостей, индуктивности и сопротивления, измерительные линейки).

Измерения методом сравнения с мерой выполняют с помощью специальных технических средств — компараторов (равноплечие весы, измерительный мост и т. д.). Иногда в качестве компаратора выступает человек, например при измерении длины линейкой.

Измерительные преобразователи — СИ, предназначенные для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и хранения, но не доступной для непосредственного восприятия наблюдателем. Это термопары, измерительные трансформаторы, усилители, преобразователи давления. Конструктивно они выполняются либо отдельными блоками, либо составной частью СИ.

Не следует отождествлять измерительные преобразователи с преобразовательными элементами. Последние не имеют метрологических характеристик, как, например, трансформатор тока или напряжения.

Измерительный прибор — СИ, предназначенное для переработки сигнала измерительной информации в другие, доступные для непосредственного восприятия наблюдателем формы.

Различают приборы прямого действия (амперметры, вольтметры, манометры) и приборы сравнения (компараторы).

По способу отсчета измеряемой величины СИ делятся на показывающие (аналоговые, цифровые), регистрирующие (на бумажную или магнитную ленту) и т. п.

Измерительная установка — совокупность функционально объединенных СИ и вспомогательных устройств, расположенных в одном месте. Например, поверочные установки, установки для испытания электротехнических, магнитных и других материалов.

Измерительная установка позволяет предусмотреть определенный метод измерения и заранее оценить погрешность измерения.

Измерительная система — это комплекс СИ и вспомогательных устройств с компонентами связи (проводные, телевизионные и др.), предназначенный для выработки сигналов измерительной информации в форме, удобной для автоматической обработки, передачи и/или использования в автоматических системах управления.

В отличие от измерительных установок, предусматривающих изменения режима и условий функционирования, измерительная система не воздействует на режимы работы, а предназначена только для сбора и/или хранения информации.

Частными случаями измерительной системы являются информационно-вычислительный комплекс (ИВК), информационно-измерительные системы (ИИС).

Общая структура измерительных приборов и установок

Измерения физических величин в производственной деятельности выполняются с помощью рабочих средств измерения - измерительными приборами или измерительными установками.

Измерительные приборы включают в себя: измерительный преобразователь (датчик), преобразователь сигнала в аналоговую или цифровую форму, усилитель сигнала, отсчетное устройство.

Современные приборы, кроме того, могут быть оснащены различными электронными устройствами. Например, цифровыми отсчётными устройствами, самописцами или магнитными накопителями, а также устройствами сочленения прибора с компьютером. В случае наличия у измерительных приборов цифровых выходов в виде быстродействующих портов типа USB-2 или Fire Wire (IEEE 1394) у пользователя появляются дополнительные возможности, например статистическая обработка результатов при проведении измерений в динамическом режиме, измерение параметров быстро протекающих процессов.

В зависимости от программного обеспечения процедуры измерений, появляются также многие сервисные возможности, например, компьютер, может управлять процессом измерений, проводить анализ текущей измерительной информации и т.д.

Измерительный преобразователь- это устройство, предназначенное для выработки сигнала измерительной информации в форме, удобной для её передачи, преобразования, обработки и хранения. Различают первичный, промежуточный, передающий и масштабный преобразователи.

· Первичный преобразователь занимает в измерительной цепи первое место и непосредственно воспринимает измерительную информацию.

· Промежуточный преобразователь занимает в измерительной цепи второе место.

· Передающий измерительный преобразователь предназначен для дистанционной передачи сигнала.

· Масштабный преобразователь предназначен для усиления величины в заданное число раз.

Первичный преобразователь (датчик) имеет чувствительный элемент (контактный или бесконтактный), находящийся под непосредственным воздействием измеряемой величины. Преобразователи разнообразны по конструкции и принципу действия. Они могут быть: механические, оптические, емкостные, индуктивные, лазерные и др.

Усилители могут выполняться в виде катодных повторителей, амплитудно-частотных преобразователей, согласующих устройств с выходом на компьютер и др.

Кроме измерительных приборов и вспомогательных устройств в состав измерительных установок могут входить меры или наборы мер. Например, наборы сменных шкал, объективов с разным фокусным расстоянием, наборы гирь, магазины сопротивлений и индуктивностей, нормальные гальванические элементы и т. д.

Метрологические характеристики средств измерений

Для оценки пригодности СИ к измерениям в известном диапазоне с известной точностью вводят MX СИ с целью:

· обеспечения возможности установления точности измерений;

· достижения взаимозаменяемости СИ, сравнения СИ между собой и выбора нужных СИ по точности и другим характеристикам;

· определения погрешностей измерительных систем и установок на основе MX входящих в них СИ;

· оценки технического состояния СИ при поверке.

По ГОСТ 8.009—84 устанавливают перечень MX, способы их нормирования и формы представления.

Нормальные метрологические характеристики (НМХ) устанавливаются документами. MX, определенные документами, считаются действительными. На практике наиболее распространены следующие MX СИ.

Диапазон измерений — область значений измеряемой величины, для которой нормированы допускаемые пределы погрешности СИ (для преобразователей — это диапазон преобразования).

Предел измерения — наибольшее или наименьшее значение диапазона измерения. Для мер — это номинальное значение воспроизводимой величины.

Например, у шкалы на рис. 3.2 начальный участок (~20%) сжат, потому производить отсчеты на нем неудобно. Тогда предел измерения по шкале составляет 50 ед., а диапазон — 10...50 ед.

Цена деления шкалы— разность значений величин, соответствующих двум соседним отметкам шкалы. Приборы с равномерной шкалой имеют постоянную цену деления, а с неравномерной — переменную. В этом случае нормируется минимальная цена деления.

Чувствительность — отношение изменения сигнала Δу на выходе СИ к вызвавшему это изменение изменению Δх сигнала на входе

S=Δу/ Δх

Например, для стрелочного СИ — это отношение перемещения dl конца стрелки к вызвавшему его изменению dx измеряемой величины

S=dl/ dх

Для равномерных шкал

S=const=l/x_n,

где x_n - диапазон измерений.

Чувствительность нельзя отождествлять с порогом чувствительности — наименьшим значением измеряемой величины, вызывающим заметное изменение показаний прибора.

Величину, обратную чувствительности, называют постоянной прибора

С = 1/S.

Как правило, выходным сигналом СИ является отсчет (показание) в единицах величины. В этом случае постоянная прибора С равна цене деления.

Вариация (гистерезис) — разность между показаниями СИ в данной точке диапазона измерения при возрастании и убывании измерений величины и неизменных внешних условиях:

Н= |х_в – x_у|

где х_в, х_у — значения измерений образцовыми СИ при возрастании и убывании величины х.

Следует иметь в виду, что, хотя вариация показаний СИ вызывается случайными факторами, сама она — не случайная величина.

Градуировочная характеристика - зависимость между выходным и входным сигналом СИ, полученная экспериментально. Она может быть представлена аналитически, графически или в виде таблицы.

Градуировочная характеристика может изменяться под воздействием внешних и внутренних причин. Например, при быстром изменении тока подвижная часть СИ, вследствие инерции, не успевает "следить" за изменением тока. Градуировочная характеристика в этом случае должна выражаться дифференциальным уравнением.

Основная MX СИ — погрешность СИ — есть разность между показаниями СИ и истинными (действительными) значениями ФВ.

Все погрешности СИ в зависимости от внешних условий делятся на основные и дополнительные.

Основная погрешность — это погрешность СИ при нормальных условиях эксплуатации. Как правило, нормальными условиями эксплуатации являются: температура 293±5 К или 20±5 °С, относительная влажность воздуха 65+15% при 20 °С, напряжение в сети питания 220 В+10% с частотой 50 Гц±1%, атмосферное давление от 97,4 до 104 кПа, отсутствие электрических и магнитных полей (наводок).

В рабочих условиях, зачастую отличающихся от нормальных более широким диапазоном влияющих величин, при необходимости нормируется дополнительная погрешность СИ.

Существуют три способа нормирования основной погрешности СИ:

• нормирование пределов допускаемой абсолютной (±Δ) или приведенной погрешностей, постоянных во всем диапазоне измерения;

• нормирование пределов допускаемой абсолютной (±Δ) или относительной (±δ) погрешностей в функции измеряемой величины;

• нормирование постоянных пределов допускаемой основной погрешности, различных для всего диапазона измерений одного или нескольких участков.

В качестве предела допускаемой погрешности выступает наибольшая погрешность, вызываемая изменением влияющей величины, при которой СИ по техническим требованиям может быть допущено к применению. То же самое относится и к дополнительным погрешностям.

При этом исходят из следующих положений:

1) дополнительная погрешность имеет такой же вид, что и основная (абсолютная, относительная и приведенная);

2) дополнительные погрешности, вызванные различными влияющими факторами, должны нормироваться раздельно.

В общем виде суммарная абсолютная погрешность СИ при влияющих факторах имеет вид

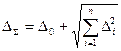
где Δ₀ — основная погрешность СИ; Δ_i — дополнительная погрешность, вызванная изменением i-го влияющего фактора.

Иногда дополнительную погрешность нормируютв виде коэффициента, указывающего, на сколько или во сколько раз изменяется погрешность при отклонении номинального значения. Например, указание, что температурная погрешность вольтметра составляет ±1% на 10 °С, означает, что при изменении среды на каждые 10 ⁰С добавляется дополнительная погрешность 1%.

Вследствие сложности разделения дополнительных и основных погрешностей поверку СИ выполняют только при нормальных условиях (т. е. дополнительные погрешности исключены).

В соответствии с ГОСТ 8.401—80 для пределов допускаемой основной (и дополнительной) погрешностей предусмотрены различные способы выражения в виде абсолютной, относительной и приведенной погрешности.

Абсолютная погрешность — разность между показанием х СИ и действительным значением ха измеряемой величины

Δ =|x – x_д|

где в качестве х_д выступает либо номинальное значение (например, меры), либо значение величины, измеренной более точным (не менее чем на порядок, в 10 раз) СИ.

Абсолютная погрешность выражается в единицах измеряемой физической величины и может быть задана:

а) либо одним числом: Δ = ±а;

б) либо в виде линейной зависимости: Δ = ±bх; Δ=±(а+bx);

в) в виде функции Δ =f(х) или графика, таблицы.

Относительная погрешность.Поскольку абсолютная погрешность выражается в абсолютных единицах физической величины, то это не дает возможность сравнить СИ и измеряющие разные физические величины. Для этой цели можно использовать относительные погрешности, как отношение абсолютной погрешности к действительному х_д (x_d) значению, выраженные в процентах

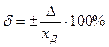
Эта формула показывает, что для одного и того же СИ δ уменьшается с ростом х_д и приближается к ∞ при х_д→0. То есть при измерении на начальном участке шкалы с начальной нулевой отметкой погрешности измерения могут быть сколь угодно велики. Поэтому в метрологии существует принцип запрета измерений на таких участках шкалы СИ.

Приведенная погрешность.Указание только абсолютной погрешности не позволяет сравнивать между собой по точности СИ с разным пределом измерений, а указание относительной погрешности также ограничено из-за непостоянства величины δ.

Поэтому получило большое распространение нормирование приведенной погрешности как отношение Δ к нормируемому значению x_N (в %):

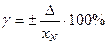
Нормирующее значение x_N выбирают в зависимости от вида и характера шкалы прибора.

Различают равномерные и неравномерные шкалы. Последние делятся на существенно неравномерные и степенные.

Под существенно неравномерной шкалой понимают шкалу с сужающимися делениями, на которой отметка, соответствующая полусумме начального и конечного значения рабочей части шкалы, расположена между 65 и 100% длины этой рабочей части.

Под степенной шкалой понимают шкалу с расширяющимися или сужающимися делениями, но не попадающими под определение существенно неравномерных.

Тогда нормирующее значение x_N принимается равным:

• конечному значению рабочей части шкалы x_N= х_к если нулевая отметка — на краю или вне рабочей части шкалы

• сумме конечных значений шкалы (без учета знака), если нулевая отметка — внутри шкалы (x_N = 20+20 = 40; x_N= 20+40 = 60);

• длине шкалы, если она существенно неравномерна. В этом случае, поскольку длина выражается в миллиметрах, то абсолютную погрешность надо выражать также в миллиметрах;

• номинальному значению х, если СИ предназначено для измерения отклонения измеряемой величины от номинального значения.

Специфическим видом погрешности цифровых СИ и дискретных преобразователей является погрешность квантования, которая вносится округлением значения измеряемой величины и номинального значения.

Поскольку измеряемая величина х может принимать случайные значения в интервале от +Δ до -Δ, то погрешность квантования есть случайная аддитивная статическая погрешность. Она не зависит ни от текущего значения х, ни от скорости изменения х во времени.

Погрешность от вариации (гистерезиса) Δ_H нормируется установлением предела H_p без учета знака допускаемой вариации выходного сигнала (показания) СИ.

Характеристику погрешности СИ, в том числе и в заданном интервале, нормируют установлением предела (положительного и отрицательного) Δ допускаемой погрешности совместно с Н_р.

Классы точности средств измерений.

Приведенная в предыдущем параграфе номенклатура MX в местном смысле предполагает строгое нормирование MX СИ, используемых при высокоточных лабораторных измерениях и метрологической аттестации других СИ.

При технических измерениях, когда не предусмотрено выделение случайных и систематических составляющих, когда не существенна динамическая погрешность СИ, когда не учитываются влияющие (дестабилизирующие) факторы и т.д., можно пользоваться более грубым нормированием — присвоением СИ определенного класса точности по ГОСТ 8.401—80.

Класс точности — это обобщенная MX, определяющая различные свойства СИ. Например, у показывающих электроизмерительных приборов класс точности помимо основной погрешности включает также вариацию показаний, а у мер электрических величин — величину нестабильности (процентное изменение значения меры в течение года). Класс точности СИ уже включает систематическую и случайную погрешности. Однако он не является непосредственной характеристикой точности измерений, выполняемых с помощью этих СИ, поскольку точность измерения зависит и от метода измерения, взаимодействия СИ с объектом, условий измерения и т.д.

В частности, чтобы измерить величину с точностью до 1%, недостаточно выбрать СИ с погрешностью 1%. Выбранное СИ должно обладать гораздо меньшей погрешностью, так как нужно учесть как минимум еще погрешность метода.

В связи с большим разнообразием как самих СИ, так и их MX, ГОСТ 8.401—80 устанавливает несколько способов назначения классов точности. При этом в основу заложены следующие положения:

• в качестве норм служат пределы допускаемых погрешностей, включающие систематические и случайные составляющие;
• основная δ_осн и все виды дополнительных погрешностей δ_доп нормируются порознь.

Определяя класс точности, нормируют прежде всего пределы допускаемой основной погрешности δ_осн. Пределы допускаемой дополнительной погрешности устанавливают в виде дольного (кратного) значения [δ_осн].

Классы точности присваивают СИ при их разработке по результатам государственных приемочных испытаний. Если СИ предназначены для измерения одной и той же физической величины, но в разных диапазонах, или — для измерения разных физических величин, то этим СИ могут присваиваться разные классы точности как по диапазонам, так и по измеряемым физическим величинам.

В эксплуатации СИ должны соответствовать этим классам точности. Однако при наличии соответствующих эксплуатационных требований класс точности, присвоенный на производстве, в эксплуатации может понижаться.

ГОСТ 8.401—80 в качестве основных устанавливает три вида классов точности СИ:

• для пределов допускаемой абсолютной погрешности в единицах измеряемой величины или делениях шкалы;

• для пределов допускаемой относительной погрешности в виде ряда чисел

δ = ±А·10ⁿ

где А= 1; 1.5; (1.6); 2; 2.5; (3); 4; 5 и 6; значения 1.6 и 3 —допускаемые, но не рекомендуемые; n= 1; 0; -1; -2;...;

• для пределов допускаемой приведенной погрешности с тем же рядом А: γ = ±А·10ⁿ.

Классы точности СИ, выраженные через абсолютные погрешности, обозначают прописными буквами латинского алфавита или римскими цифрами. При этом чем дальше буква от начала алфавита, тем больше значения допускаемой абсолютной погрешности. Например, СИ класса С более точен, чем СИ класса М, т. е. это число — условное обозначение и не определяет значение погрешности.

Класс точности через относительную погрешность СИ назначается двумя способами.

1. Если погрешность СИ имеет в основном мультипликативную составляющую, то пределы допускаемой основной относительной погрешности устанавливают по формуле

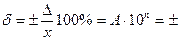q

Так обозначают классы точности мостов переменного тока, счетчиков электроэнергии, делителей напряжения, измерительных трансформаторов и др.

1. Если СИ имеют как мультипликативную, так и аддитивную составляющие, то класс точности обозначается двумя цифрами, соответствующими значениям c и d формулы:

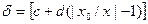
Здесь с и d выражаются также через ряд A. Причем, как правило, c>d. Например, класс точности 0,02/0,01 означает, что с=0,02, а d=0,01, т. е. приведенное значение относительной погрешности к началу диапазона измерения γ_н = 0,02%, а к концу — γ_к= 0,01%.

Кроме того, ГОСТ 22261—94 устанавливает пределы допускаемой основной погрешности в виде относительной погрешности, выраженной в децибелах (дБ):

δ = Aʹ·lg(l + Δ/x),

где А'= 10 при измерении энергетических величин (мощности, энергии, плотности энергии); А'= 20 при измерении силовых электромагнитных величин (напряжения, силы тока, напряженности поля).

Следует иметь в виду, что если два прибора имеют разные чувствительности

S₁=-100дБ/Вт и S₂=-95 дБ/Вт, то значение чувствительности у второго СИ выше, чем у первого, так как -95> -100.

Наиболее широкое распространение (особенно для аналоговых СИ) получило нормирование класса точности по приведенной погрешности:

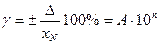
Условное обозначение класса точности в этом случае зависит от нормирующего значения х_N, т. е. от шкалы СИ.

Если x_N представляется в единицах измеряемой величины, то класс точности обозначается числом, совпадающим с пределом допускаемой приведенной погрешности. Например, класс 1,5 означает, что γ = 1,5%.

Если x_N — длина шкалы (например, у амперметров), то класс 1.5 означает, что γ =1,5% длины шкалы.

Сравнения способов выражения погрешностей позволяет высказать некоторые соображения.

При известном классе точности СИ, выраженном через приведенную погрешность γ и чувствительность S (отношение длины шкалы прибора к его диапазону измерения) абсолютная погрешность СИ составит

Δ=γx_N/100S, (1)

а относительная на отметке х, соответственно,

δ= γx_N/xS. (2)

При форме записи 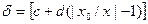абсолютная погрешность имеет вид:

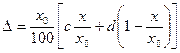(3)

Расчетные коэффициенты с и d округляются до принятых рядом А, а соотношение их с классом точности по приведенной погрешности γ

приведено в следующей таблице:

Таблица соотношения классов точности γ и коэффициентов c/d

Таблица формул вычисления погрешностей и обозначение классов точности СИ

Вид погрешности	Формула по тексту	Примеры пределов допускаемой погрешности	Обозначение класса точности	СИ, реко-мендуемые к обозначению таким способом
В НТД	На СИ
Абсолютная	Δ=±a Δ=±(a+bx)	Δ=±0.2 А	Класс точности N или класс точности III	N   III	меры
Относительная		δ=±0.5%	Класс точности 0.5	0.5 в круге	Мосты, счетчики, делители, трансформаторы
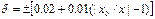
		Класс точности 0.02/0.01	0.02/0.01	Цифровые СИ, магазины емкостей
Приведенная		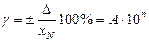при xN=xк γ=±1.5%	Класс точности 1.5	1.5	Аналоговые СИ, если xN – в единицах величины
при xN, равному длине шкалы, мм γ=±0.5%	Класс точности 0.5	0.5 с галочкой под цифрой	Омметры, если xN определяется длиной шкалы

Из формулы относительной погрешности δ=Δ/х видно, что ее значение растет обратно пропорционально х и изменяется по гиперболе, т. е. относительная погрешность равна классу СИ δ₀ лишь на последней отметке шкалы (х = x_к. При х→0 величина δ→∞. При уменьшении измеряемой величины до значения x_min относительная погрешность достигает 100%. Такое значение измеряемой величины называется порогом чувствительности.

Резюмируя изложенное, следует сказать, что если класс точности СИ установлен по наибольшему допускаемому приведенному значению погрешности а для оценки погрешности конкретного измерения необходимо знать значение абсолютной или относительной погрешности в данной точке, то в этом случае выбор СИ, например, класс 1 (γ = 1%) для измерения с относительной погрешностью ±1% будет правильным, если верхний предел x_N СИ равен измеряемому значению х величины. В остальных случаях относительную погрешность измерения необходимо определять по формуле

(4)

Пример.Отсчет по шкале прибора с пределами измерений 0 — 50 А и равномерной шкалой составил 25А. Пренебрегая другими видами погрешностей измерения, оценить пределы допускаемой абсолютной погрешности этого отсчета при использовании различных СИ класса точности: 0,02/0,01; (0.5 в кружочке) и 0,5.

Решение.

1. Для СИ класса точности 0,02/0,01 имеем:

,

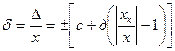так как х = 25; х_к = 50; с =0,02; d = 0,01 и δ - в %,

то

Δ = ±[0.02 + 0.01(50/25-1) 25 0.01] = ±0,008А.

1. Для СИ класса точности (0.5) (в кружочке):

δ = ±Δ/х·100% ;

Δ = ±0,01·25·0,5 =±0,185 А.

1. Для СИ класса точности 0,5:

γ = ±Δ/х_N·100%,где х_N=50,

тогда

Δ = ±0,01·50·0,05 = ±0,25 А.

Выбор средств измерений

Дата добавления: 2014-09-08; просмотров: 1662; Нарушение авторских прав

Мы поможем в написании ваших работ!