Порталы:

Биология Война География Информатика Искусство История Культура Лингвистика Математика Медицина Охрана труда Политика Право Психология Религия Техника Физика Философия Экономика

Мы поможем в написании ваших работ!

Метрология, ее задачи и структура. Законодательная база метрологии. Физические величины и шкалы. Международная система единиц СИ

Читайте также:

Метрология, ее задачи и структура.

С 1 января 2001 г. на территории России и стран СНГ взамен ГОСТ 16263-70 вводятся рекомендации РМГ 29-99, содержащие основные термины и определения в области метрологии, согласованные с международными стандартами ИСО 31(0-13) и ИСО 1000, регламентирующими использование дольных, кратных и других единиц при измерениях.

В соответствии с этими документами метрология — это наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.

Таким образом, метрология включает три взаимосвязанные проблемы: реализация процессов измерения; обеспечение их единства; методы и средства измерений.

Основными задачами метрологии согласно РМГ 29-99 являются:

· установление единиц физических величин;

· установление государственных эталонов и образцовых средств измерений;

· разработка методов передачи размеров единиц от эталонов или образцовых средств измерений рабочим средствам измерений.

· разработка теории, методов и средств измерения и контроля;

· обеспечение единства измерений;

· разработка методов оценки погрешностей, состояния средств измерения и контроля;

В зависимости от цели различают три раздела метрологии: теоретический, законодательный и прикладной.

В теоретической (фундаментальной) метрологии разрабатываются фундаментальные основы этой науки.

Предметом законодательной метрологии является установление обязательных технических и юридических требований по применению единиц физических величин, эталонов, методов и средств измерений, направленных на обеспечение единства и необходимой точности измерений.

Практическая (прикладная) метрология освещает вопросы практического применения разработок теоретической и положений законодательной метрологии.

Законодательная база метрологиивключает следующие основные документы:

· Закон РФ "Об обеспечении единства измерений" от 27.04.93 № 4871-1 в редакции 2003г.;

· РМГ 29-99. "Государственная система обеспечения единства измерений. Метрология. Основные термины и определения";

· МИ 2247-93 ГСИ." Метрология. Основные термины и определения" (МИ – рекомендации государственных научных центров);

· ГОСТ 8.417-2002 "ГСИ. Единицы физических величин";

· ПР 50.2.006-94 "ГСИ. Поверка средств измерений. Организация и порядок проведения";

· ПР 50.2.009-94 "ГСИ. Порядок проведения испытаний и утверждения типа средств измерения";

· ПР 50.2.014-94 "ГСИ. Аккредитация метрологических служб юридических лиц на право поверки средств измерений";

· МИ 2277-94 "ГСИ. Система сертификации средств измерений. Основные положения и порядок проведения работ";

· ПР 50.2.002-94 "ГСИ. Порядок осуществления государственного метрологического надзора за выпуском, состоянием и применением средств измерений, аттестованными методиками выполнения измерений, эталонами и соблюдением метрологических правил и норм";

· ПР 50.2.004-94 «ГСИ. Порядок осуществления государственного метрологического надзора количеством фасованных товаров в упаковках любого вида при их расфасовке и продаже»;

· ПР 50.2.017-95 «ГСИ. Положение о российской системе калибровки»;

· Постановление Госстандарта России от 08.02.1994г. № 8 «Порядок лицензирования деятельности по изготовлению, ремонту, продаже и прокату средств измерений»;

· Постановление Госстандарта России от 08.02.1994г. № 8 «Порядок осуществления государственного метрологического надзора за количеством товаров, отчуждаемых при совершении торговых операций»;

· Постановление Госстандарта России от 28.12.1995г. № 95 «Порядок аккредитации метрологических служб юридических лиц на право проведения калибровочных работ»;

· Постановление Госстандарта России от 08.02.1994г. № 8 «Требования к государственным центрам испытаний средств измерений и порядок их аккредитации»;

· ИСО 10012-1:1992 «Требования, гарантирующие качество измерительного оборудования. – Часть 1. Система подтверждения метрологической пригодности измерительного оборудования».

Закон "Об обеспечении единства измерений" осуществляет регулирование отношений, связанных с обеспечением единства измерений в Российской Федерации, в соответствии с Конституцией РФ.

В сферах, которые напрямую не контролируются государственными органами, действует Российская система калибровки, также направленная на обеспечение единства измерений. Система калибровки - совокупность субъектов деятельности и калибровочных работ, направленных на обеспечение единства измерений в сферах, не подлежащих государственному метрологическому контролю и надзору и действующих на основе установленных требований к организации и проведению калибровочных работ.

Физические величины (ФВ) и шкалы.

Все объекты окружающего мира характеризуются своими свойствами. Свойство — категория качественная. Для количественного описания различных свойств процессов и физических тел вводится понятие величины. Величина — это свойство чего-либо, что может быть выделено среди других свойств и оценено тем или иным способом, в том числе и количественно.

Таким образом, физические величины — это измеренные свойства физических объектов и процессов, с помощью которых они могут быть изучены.

Физические величины целесообразно разделить на измеряемые и оцениваемые. Измеряемые ФВ могут быть выражены количественно в виде определенного числа установленных единиц измерения, возможность введения и использования последних является важным отличительным признаком измеряемых ФВ. Физические величины, для которых по тем или иным причинам не может быть введена единица измерения, могут быть только оценены.

По видам явлений ФВ делятся на следующие группы:

• вещественные, т.е. описывающие физические и физико-химические свойства веществ, материалов и изделий из них. К этой группе относятся масса, плотность, электрическое сопротивление, емкость, индуктивность и др. Иногда указанные ФВ называют пассивными. Для их измерения необходимо использовать вспомогательный источник энергии, с помощью которого формируется сигнал измерительной информации. При этом пассивные ФВ преобразуются в активные, которые и измеряются;

• энергетические, т.е. величины, описывающие энергетические характеристики процессов преобразования, передачи и использования энергии. К ним относятся ток, напряжение, мощность, энергия. Эти величины называют активными. Они могут быть преобразованы в сигналы измерительной информации без использования вспомогательных источников энергии;

• характеризующие протекание процессов во времени. К этой группе относятся различного рода спектральные характеристики, корреляционные функции и др.

По принадлежности к различным группам физических процессов ФВ делятся на

пространственно-временные,

механические,

тепловые,

электрические и магнитные,

акустические,

световые,

физико-химические,

ионизирующих излучений,

атомной и ядерной физики.

По степени условной независимости от других величин данной группы ФВ делятся на

основные (условно независимые),

производные (условно зависимые),

дополнительные.

По наличию размерности ФВ делятся на размерные, т. е. имеющие размерность, и безразмерные.

Единица физической величины [Q] — это ФВ фиксированного размера, которой условно присвоено числовое значение, равное единице и применяемое для количественного выражения однородных ФВ. Значение физической величины Q — это оценка ее размера в виде некоторого числа принятых для нее единиц.

Шкалы физических величин.

Величины оценивают при помощи шкал. Шкала величины — упорядоченная последовательность ее значений, принятая по соглашению на основании результатов точных измерений.

Шкала физической величины — это упорядоченная последовательность значений ФВ, принятая по соглашению на основании результатов точных измерений. Термины и определения теории шкал измерений изложены в документе МИ 2365-96.

В соответствии с логической структурой проявления свойств различают пять основных типов шкал измерений.

1. Шкалы наименований (шкалы классификации). Такие шкалы используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности. Эти свойства нельзя считать физическими величинами, поэтому шкалы такого вида не являются шкалами ФВ. Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен.

Примером шкал наименований являются широко распространенные атласы цветов, предназначенные для идентификации цвета.

2. Шкалы порядка (шкалы рангов). Если свойство данного эмпирического объекта проявляет себя в отношении эквивалентности и порядка по возрастанию или убыванию количественного проявления свойства, то для него может быть построена шкала порядка. Она является монотонно возрастающей или убывающей и позволяет установить отношение больше/меньше между величинами, характеризующими указанное свойство. В шкалах порядка принципиально нельзя ввести единицы измерения, так как для них не установлено отношение пропорциональности и соответственно нет возможности судить, во сколько раз больше или меньше конкретные проявления свойства.

Условная шкала — это шкала порядка ФВ, исходные значения которой выражены в условных единицах. Например, шкала вязкости Энглера, 12-балльная шкала Бофорта для измерения силы морского ветра.

Широкое распространение получили шкалы порядка с нанесенными на них реперными точками. К таким шкалам, например, относится шкала Мооса для определения твердости минералов, которая содержит 10 опорных (реперных) минералов с различными условными числами твердости: тальк — 1; гипс — 2; кальций — 3; флюорит — 4; апатит —■ 5; ортоклаз — 6; кварц — 7; топаз — 8; корунд — 9; алмаз — 10. Отнесение минерала к той или иной градации твердости осуществляется на основании эксперимента, который состоит в том, что испытуемый материал царапается опорным. Если после царапанья испытуемого минерала кварцем G) на нем остается след, а после ортоклаза F) — не остается, то твердость Испытуемого материала составляет более 6, но менее 7. Более точного ответа в этом случае дать невозможно.

Определение значения величин при помощи шкал порядка нельзя считать измерением, так как на этих шкалах не могут быть введены единицы измерения. Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным.

3. Шкалы интервалов (шкалы разностей). Эти шкалы являются дальнейшим развитием шкал порядка и применяются для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало — нулевую точку. К таким шкалам относится летосчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо Рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов.

На шкале интервалов определены действия сложения и вычитания интервалов. Действительно, по шкале времени интервалы можно суммировать или вычитать и сравнивать, во сколько раз один интервал больше другого, но складывать даты каких-либо событий бессмысленно.

Шкала интервалов величины Q можно представить в виде Q =Q₀ + q[Q], где q — числовое значение величины; Q₀— начало отсчета шкалы; [Q] — единица рассматриваемой величины. Такая шкала полностью определяется заданием начала отсчета Q₀ шкалы и единицы данной величины [Q]. Задать шкалу можно двумя путями. При первом пути выбираются два значения Q₀ и Q_l величины, которые относительно просто реализованы физически. Эти значения называются опорными точками, или основными реперами, а интервал (Q₁ — Q₀) — основным интервалом. Точка Q₀ принимается за начало отсчета, а величина (Q₁ — Q₀)/n = [Q] за единицу Q. При этом число единиц n выбирается таким, чтобы [Q] было целой величиной. Перевод одной шкалы интервалов Q = Q_0l + q_l[Q]_l в другую Q=Q₀₂ + q₂[Q]₂ осуществляется по формуле

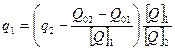(1.1)

При втором пути единица воспроизводится непосредственно как интервал, его некоторая доля или некоторое число интервалов размеров данной величины, а начало отсчета выбирается каждый раз по-разному в зависимости от конкретных условий изучаемого явления. Пример такого подхода — шкала времени, в которой 1 с = 9 192 631 770 периодов излучения, соответствующих переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. За начало отсчета принимается начало изучаемого явления.

4. Шкалы отношений. Эти шкалы описывают свойства эмпирических объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода — аддитивные), а в ряде случаев и пропорциональности (шкалы первого рода — пропорциональные). Их примерами являются шкалы массы (второго рода) и термодинамической температуры (первого рода).

В шкалах отношений существует однозначный естественный критерий нулевого количественного проявления свойства и единица измерений. С формальной точки зрения шкала отношений является шкалой интервалов с естественным началом отсчета. К значениям, полученным по этой шкале, применимы все арифметические действия, что имеет важное значение при измерении ФВ. Шкалы отношений — самые совершенные. Они описываются уравнением Q=q[Q], где Q — ФВ, для которой строится шкала; [Q] — ее единица измерения; q — числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением q₂ = q_l [Q₁]/ [Q₂].

5. Абсолютные шкалы. Под абсолютными понимают шкалы, обладающие всеми признаками шкал отношений, но дополнительно имеющие естественное однозначное определение единицы измерения и не зависящие от принятой системы единиц измерения. Такие шкалы соответствуют относительным величинам: коэффициенту усиления, ослабления и др. Для образования многих производных единиц в системе СИ используются безразмерные и счетные единицы абсолютных шкал.

Пример для практического занятия.

Пример 1.1. Шкала Фаренгейта является шкалой интервалов. На ней Q₀ — температура смеси льда, поваренной соли и нашатыря, Q₁ — температура человеческого тела. Единица измерения — градус Фаренгейта: 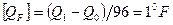. Температура таяния смеси льда, соли и нашатыря оказалась равной 32°F, а температура кипения воды — 212°F. По шкале Цельсия Q₀ — температура таяния льда, Q₁ — температура кипения воды. Градус Цельсия .

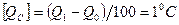Требуется получить формулу для перехода от одной шкалы к другой.

Решение. Формула для перехода определяется в соответствии с выражением (1.1). Значение разности температур по шкале Фаренгейта между точкой кипения воды и точкой таяния льда составляет 212°F - 32°F = 180°F. По шкале Цельсия интервал температур равен 100°С. Следовательно, 100°С = 180°F и отношение размеров единиц

Числовое значение интервала между началами отсчета по рассматриваемым шкалам, измеренного в градусах Фаренгейта ([Q]_l = F), равно 32. Переход от температуры по шкале Фаренгейта к температуре по шкале Цельсия производится по формуле

Системы физических величин и их единиц, система СИ.

Размер физической величины — это количественное содержание в данном объекте свойства, соответствующего понятию "физическая величина". Например, каждое тело обладает определенной массой, вследствие чего тела можно различать по их массе, т.е. по размеру интересующей нас ФВ.

Значение физической величины получают в результате ее измерения или вычисления в соответствии с основным уравнением измерения Q=q[Q], связывающим между собой значение ФВ Q, числовое значение q и выбранную для измерения единицу [Q]. В зависимости от размера единицы будет меняться числовое значение ФВ, тогда как размер ее будет оставаться неизменным.

Размерность единиц ФВ - dim Q — выражение в форме степенного многочлена, отражающее связь данной величины с основными ФВ. Коэффициент пропорциональности принят равным единице:

dim Q = L^αM^βT^γI^δ..,

где L, М, Т, I— условные обозначения основных величин данной системы; α, β, γ, δ — целые или дробные, положительные или отрицательные вещественные числа. Показатель степени, в которую возведена размерность основной величины, называют показателем размерности. Если все показатели размерности равны нулю, то такую величину называют безразмерной.

Над размерностями можно производить действия умножения, деления, возведения в степень и извлечение корня. Понятие размерности широко используется:

• для перевода единиц из одной системы в другую;

• для проверки правильности сложных расчетных формул, полученных в результате теоретического вывода;

• при выяснении зависимости между величинами;

• в теории физического подобия.

Совокупность ФВ, образованная в соответствии с принятыми принципами, когда одни величины принимаются за независимые, а другие являются их функциями, называется системой физических величин.

Обоснованно, но произвольным образом выбираются несколько ФВ, называемых основными. Остальные величины, называемые производными, выражаются через основные на основе известных уравнений связи между ними. Примерами производных величин могут служить: плотность вещества, определяемая как масса вещества, заключенного в единице объема; ускорение — изменение скорости за единицу времени и др.

Согласованная Международная система единиц физических величин была принята в 1960 г. XI Генеральной конференцией по мерам весам. Международная система - СИ (SI), SI - начальные буквы французского наименования Systeme International.

В Российской Федерации система СИ введена ГОСТ 8.417—81.

В названии системы ФВ применяют символы величин, принятых за основные. Например, система величин механики, в которой в качестве основных используются длина (L), масса (М) и время (T), называется системой LMT. Действующая в настоящее время международная система СИ должна обозначаться символами LMTIQNJ, соответствующими символам основных величин: длине (L), массе (М), времени (Т), силе электрического тока (I), температуре (Q), количеству вещества (N) и силе света (J) (таблица 1.1).

· Метр равен длине пути, проходимого светом в вакууме за 1/299.792.458 долю секунды.

· Килограмм равен массе международного прототипа килограмма.

· Секунда равна 9.192.631.770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.

· Ампер равен силе не изменяющегося во времени электрического тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызывает на каждом участке проводника длиной 1 м силу взаимодействия, равную 2•10 в минус 7-ой степени Н.

· Кельвин равен 1/273,16 части термодинамической температуры тройной точки воды.

· Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 0.012 кг.

· Кандела равна силе света в заданном направлении источника, испускающего монохроматическое излучение частотой 540•10 в 12-ой степени Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср.

· Радианравен углу между двумя радиусами окружности, дуга между которыми по длине равна радиусу.

· Стерадианравен телесному углу с вершиной в центре сферы, вырезающему на поверхности сферы площадь, равную площади квадрата со стороной, по длине равной радиусу сферы.

Производные единицы системы СИ, имеющие собственное название, приведены в табл. 1.2.

Таблица 1.1. Основные и дополнительные единицы системы СИ.

Величина	Единица
Наименование	Размерность	Рекомендуемое обозначение	Наименование	Обозначение
русское	междуна- родное
Основные
Длина	L	l	метр	м	m
Масса	M	m	килограмм	кг	kg
Время	T	t	секунда	с	s
Сила электри- ческого тока	I	I	ампер	А	A
Теромодина- мическая температура	Q	T	кельвин	К	K
Количество вещества	N	n, v	моль	моль	mol
Сила света	J	J	канделла	кд	cd
Дополнительные
Плоский угол	-	-	радиан	рад	rad
Телесный угол	-	-	стерадиан	ср	sr

Таблица 1.2. Производные единицы системы СИ, имеющие специальное название.

Величина	Единица
Наименование	Размер-ность	Наимено-вание	Обозна-чение	Выражение через единицы Си
Частота	Т^-1	герц	Гц	с^-1
Сила, вес	LMT^-2	ньютон	Н	м∙кг∙с^-2
Давление, механическое напряжение	L^-1MT^-2	паскаль	Па	м^-1∙кг∙с^-2
Энергия, работа, количество теплоты	L²MT^-2	джоуль	Дж	м²∙кг∙с^-2
Мощность	L²MT^-3	ватт	Вт	м²∙кг∙с^-3
Количество электричества	TI	кулон	Кл	с∙А
Электрический напряжение, потенциал, электродвижущая сила	L²MT^-3I^-1	вольт	В	м²∙кг∙с^-3∙А^-1
Электрическая емкость	L^-2M^-1T⁴I²	фарад	Ф	м^-2∙кг^-1∙с⁴∙А²
Электрическое сопротивление	L²MT^-3I^-2	ом	Ом	м²∙кг∙с^-3∙А^-2
Электрическая проводимость	L^-2M^-1T³I²	сименс	См	м^-2∙кг^-1∙с³∙А²
Поток магнитной индукции	L²MT^-2I^-1	вебер	Вб	м²∙кг∙с^-2∙А^-1
Магнитная индукция	MT^-2I^-1	тесла	Тл	кг∙с^-2∙А^-1
Индуктивность	L²MT^-2I^-2	генри	Гн	м²∙кг∙с^-2∙А^-2
Световой поток	J	люмен	лм	кд∙ср
Освещенность	L^-2J	люкс	лк	м^-2∙кд∙ср
Активность радионуклида	Т^-1	беккерель	Бк	с^-1
Поглощенная доза ионизирующего излучения	L²T^-2	грей	Гр	м²∙с^-2
Эквивалентная доза излучения	L²T^-2	зиверт	Зв	м²∙с^-2

Производные единицы бывают когерентными и некогерентными. Когерентной называется производная единица ФВ, связанная с другими единицами системы уравнением, в котором числовой множитель принят равным единице. Например, единицу скорости образуют с помощью уравнения, определяющего скорость прямолинейного и равномерного движения точки: v = L/t, где L — Длина пройденного пути; t — время движения. Подстановка вместо L и t их единиц в системе СИ дает v = 1 м/с. Следовательно, единица скорости является когерентной.

Единицы ФВ делятся на системные и внесистемные.

Системная единица — единица ФВ, входящая в одну из принятых систем. Все основные, производные, кратные и дольные единицы являются системными.

Внесистемная единица — это единица ФВ, не входящая ни в одну из принятых систем единиц. Внесистемные единицы по отношению к единицам СИ разделяют на четыре вида:

•-допускаемые наравне с единицами СИ, например: единицы массы — тонна; плоского угла — градус, минута, секунда; объема — литр и др. Внесистемные единицы, допускаемые к применению наравне с единицами СИ, приведены в табл. 1.3;

• допускаемые к применению в специальных областях, например: астрономическая единица, парсек, световой год — единицы длины в астрономии; диоптрия — единица оптической силы в оптике; электрон-вольт — единица энергии в физике и т.д.;

• временно допускаемые к применению наравне с единицами СИ, например: морская миля — в морской навигации; карат — единица массы в ювелирном деле и др. Эти единицы должны изыматься из употребления в соответствии с международными соглашениями;

• изъятые из употребления, например: миллиметр ртутного столба — единица давления; лошадиная сила — единица мощности и некоторые другие.

Таблица 1.3. Внесистемные единицы, допускаемые к применению наравне с единицами СИ

Наименование величины	Единица
Наименование	Обозна-чение	Соотношение с единицей СИ
масса	тонна	т	10³ кг
атомная единица массы	а. е. м.	1.66057∙10^{-27 кг (приблизительно)}
время	минута	мин	60 с
час	ч	3600 с
сутки	сут	86400 с
плоский угол	градус	°	(π/180) рад=1.745329..∙10^-2 рад
минута	…′	(π/10800) рад=2.908882..∙10^-4 рад
секунда	…″	(π/648000) рад=4.848137..∙10^-6 рад
град	град	(π/200) рад
объем	литр	л	10^{-3 м3}
длина	астрономическая единица	а. е.	1.45598∙10¹¹ м (приблизительно)
световой год	св. год	9.4605∙10¹⁵ м (приблизительно)
парсек	пк	3.0857∙10¹⁶ м (приблизительно)
оптическая сила	диоптрия	дптр	1 м^-1
площадь	гектар	га	10⁴ м²
энергия	электрон-вольт	эВ	1.60219∙10^-19 Дж (приблизительно)
полная мощность	вольт-ампер	В∙А	-
реактивная мощность	вар	вар	-

Различают кратные и дольные единицы ФВ.

Кратная единица— это единица ФВ, в целое число раз превышающая системную или внесистемную единицу. Например, единица длины - километр - равна 10³ м, т.е. кратна метру.

Дольная единица — единица ФВ, значение которой в целое число раз меньше системной или внесистемной единицы. Например, единица длины - миллиметр равна 10^{-3 м, т.е. является дольной. Приставки для образования кратных и дольных единиц приведены в табл. 1.4.}

В системе СИ впервые введено понятие дополнительных единиц, к которым отнесены единицы плоского и телесного углов — радиан и стерадиан.

Таблица 1.4. Образование дольных и кратных единиц и их наименований

Множи-тель	При-ставка	Обозначение приставки	Множи-тель	При-ставка	Обозначение приставки
Между-народное	Русское	Между-народное	Русское
10¹⁸	экса	E	Э	10^-1	деци	d	д
10¹⁵	пета	P	П	10^-2	санти	c	с
10¹²	тера	T	Т	10^-3	мили	m	м
10⁹	гига	G	Г	10^-6	микро	μ	мк
10⁶	мега	M	М	10^-9	нано	n	н
10³	кило	k	к	10^-12	пико	p	п
10²	гекто	h	г	10^-15	фемто	f	ф
10¹	дека	da	да	10^-18	атто	a	а

<== предыдущая страница	\|	следующая страница ==>
ОСНОВНЫЕ ПРАВИЛА ПРОЕКТИРОВАНИЯ СТРОИТЕЛЬНОЙ ЧАСТИ ПРЕДПРИЯТИЙ ОБЩЕСТВЕННОГОПИТАНИЯ	\|	Виды и методы измерений. Качество измерений. Классификация погрешностей измерения. Расчет погрешностей измерения (начало)

Дата добавления: 2014-09-08; просмотров: 962; Нарушение авторских прав

Мы поможем в написании ваших работ!

lektsiopedia.org - Лекциопедия - 2013 год. | Страница сгенерирована за: 0.008 сек.