Состав и структура космической системы наблюдения Земли

Космическая система наблюдения Земли может являться частью более обширной системы исследования природных ресурсов (в зависимости от задач системы), включающей космические, авиационные наземные, морские системы наблюдения.

Выделение конкретной системы из внешней среды является субъективным фактором и определяется целями проектирования.

Качество решения задач определяется параметрами системы и характеристиками входящих в космическую систему компонентов.

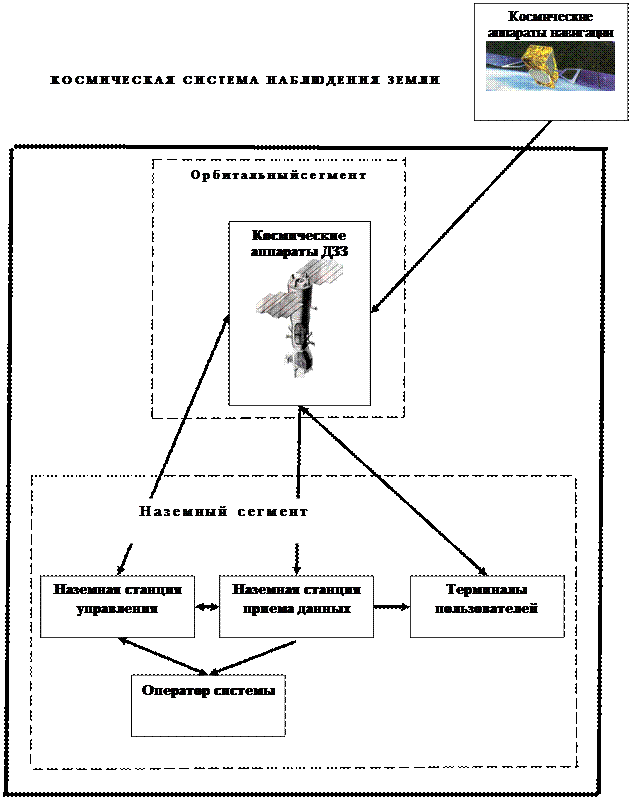
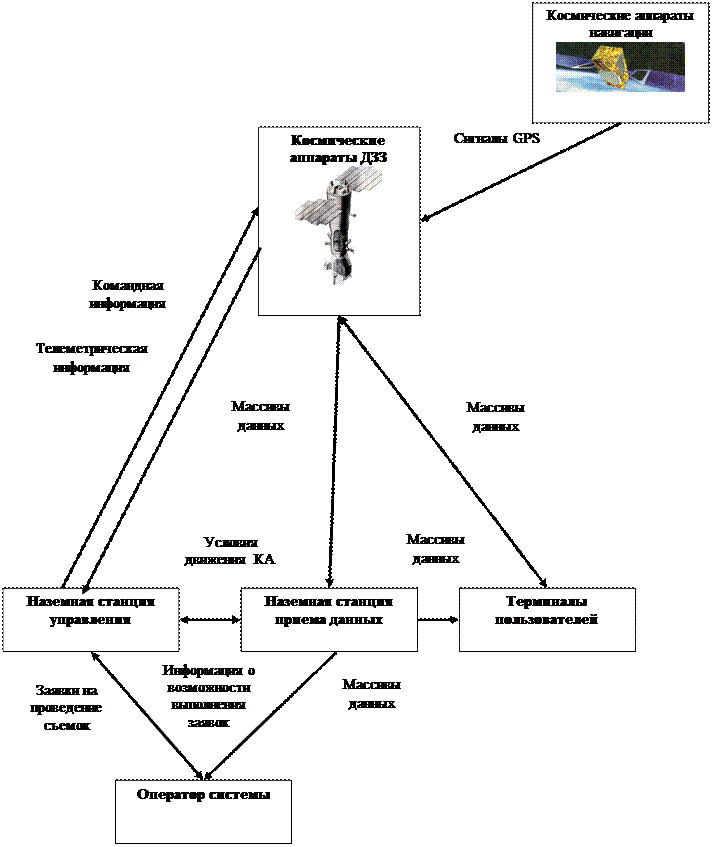
Космическая система наблюдения Земли – это совокупность функционально взаимосвязанных космических аппаратов и наземных технических средств, предназначенных для решения целевых задач. Структура системы представлена на рисунке 1.1, информационные потоки – на рисунке 1.2.

Основной функциональный элемент космической системы наблюдения Земли – космический аппарат (КА).

Космический аппарат как сложная техническая система имеет цель функционирования (наблюдение Земли и передача на Землю информации о результатах наблюдения), состоит из взаимосвязанных элементов, обеспечивающих выполнение цели системы, является элементом системы более высокого уровня (космической системы наблюдения Земли).

Внешней средой КА являются природное окружение (космическое пространство) и другие компоненты системы наблюдения Земли.

Структурно космический аппарат состоит из двух основных подсистем - полезной нагрузки – целевой аппаратуры (аппаратное и программное обеспечение, необходимые для получения требуемой информации) и платформы, обеспечивающей функционирование полезной нагрузки и передачу полученной информации на Землю (обслуживающая подсистема).

Полезная нагрузка КА

Состав целевой аппаратуры определяется задачами, возлагаемыми на космическую систему наблюдения Земли, и характеристиками объекта наблюдения (внешней средой).

Для получения данных о различных природно-хозяйственных объектах используются как пассивные (фотографические, оптико-механические и оптико-электронные, радиометрические, спектрометрические), так и активные (радиолокационные) системы в ультрафиолетовой (УФ), видимой (В), инфракрасной (ИК) и микроволновой (СВЧ, т.е. сверхвысокочастотной) областях спектра.

Платформа КА обеспечивает условия нормального функционирования полезной нагрузки: поддержание заданных параметров орбиты и ориентации КА, обеспечение требуемых условий функционирования аппаратуры (электропитание, тепловой режим), выдачу полезной нагрузке команд управления, сбор целевой и телеметрической информации и передача ее на Землю, обеспечение конструктивной целостности и жесткости.

Основные подсистемы платформы:

- система управления;

- система ориентации и стабилизации;

- система электроснабжения;

- командно-измерительная система;

- аппаратура спутниковой навигации;

- система ориентации солнечных батарей;

- корректирующая двигательная установка;

- конструкция (включая бортовую кабельную сеть, антенны, систему отделения и терморегулирования).

Общие требования к конструкции:

- минимальный собственный вес;

- обеспечение требуемых углов обзора датчиков информационной аппаратуры и системы ориентации;

- система раскрытия панелей солнечной батареи должна отвечать требованиям безопасности и надежности, а компоновка этих панелей – обеспечивать минимально возможный момент инерции на валу привода СОСБ для снижения массы и энергопотребления последнего;

- обеспечение минимальных возмущающих моментов от светового и аэродинамического давления;

- конструкция должна обеспечивать удобство проведения монтажных, испытательных и отладочных наземных работ, не затрудняя доступ к приборам и кабельной сети;

- при размещении аппаратуры должно быть учтено условие минимизации протяженности кабельных связей для сокращения энергопотерь в проводах и обеспечения электромагнитной совместимости аппаратуры.

Наземная система (наземный сегмент) обеспечивает слежение за КА и управление ним, передачу команд приема и обработки информации полезной нагрузки и телеметрической информации, выдачу информации потребителям. Типовые компоненты наземного сегмента: комплекс управления, комплекс приема, обработки и распространения информации, центр планирования съемок, их архивации.

Если в состав системы наблюдения входит не один космический аппарат, то их совокупность образуют отдельную подсистему – орбитальную группировку. КА в этом случае создается на базе унифицированной космической платформы.

В состав космической системы наблюдения Земли могут входить и ракетно-космические комплексы для создания и поддержания орбитальной группировки системы.

Космическая система есть единый сложный многокомпонентный многофункциональный распределенный в практически неограниченном по объему трехмерном пространстве. Отдельные компоненты космических систем могут одновременно являться компонентами других систем.

Как кибернетическая система космическая система обладает следующими специфическими чертами:

Является распределенной;

обладает высокой степенью автоматизации, имеет высокий удельный вес информационной составляющей, техническое и технологическое разнообразие;

обладает высокой устойчивостью функционирования;

подсистемы функционируют в условиях неопределенности относительно внешней среды;

является перманентно развивающейся системой;

носит ярко выраженный инновационный характер.

С точки зрения теории систем орбитальная группировка является именно системой, а не просто совокупностью КА: задачи КА и орбитальной группировки принципиально различны. Один КА не способен обеспечить выполнение целевой задачи - выполнение целевой задачи космической системой может быть достигнуто только в результате совокупного функционирования КА.

Расположение элементов в пространстве не является случайным, задачи между КА строго распределены, функционирование отдельного КА в данный момент времени зависит от функционирования остальных КА и состояния всей системы, целевая информация от каждого отдельного КА включается в общий поток.

КА в орбитальной группировке находятся друг с другом в различных отношениях: по расположению в пространстве, по функциональным задачам и др. Орбитальная группировка представляет собой распределенный в пространстве искусственный многокомпонентный космический объект. Этот объект выполняет роль большой космической станции в космической системе.

Структура космической системы наблюдения Земли

Информационные потоки космической системы наблюдения Земли

Сложная социально-экономическая система

Под экономической системой понимается любая система, в которой действуют стоимостные или натуральные товарные переменные.

В качестве экономической системы может выступать отдельная фирма; техническая или технологическая система, учитывающая стоимость технических средств или продукции; отрасль промышленности; экономика государства.

Экономическая система, в которой действуют социальные факторы, называется социально-экономической. В частности, любая макроэкономическая система государства или региона не может не включать социальный сектор и поэтому является социально-экономической¹.

Международный стандарт ИСО 9000:2000 определяет организацию как группу работников и необходимых средств с распределением ответственности, полномочий и взаимоотношений.

Можно дать и другое определение: организация - это систематизированное, сознательное объединение действий людей, преследующих достижение конкретных целей.

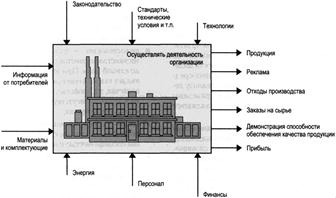
Связи системы-организации с внешней средой.

Создаваемая модель должна давать ответ на следующие вопросы:

• Кто из сотрудников организации должен выполнять конкретные функции?

• При каких условиях нужно выполнять функцию?

• Что должен сделать сотрудник в рамках данной функции?

• Каким образом следует ее выполнять?

• Какие ресурсы при этом необходимы?

• Каковы результаты выполнения функции?

• Какие информационные средства нужны?

• Каким образом все это согласовать?

• Как все это можно осуществить наиболее эффективно?

• Как можно изменить или построить бизнес-процесс?

• Как снизить риск и повысить эффективность изменений?

2 МЕТОДОЛОГИЯ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

2.1 Математическая модель, математическое моделирование – основные понятия, термины и определения

Термин «математическое моделирование» охватывает методологически малосвязанные разработку модели и ее использование. Иногда моделированием называется каждый из этих двух этапов в отдельности.

Математическое моделирование - процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта.

Математические модели относятся к знаковым моделям.

Один из аспектов математического моделирования как способа познания - изучение системы, явления с помощью вычислительного эксперимента (в таком понимании термин "вычислительный эксперимент" может быть синонимом термина "математическое моделирование").

Многие задачи исследования систем трудно достаточно хорошо формализовать и свести к математическим моделям, позволяющим ставить и решать поставленные задачи. Системный исследователь должен уметь формализовать в математических терминах конкретную задачу исследований - разработать математическую модель. Непонимание (или неумение четко поставить задачу) часто приводит к «победе математики над разумом».

Математическая модель как средство познания, исследования реального мира формируется на основании общей методологии системных исследований.

Математическая модель – описание в виде математических соотношений (например, формул, уравнений, неравенств, логических условий, операторов) состояния, изменения, протекания процессов в системе или явлении (в том числе функционирования системы), в зависимости от параметров системы, входных сигналов, начальных условий и времени.

Математическая модель — это „эквивалент“ объекта, отражающий в математической форме важнейшие его свойства — законы, которым он подчиняется, связи, присущие составляющим его частям.

Математическая модель - абстрактное математическое представление процесса, устройства или теоретической идеи; оно использует набор переменных, чтобы представлять входы, выходы и внутренние состояния, а также множества уравнений и неравенств для описания их взаимодействия. (Определение основано на идеализации «вход — выход — состояние», заимствованной из теории автоматов).

Вид математической модели зависит как от природы реального объекта, так и от задач исследования объекта, требуемой достоверности и точности решения этой задачи. Математическая модель отражает именно те особенности, которые необходимо исследовать для решения поставленной задачи.

Обычно математическая модель только приближенно описывает поведение реальной системы, являясь ее абстракцией, так как знания о реальной системе никогда не бывают абсолютными, а гипотезы часто вынужденно или намеренно не учитывают некоторые факторы.

Для поддержки математического моделирования разработаны компьютерные системы моделирования, например, Matlab, Matcad и др. Они позволяют создавать формальные и блочные модели как простых, так и сложных процессов и устройств и легко менять параметры моделей в ходе моделирования. Блочные модели представлены блоками (чаще всего графическими), набор и соединение которых задаются диаграммой модели.

Универсальность моделей: принципиально разные реальные явления могут описываться одной и той же математической моделью. На одной и той же модели могут быть изучены большое число вариантов её поведения (путем изменения параметров). Например, колебательные процессы, имеющие совершенно разную природу описываются одинаковой математической моделью - мы изучаем сразу целый класс описываемых ею явлений.

Основная задача математического моделирования: по заданным входным параметрам найти значения выходных параметров системы.

Модель — закономерность, преобразующая входные значения в выходные: Y = M(X). Под этим можно понимать таблицу, график, выражение из формул, закон (уравнение) и т. д. Это вопрос способа записи закономерности. Y - некоторый интересующий исследователя показатель.

На этом основании при определении понятия "математическая модель" используется широкое понятие оператора – функция, алгоритм, совокупность правил, обеспечивающие установление выходных параметров по заданным входным параметрам.

Математическую модель можно рассматривать как некоторый математический оператор и сформулировать понятие математической модели следующим образом.

Математическая модель – любой оператор (правило) А, позволяющий по значениям входных параметров x установить соответствующие выходные значения параметров y системы:

А: x → y, x ÎX, y ÎY.

Такое широкое определение включает в себя не только все многообразие математических моделей, но и информационные модели – процедуру поиска данных в базе данных можно представить в виде некоторого оператора. В таком контексте информационная модель – специфическая форма математической модели.

Основные понятия в моделировании систем определяются из соответствия аналогичным понятиям системы: элемент системы, связь, внешняя среда.

Моделирование как метод исследования имеет следующую структуру: постановка задачи, создание модели, исследование модели, перенос знания с модели на оригинал.

Модель может быть сосредоточена на функциях системы (функциональная модель) или на ее объектах (модели данных).

Функциональные модели выделяют события в системе, представляют с требуемой степенью детализации систему функций, которые в свою очередь отражают свои взаимоотношения через объекты системы.

Модели данных выделяют объекты системы, которые связывают функции между собой и с их окружением и представляют собой подробное описание объектов системы, связанных системными функциями.

Дата добавления: 2014-08-04; просмотров: 848; Нарушение авторских прав

Мы поможем в написании ваших работ!