Модели систем автоматического управления

Система автоматического управления стремится сохранить в допустимых пределах отклонения (рассогласования) ошибки между требуемыми и действительными значениями управляемых переменных при помощи их сравнения на основе принципа обратной связи и использования получающихся при этом сигналов для управления.

При автоматическом управлении качество процесса управления обеспечивает регулятор: обеспечивает поступление управляющих сигналов в зависимости от возмущающих воздействий, заданную точность работы в установившемся режиме, заданные динамические свойства системы (уменьшение ошибки, демпфирование колебаний).

Дадим основные определения системы автоматического управления на примере регулирования температуры в электропечи для закалки металла.

При автоматическом управлении воздействие на управляемый орган осуществляет специальное управляющее устройство.

Для построения автоматического управления технологическим процессом необходимо реализовать (вместо человека) управляющее устройство (двигатель), которое могло бы изменять состояние органа управления (передвигать рукоятку реостата) в зависимости от сигнала измерительного элемента (термопары).

Поскольку на выходе измерительного элемента имеет место сигнал небольшой мощности (ее хватает для изменения положения стрелки прибора, но недостаточно для питания двигателя), необходимо ввести промежуточное звено – усилитель мощности.

Ниже представлена функциональная схема автоматического управления процессом закаливания в электропечи.

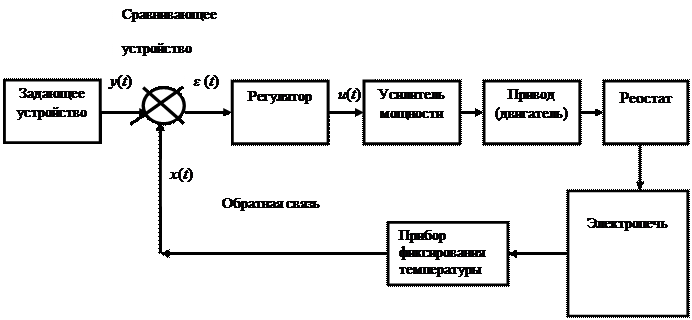
Сигнал у (t) (заданная температура) – управляющая переменная, сигнал х (t) (реальная температура) – управляемая переменная.

Система автоматического управления представляет собой совокупность объекта управления (электропечь) и управляющего устройства (усилитель, реостат, измерительное устройство, сравнивающее устройство), обеспечивающего процесс управления.

Управляющее устройство осуществляет целенаправленное воздействие на управляемую переменную (температуру). Устройство выполняет вычислительные функции, слабо связанные с физической природой объекта управления. Алгоритм его работы определяется динамическими свойствами управляемого процесса (математической моделью объекта) и задачами системы управления. Современные устройства управления представляют собой универсальные или специализированные средства вычислительной техники. Их программное обеспечение составляют системные средства и специальные прикладные программы, осуществляющие расчет управляющих воздействий u(t).

Для улучшения качества управления (уменьшения колебания процесса) в систему вводят дополнительный элемент – регулятор. При проектировании систем автоматического управления параметры усилителя мощности, привода, управляющего органа (реостата) остаются неизменными, изменяется только регулятор. На практике неизменную часть называют объектом управления (регулирования), а к управляющему устройству относят только изменяемую часть – регулятор. Именно его параметры изменяются в процессе проектирования САУ.

Система, у которой сигнал у (t) – известная функция (детерминированный сигнал) на всем промежутке управления, называется системой программного управления.

Система, у которой задающее воздействие у (t) = const называется системой стабилизации.

Система, у которой задающее воздействие у (t) – случайная функция, называется следящей системой.

Задающее устройство (задает нужное изменение параметров) преобразует воздействие в сигнал у (t), а сравнивающее устройство путем сравнения сигнала у (t) и регулируемой величины х (t) (предполагается, что измерительный элемент и элементы обратной связи не искажают сигнал х (t)) вырабатывает сигнал ошибки ε (t). Иногда сравнивающее устройство называют датчиком ошибки, отклонения или рассогласования.

Регулятор служит для обеспечения заданных динамических свойств замкнутой системы. С его помощью обеспечивается высокая точность работы в установившемся режиме, демпфируются колебания для сильно колебательных объектов (например, летательных аппаратов). Введение в систему регулятора позволяет устранить незатухающие или возрастающие колебания управляемой величины. Иногда регуляторы вырабатывают сигналы (команды) в зависимости от возмущающих воздействий, что существенно повышает точность систем.

В хорошо спроектированной системе ошибка ε (t) должна быть мала. Вместе с тем на объект должны поступать достаточно мощные воздействия. Мощности же сигнала ε (t) совершенно недостаточно для питания даже небольшого двигателя. В связи с этим важным элементом САУ является усилительное устройство, предназначенное для усиления мощности сигнала ошибки ε (t). Усилитель управляет энергией, поступающей от постороннего источника (электронные, гидравлические, пневматические усилители).

Исполнительные устройства предназначены для воздействия на управляющий орган (электрические, пневматические, гидравлические).

Чувствительные или измерительные элементы (датчики) преобразуют управляемые переменные в сигналы управления (например, преобразования вида "угол – напряжение"). Объектом управления считается вся неизменная часть системы (все элементы, кроме регулятора) – электрическая печь, ядерный реактор, самолет, ракета и т.д. Управляемые переменные – напряжение, число оборотов, угловое положение, курс, мощность и т.д.

Одномерные системы могут быть системами программного управления, системами стабилизации и следящими системами.

Кроме того, встречаются системы: системы с поиском экстремума показателя качества, системы оптимального управления, адаптивные системы.

Первый этап исследования или проектирования систем автоматического управления, как и любых других систем, - неформальный этап – построение описательной, содержательной модели.

Математическая модель регулятора

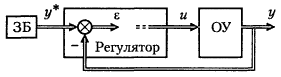
Регуляторы и задающие блоки. В состав устройства управления системы, предназначенной для решения локальных задач, входят задающий блок (ЗБ) и регулятор выходных переменных.

В современных системах блоку не обязательно соответствует физическое устройство. Это может быть и алгоритм или программа расчетов требуемых переменных (сигналов).

Регулятором называется блок (алгоритм), рассчитывающий управляющее воздействие u(t) с целью решения локальной задачи управления. Алгоритмом управления называется набор аналитических выражений, используемых для расчета управляющих воздействий, или система операций, выполняемых по определенным правилам.

Типовой алгоритм управления, это математическая зависимость между выходным регулирующим воздействием u(t) и входным отклонением ε регулируемой величины y от заданного значения y*. Простейшими алгоритмами управления (регуляторами) являются регуляторы отклонения вида: u(t) = U(e(t)). В практике принято рассматривать три типовых закона регулирования: пропорциональный, интегрирующий, дифференцирующий. На базе этих законов в регуляторах реализуют более сложные алгоритмы, являющиеся комбинацией основных: пропорционально-интегральный, пропорционально-дифференциальный, пропорционально-интегрально- дифференциальный, и т.п.

Уравнение пропорционального регулятора: u(t) = k_пe(t), W(p) = k_п.

Уравнение интегрального регулятора: u(t) = k_и 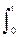e(t) dt, W(p)

где: k_п, k_и - постоянные коэффициенты,

W(p) – передаточная функция системы - отношение выходного сигнала к входному сигналу при нулевых начальных условиях (не зависит от самих сигналов, зависит только от самих дифференциальных уравнений и обладает свойством линейности).

Математическая модель объекта управления

Математическая модель САУ (операторное уравнение) устанавливает количественную связь между входом и выходом системы.

Для обозначения входных и выходных сигналов воспользуемся обозначениями, характерными для объекта управления, где входным сигналом является управляющее воздействие u(t), а выходным регулируемая переменная y(t).

В общем случае модель одноканального объекта управления описывается нелинейным дифференциальным уравнением (системой уравнений), связывающим входной сигнал управления u(t) и выходной сигнал состояния объекта y(t):

F(y', y", …, y⁽ⁿ⁾, u', u", …, u^(m)) = 0. (1)

Уравнение описывает динамическое состояние ОУ на некотором временном интервале t≥t_o, и связывает входные сигналы u(t) и их производные u^(m)(t) с выходными сигналами y(t) и их производными y⁽ⁿ⁾(t). В большинстве случаев операторное уравнение системы принадлежит к классу дифференциальных уравнений или эквивалентных им интегральных уравнений.

Для получения дифференциального уравнения системы в целом обычно составляют описания отдельных ее элементов, т.е. составляют дифференциальные уравнения для каждого входящего в систему элемента (например, для САУ электропечи составляются дифференциальные уравнения усилителя, привода, реостата, электропечи, термопары и элемента сравнения).

Задачей системы автоматического управления является изменение переменной у (t) согласно заданному закону с определенной точностью (с определенной ошибкой).

При проектировании систем автоматического управления необходимо выбрать такие параметры системы, которые обеспечили бы требуемую точность управления. Кроме этого, параметры системы должны обеспечить требования устойчивости и регулярности поведения системы в переходном процессе.

Типовой алгоритм управления, это математическая зависимость между выходным регулирующим воздействием u(t) и входным отклонением ε регулируемой величины y от заданного значения y*. Входной величиной для регулятора является сигнал ε, а выходной – регулирующее воздействие u:

u(t) = U(e(t),у*(t),...).

В качестве оператора U(•) могут выступать как алгебраические и трансцендентные функции, так и интегро-дифференциальные операторы, булевы функции и пр.

В общем случае процессы, происходящие в системах автоматического управления, описываются нелинейными дифференциальными уравнениями, которые могут быть решены лишь в отдельных частных случаях. Для большого числа систем эти уравнения могут быть линеаризованы.

Переход к линейным дифференциальным уравнениям выполняется операцией линеаризации, при которой переменные уравнения (1) заменяются новыми переменными – отклонениями от некоторого номинального режима (y=y-y_н, u= u-u_н), начало координат переносится в точку номинального режима, а функция F раскладывается в ряд Тейлора в окрестностях этой точки по частным производным. В результате линеаризации получаем следующую систему линейных уравнений в отклонениях:

A₀(t)y⁽ⁿ⁾ + A₁(t)y^(n-1) +…+ A_n(t)y = B₀(t)u^(m) + В₁(t)y^(m-1) +…+ B_m(t)u. (2)

Порядок системы уравнений равен n по порядку производной y⁽ⁿ⁾(t), n ≥ m, так как при n < m системы технически нереализуемы.

В случае постоянных коэффициентов система называется стационарной.

При этом процессы в САУ будут описываться линейными дифференциальными уравнениями:

a_n dⁿу/dtⁿ + a_n-1 d^n-1у/dt^n-1 +…. + a₀у = b_m d^mg/dt^m +…. + b₀g (3)

где a_j, b_j – постоянные коэффициенты (параметры) модели, a₀ > 0, b₀ > 0, n - порядок модели, 0 ≤ m < n. Решение уравнений таких стационарных объектов относительно y(t) является главным объектом исследований в классической теории автоматического управления.

Решение даже линейного уравнения связано с вычислительными трудностями. Поэтому для анализа линейных САУ используют метод, основанный на преобразовании Лапласа.

В стационарных системах коэффициенты дифференциального уравнения a_i, b_i – постоянные величины.

После преобразования Лапласа

(a_npⁿ + a_n-1p^n-1 _{+ ….+}a₀)x(p) = (b_mp^m + b_m-1p^m-1 _{+ ….+} b₀)g(p),

где:

x(p) – преобразование Лапласа выходного сигнала системы;

g(p) – преобразование Лапласа входного сигнала.

Часто у(p) и g(p) называют изображениями сигналов у(t) и g(t).

Передаточная функция системы.

Для линейного уравнения преобразование Лапласа отношения выходного сигнала Y(p) к входному сигналу U(p) при нулевых начальных условиях не зависит от самих сигналов и называется передаточной функцией системы W(p).

Y(p) = U(p) (b₀p^(m) + b₁p^(m-1) +…+ b_m) /(a₀p⁽ⁿ⁾ + a₁p^(n-1) +…+ a_n),

W(p) = (b₀p^(m) + b₁p^(m-1) +…+ b_m) /(a₀p⁽ⁿ⁾ + a₁p^(n-1) +…+ a_n), (3.2.5)

Y(p) = W(p) U(p).

Передаточная функция W(p) зависит только от самих дифференциальных уравнений и обладает свойством линейности:

Если Y(p) = Y₁(p) + Y₂(p), то U(p) = W(p)Y₁(p) + W(p)Y₂(p) = U₁(p)+U₂(p).

Если Y(p) = сY(p), то U(p) = W(p) Y(p) = с W(p) Y(p).

В общем случае замкнутая система регулирования с обратной связью рассматривается в структурной форме, приведенной на рис. 3.2.1, где используются следующие обозначения сигналов:

Y(p) = W(p)e(p); W(p) = W₁(p)W₂(p);

Y_ос(p) = W_ос(p)Y(p); e(p)=U(p)-Y_oc(p).

Выражение выходного сигнала состояния системы через входной сигнал управления:

Y(p)=W(p)(U(p)-W_ос(p)Y(p);

Y(p)(1± W(p)W_ос(p))=W(p)U(p).

Отсюда главная передаточная функция замкнутой системы:

W_зс(p) = Y(p)/U(p) = W(p)/[1 ± W(p) W_oc(p)].

Знак плюс или минус определяется типом обратной связи (отрицательная или положительная). Соответственно, выходной сигнал с учетом сигнала дестабилизирующего воздействия f(t), который суммируется с правой частью выражения (3.2.3):

Y(p)=W_зс(p)U(p) + W_f(p)f(p),

где W_f(p) – передаточная функция по возмущению. В замкнутой системе передаточная функция по возмущению определяется как отношение выходной величины, преобразованной по Лапласу, к функции возмущающего воздействия, преобразованной по Лапласу при нулевых начальных условиях. Возмущающее воздействие может быть приложено к любой точке системы.

W_f(p) = Y(p)/f(p) = W₂(p)/[1+W_oc(p)W(p)].

Передаточная функция по ошибке:

W_e(p) = e(p)/U(p) = 1/[1 + W(p) W_oc(p)].

Передаточная функция по ошибке - основное средство исследования точности САУ. C учетом возмущающего воздействия:

e(p)=W_e(p)U(p) + W_ef(p)f(p),

где W_ef(p) - передаточная функция по ошибке и возмущению (от возмущения к ошибке):

W_ef(p) = e(p)/f(p) = -W₂(p)W_oc(p)/[1 + W(p) W_oc(p)].

Передаточная функция по обратной связи:

W_Yoc(p) = Y_oc(p)/U(p) = W(p) W_oc(p)/[1 + W(p) W_oc(p)].

Соединение звеньев

Любая, даже самая сложная, система автоматического управления состоит из элементарных (типовых) звеньев. Характеристики этих звеньев хорошо изучены. Соединяясь между собой различным образом, типовые звенья образуют САУ.

Модель вход-выход строится по известным уравнениям отдельных компонентов (блоков, звеньев). Процедура сводится к преобразованию системы дифференциальных уравнений, описывающих поведение отдельных блоков, к единому уравнению системы управления.

Существуют три основных вида соединений: последовательное, параллельное и с обратной связью.

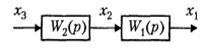
Последовательное соединение блоков. При последовательном соединении звеньев выходная величина предыдущего звена является входной для последующего. При известных передаточных функциях звеньев, можно записать:

X₂(p) = W₂(p) X₃(p), X₁(p) = W₁(p) X₂(p) = W₁(p)W₂(p)X₃(p).

W(p) = W₁(p) W₂(p).

Таким образом, систему из неограниченного количества звеньев, включенных последовательно, можно заменить одним эквивалентным звеном с передаточной функцией W(p) равной произведению передаточных функций звеньев.

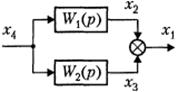
Параллельное соединение блоков. При параллельном соединении звеньев на все входы подается одна и та же величина, а выходная величина равна сумме выходных величин отдельных звеньев.

X₂(p) = W₁(p) X₄(p), X₃(p) = W₂(p) X₄(p).

X₁(p) = X₂(p)+X₃(p) = (W₁(p)+W₂(p)) X₄ (p).

W(p) = W₁(p)+W₂(p).

Из последнего выражения следует, что параллельное соединение звеньев эквивалентно одному звену с передаточной функцией, равной сумме передаточных функций, входящих в соединение звеньев.

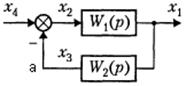
Система с отрицательной обратной связью. При встречно-параллельном соединении звеньев на вход звена кроме входной подается еще и выходная величина через специальное звено обратной связи. На рисунке звено W₁(p) составляет прямую цепь, которая охвачена ОС, звеном W₂(p). При этом если сигнал x₃ вычитается из входного сигнала x₄, то ОС называется отрицательной, а если суммируется, то ОС – положительная. Для отрицательной обратной связи можно записать:

X₁(p) = W₁(p) X₂(p), X₃(p) = W₂(p) X₁(p), X₂(p) = X₄(p) – X₃(p).

Решая эти три уравнения относительно X₁(p), находим:

X₁(p) = X₄(p) W₁(p) /(1+ W₁(p)W₂(p)).

Передаточная функция

W(p) = W₁(p) /(1+ W₁(p)W₂(p)). Полученная передаточная функция может интерпретироваться как передаточная функция последовательно соединенных звеньев с передаточной функцией W₁(p) и системы с передаточной функцией:

Ф(p) = 1/(1+W_рс),

где W_рс = W₁(p)W₂(p) - передаточная функция разомкнутой системы, например, в точке “а”.

При охвате любого звена единичной ОС (т.е. при W₂ (p) = 1) разомкнутая система преобразуется в замкнутую с передаточной функцией (из выражения (3.6.1)):

W(p) = W₁(p) /(1+ W₁(p)).

Дата добавления: 2014-08-04; просмотров: 956; Нарушение авторских прав

Мы поможем в написании ваших работ!