Модели автоматизированных систем управления

Всякая система управления с точки зрения ее функционирования решает три основные задачи: сбор и передача информации об управляемом объекте, переработка информации, выдача управляющих воздействий на объект управления.

Различают два основных типа автоматизированных систем управления: системы управления производственными процессами и системы организационно-экономического или административного управления.

Главные отличия этих двух типов – в характере объекта управления и форме передачи информации.

В системах управления технологическими процессами объекты управления – машины, процессы, приборы, устройства, форма передачи информации – различные сигналы (электрические, механические, световые и др.).

В организационно-экономических и административных системах управления объекты управления – человеческие коллективы, форма передачи информации – документы.

Интегрированные системы управления – объединение систем управления предприятием и технологическими процессами. Им присуще организация информационных процессов на предприятии и организация их выполнения. Объект управления – совокупность процессов, свойственных данному предприятию, по преобразованию ресурсов (материалы, оборудование, энергетические, трудовые, финансовые ресурсы) в готовую продукцию.

Особенности таких систем, обуславливающие их сложность: большое число разнородных элементов и высокая степень их взаимосвязи в процессе производства, неопределенность результатов выполнения многих процессов (брак, сбои, несвоевременные поставки, нерегулярность спроса), нестационарность предприятия (постоянное изменение и развитие предприятия, сложность работы с людьми).

Среди систем управления этого типа могут быть выделены системы управления обслуживанием на транспорте (оперативное обслуживание пассажиров, повышение загрузки транспортных средств, контроль операций и др.), системы контроля (проверка оборудования, диспетчеризация и др.).

Информационные и управляющие системы предприятий и отраслей оперируют интенсивными потоками информации (ввод, переработка, преобразование информации) и структурированы исходя из задач обеспечения информацией и управления.

Осведомительная информация о воздействиях внешней среды поступает к средствам передачи информации, которые ее трансформируют (кодирование, декодирование, задержки во времени, внесение дополнительных ошибок и помех и т.д.) и передают средствам обработки информации (центральным или периферийным). Здесь производится первичная сортировка и местная обработка информации и запоминание ее в устройствах памяти системы управления.

Это позволяет провести окончательную обработку информации, решить задачи планирования работы системы и выработать управляющие сигналы для исполнительных органов.

Исполнительные органы изменяют характеристики управляемых объектов в соответствии с сигналами, полученными от средств переработки информации.

Изменение характеристик управляемых объектов обнаруживают и измеряют датчики информации. Эти отклонения вместе с информацией о новых воздействиях внешней среды используются для выработки новых управляющих сигналов и т. д.

Для математического описания сложной системы с автоматизированным управлением удобно использовать схему агрегатов и агрегативных систем, когда каждый из элементов (датчики информации, средства передачи и т. д.) описывается в виде агрегата, а система в целом - как агрегативная система. В этом случае исчерпывается и вопрос о методике моделирования системы.

Процессы управления во всех случаях характеризуются наличием информационных потоков; однако системы управления, которые связаны с обработкой особенно интенсивных информационных потоков получили название «информационных». Структура этих систем обеспечивает оптимальный сбор, хранение, переработку и выдачу больших массивов информации.

В класс информационных не включаются системы управления технологическими процессами, работающие в истинном масштабе времени с реальными объектами (управление станками, металлургическими процессами, химическими реакторами и т. д.).

К информационным системам обычно относят системы управления крупными предприятиями в целом, решающие задачи перспективного и текущего планирования, а также задачи оперативного управления производством (скорее не на технологическом, а на организационном уровне). Информационные системы более крупного масштаба могут быть использованы для управления группой предприятий, отраслью или экономикой в целом.

Существуют информационные системы и другого целевого назначения: диагностические (как медицинские, так и технические), библиографические, диспетчерские и т. д.

Обобщенная схема процесса, приводящая к решению задачи планирования, имеет следующий вид.

В информационную систему поступают заявки, которые отражают потребность в материально-технических средствах. Эти данные сортируются, суммируются и фиксируются в накопителе системы. Одновременно поступают текущие донесения от потребителей и поставщиков о наличии и движении материально-технических средств, которые также фиксируются в системе.

По имеющимся в системе данным о наличии материально-технических средств производится сопоставление потребностей с имеющимися в наличии материально-техническими средствами в текущем производстве и у потребителей.

С учетом запроса потребителей, наличия материально-технических средств и плана заказов производится оптимальное распределение материально-технических средств (план снабжения).

Модель, предназначенная для оценки качества управления, должна быть моделью системы в целом, достаточно подробно описывающей функционирование как управляющих, так и управляемых объектов.

Модели автоматизированных систем управления производственными процессами

Управление производственным процессом основано на использовании системы автоматизированного управления, целью такого управления является улучшение технических и экономических показателей производственного процесса и предприятия в целом.

Основой создания системы управления предприятием является разработка модели управления производственными процессами.

При выборе структурной схемы и алгоритма управления АСУ ПП существенной является информация о состоянии производственного процесса с учетом его динамических свойств не только в текущий, но и в прошедшие моменты времени.

Большая размерность входов и выходов, сложная структура и неопределенность преобразований входных потоков, случайные изменения преобразований приводят к необходимости применения имитационного моделирования для оценки качества системы управления. Учитываются погрешности измерений, степень достоверности результатов в условиях большого объема информационных потоков, что также требует применения имитационного моделирования.

Модели автоматизированных систем управления предприятием

Предприятие представляется в виде совокупности взаимосвязанных функциональных подсистем и управляющих звеньев, обеспечивающих производственную деятельность.

Подсистемы производственной деятельности обеспечивают выполнение:

- основных производственных процессов по выпуску основной и вспомогательной продукции,

- обслуживающих процессов (ремонтные, энергетические, транспортные службы), процессов развития внедрение новой техники, строительство, интеллектуальные разработки).

Обеспечивающие подсистемы: основные и оборотные фонды (материальные ресурсы многоразового и одноразового использования), трудовые ресурсы (организация труда, зарплата, подготовка кадров), интеллектуальные ресурсы (научные исследования), подсистемы, обеспечивающие финансовую деятельность, маркетинг.

Информационные и управляющие системы таких комплексов оперируют интенсивными потоками информации (ввод, переработка, преобразование) и структурированы исходя из задач информации и управления.

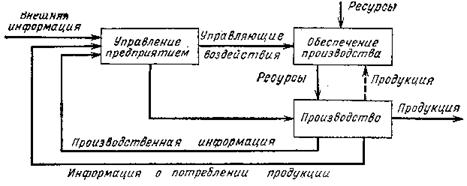
Предприятие рассматривается как динамическая модель системы с управлением, которая объединяет в единой схеме с обратными связями все аспекты функционирования.

Рассматриваются взаимосвязанные потоки: материалов, заказов, денежных средств, оборудования, рабочей силы.

Сущность производственных процессов: преобразование материальных, энергетических, финансовых, трудовых ресурсов в продукт, оцениваемый экономическими показателями (например, себестоимостью). При этом учитываются все возмущения, отклоняющие производственный процесс от заданных условий: возмущающие факторы внешней среды (первичны) и возмущающие факторы, обусловленные внутренними связями.

Возмущающие факторы внешней среды:

- технологические отклонения параметров процессов и средств труда;

- организационные и информационные возмущения, связанные с несовершенством организации производства, планирования, обработки и отображения информации;

- социальные – колебания индивидуальной производительности (заболевания, нарушения дисциплины).

Возмущения, обусловленные внутренними связями:

- организационные и технологические связи: возмущения на входе одного объекта (брак) вызывает возмущение на других объектах;

- возмущения процесса управления: управление одним элементом (устранение возмущения) вызывает возмущение в другом).

Динамическое моделирование предприятия представляет собой изучение деятельности предприятия как информационной системы с обратной связью. На вход производственного процесса поступают ресурсы, на выходе – готовая продукция.

Цель управления - улучшение технических и экономических показателей производственного процесса и предприятия в целом.

Критериями оценки качества управления могут быть себестоимость, качество продукции.

Система управления решает три основные задачи: сбор и передача информации об управляемом объекте, переработка информации, выдача управляющих воздействий на объект управления.

Большая размерность входов и выходов, сложная структура и неопределенность преобразований входных потоков, случайные изменения преобразований приводят к необходимости применения имитационного моделирования для оценки качества системы управления.

Алгоритм управления предполагает установление соотношений между информацией о состоянии процесса, вводимой в управляющее устройство и управляющим воздействием, поступающим из управляющего устройства на вход процесса.

Системы управления производственной деятельностью предприятия основаны на автоматизации информационных процессов предприятия.

Системы управления производством эффективны только при условии создания единой схемы движения информации от первичной до выдачи информации управляющим органам. Для этого необходим единый комплекс взаимоувязанных моделей различных уровней планирования и производства.

Различают два основных типа автоматизированных систем управления: системы организационно-экономического или административного управления и системы управления технологическими процессами.

Главные отличия этих двух типов – в характере объекта управления и форме передачи информации.

В организационно-экономических и административных системах управления объекты управления – человеческие коллективы, форма передачи информации – документы.

В системах управления технологическими процессами объекты управления – машины, процессы, приборы, устройства, форма передачи информации – различные сигналы (электрические, механические, световые и др.).

Интегрированные системы управления – объединение систем управления предприятием и технологическими процессами. Им присуще организация информационных процессов на предприятии и организация их выполнения.

Объект управления – совокупность процессов, свойственных данному предприятию, по преобразованию ресурсов (материалы, оборудование, энергетические, трудовые, финансовые ресурсы) в готовую продукцию.

Особенности таких систем, обуславливающие их сложность: большое число разнородных элементов и высокая степень их взаимосвязи в процессе производства, неопределенность результатов выполнения многих процессов (брак, сбои, несвоевременные поставки, нерегулярность спроса), нестационарность предприятия (постоянное изменение и развитие предприятия, сложность работы с людьми).

Среди систем управления этого типа могут быть выделены системы управления обслуживанием на транспорте (оперативное обслуживание пассажиров, повышение загрузки транспортных средств, контроль операций и др.), системы контроля (проверка оборудования, диспетчеризация и др.).

Информационные и управляющие системы предприятий и отраслей оперируют интенсивными потоками информации (ввод, переработка, преобразование информации) и структурированы исходя из задач обеспечения информацией и управления.

Предприятие представляется как комплекс сетей каналов информации на основе пунктов контроля реальных процессов (производство, сбыт, строительство, наем рабочей силы).

Каждому пункту деятельности предприятия соответствует пункт принятия решений, основанных на информации из внутренних и внешних источников. Принятое решение управляет действием и является источником новой информации.

В каждом из трех элементов (решение – действие – информация) имеют место запаздывания (для выполнения каждого из них необходимо время), выходы их элементов могут быть неадекватны входу (усиления или ослабления), могут быть искажения или шумы. Любая точка системы может быть чувствительнее к одним видам возмущений по сравнению с другими.

Решения принимаются на многих уровнях – системы управления предприятиями имеют иерархическую многомодульную структуру.

Основные этапы создания АСУ:

- технико-экономический анализ и выбор степени автоматизации исходя их целей управления (улучшение технико-экономических показателей производственного процесса);

- моделирование производственного процесса как объекта управления;

- разработка алгоритмов управления (принятия решений) и структуры системы;

- техническая реализация системы.

Между этапами существует связь, что обуславливает циклический характер разработки системы с постепенным усложнением и уточнением модели. Такое комплексное рассмотрение всех этапов представляет собой системный подход к проектированию АСУ.

Большая размерность входов и выходов, сложная структура и неопределенность преобразования входных потоков приводят к необходимости применения имитационного моделирования для оценки качества системы управления.

9 МОДЕЛИРОВАНИЕ ПРОИЗВОДСТВЕННЫХ ПРОЦЕССОВ

Общая характеристика производственного процесса

Производственный комплекс для поточного выпуска штучных изделий (автомобилей, самолетов, труб, часов и т.д.) формализуется как дискретный производственный процесс. К производственным комплексам дискретного типа можно отнести крупные морские, и авиационные порты, железнодорожные станции с оборудованием погрузки-разгрузки, технического обслуживания и др.

Производственный комплекс состоит из большого количества станков, обеспечивающих выполнение технологических операций (обработка деталей, сборка узлов, агрегатов, изделий). Технологические операции объединяются в технологические линии. Работа станков, операций, линий характеризуется частичной или полной синхронизацией и взаимозависимостью режимов выполнения операций. Средства управления производственным процессом (датчики, линии передачи данных, вычислительные устройства) собирают, обрабатывают информацию и вырабатывают управляющие команды.

Под процессом понимается последовательность действий (операций), направленных на получение определенных свойств системы или на достижение определенного ее состояния. Выделим производственные процессы – всю совокупность основных технологических процессов (изготовление, сборка, испытание) и сопутствующих процессов (планирование, организация, транспортировка, хранение), осуществляемых с целью превращения материалов и полуфабрикатов в готовые изделия.

Производственный процесс является примером сложной системы со всеми присущими ей свойствами. При проектировании на системном уровне таких сложных систем как транспортные системы, вычислительные системы и сети, производственные и технологические процессы, производственные предприятия, автоматизированные системы проектирования и управления требуется выбор оптимального (рационального) процесса их функционирования.

Технологические процессы как часть производственного процесса содержат действия по изменению и последующему определению состояния предмета производства. Технологические процессы строятся по отдельным способам выполнения процесса (технологические процессы механической обработки, термической обработки, обработки давлением, сварки, пайки, литья и т.д.) и по объектам производства (технологический процесс изготовления отдельных подсистем - кузова, двигателя, сборки объекта в целом).

Производственная (технологическая) операция – законченная часть технологического процесса, выполняемая на данном рабочем месте. Результатом любой технологической операции является превращение одного объекта (или совокупности объектов) с определенными свойствами в другой объект с иными свойствами. Технологическая операция является основной единицей планирования производства, учета производительности, управления и контроля технологического процесса.

Проектирование технологического процесса предполагает определение такой последовательности технологических операций (управление), которая позволит получить конечный продукт с наибольшей эффективностью (например, при минимальных экономических затратах).

Поскольку технологические операции реализуются на основании фундаментальных законов механики, физики, химии и др., то может быть создана математическая модель процесса. Переход системы из одного состояния в другое может представлять собой, например, химическое превращение одной совокупности веществ в другую, управляющими переменными могут быть температура, давление, продолжительность реакции и т.д.

В общем виде математическая модель любой технологической операции характеризуется начальным и конечным состояниями, управлениями, оператором перехода из начального состояния в конечное. В оператор перехода могут быть также включены экономические показатели.

Большинство технологических операций можно выполнить с использованием разных методов обработки и оборудования. Выбор рационального варианта осуществляется на основе технико-экономического анализа возможных в данных производственных условиях вариантов.

При проектировании производственных процессов в системе исследуются такие параметры, как производительность (пропускная способность) проектируемой системы, продолжительность обслуживания в системе, эффективность используемого оборудования. Входные величины при исследованиях чаще всего являются случайными, и анализ их функционирования на системном уровне носит статистический характер. Основой анализа и оптимизации различных производственных процессов является имитационное моделирование. В первом приближении – при исследовании на качественном уровне - исследуемые системы могут формализоваться как системы массового обслуживания.

9.1 Модели систем массового обслуживания

Модели систем массового обслуживания (СМО) разработаны для описания широко распространенных сложных систем, назначением которых является обслуживание в широком понимании, причем, массовое. Такие системы реализуют многократное выполнение однотипных задач.

Широкое понимание массового обслуживания включает в себя все формы обслуживания во многих областях экономики, финансов, производства, в службе связи, в транспорте, в военном деле, в быту (обслуживание продавцами покупателей, продажа билетов в кассах, ремонтные работы), медицине (на дому, в поликлиниках), и т.п.

Примеры СМО: банки различных типов (коммерческие, инвестиционные, ипотечные, инновационные, сберегательные), страховые организации (государственные, акционерные общества, компании, фирмы, ассоциации, кооперативы), налоговые инспекции, различные системы связи (в том числе телефонные станции), погрузочно-разгрузочные комплексы (порты, товарные станции), автозаправочные станции, различные предприятия и организации сферы обслуживания (магазины, справочные бюро, парикмахерские, билетные кассы, пункты по обмену валюты, ремонтные мастерские, больницы).

Такие системы как компьютерные сети, системы сбора, хранения и обработки информации, транспортные системы, автоматизированные производственные участки, поточные линии, различные военные системы, в частности системы противовоздушной или противоракетной обороны также могут рассматриваться как своеобразные СМО.

В основе формализации сложной системы как системы массового обслуживания – выделение обслуживающей системы, к которой в случайные моменты времени поступают заявки на обслуживание. При этом определяются три основные понятия: кого (что) обслуживают, кто (что) обслуживает, как (по каким правилам) обслуживает.

Основные элементы систем массового обслуживания.

Анализ и прогнозирование поведения сложных объектов и процессов выполняется методами теории массового обслуживания.

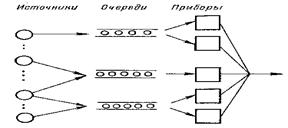
Основные компоненты системы обслуживания: входной поток, обслуживающая система, выходной поток.

Схематическая структура системы массового обслуживания

Система массового обслуживания представляет собой физическую систему дискретного типа с конечным (или счетным – можно пронумеровать) множеством состояний, система из одного состояния в другое переходит скачком, в момент, когда происходит какое либо событие (приход новой заявки, освобождение канала, уход заявки из очереди и т.д.). В любой момент времени система может быть в одном из этих состояний.

Во всякой СМО можно выделить следующие основные элементы: входной поток заявок; очередь; - каналы обслуживания (приборы); выходной поток обслуженных заявок.

Примеры: обслуживание большого количества однотипных требований (заявок, запросов на обслуживание) в телефонии, в системе продажи билетов. Заправочная станция: заявка на обслуживание – прибытие автомобиля (бензоколонки – обслуживающие каналы). Аэропорт: прибытие самолета (заявка), посадочные полосы (обслуживающие каналы).

Обслуживающая система – совокупность очередей и линий (каналов) обслуживания. Каждая заявка должна поступить на одну из обслуживающих линий, чтобы пройти соответствующее обслуживание. Так как в общем случае продолжительность обслуживания является случайной величиной, то заявкам приходится ожидать, пока не освободится обслуживающая линия. В этом случае они находятся в накопителе, образуя одну или несколько очередей.

Механизм обслуживания (характеристики процесса обслуживания): множество обслуживающих каналов (приборов), количество одновременно обслуживаемых требований, продолжительность и тип обслуживания (последовательное или параллельное функционирование приборов), число фаз обслуживания.

Роль каналов могут играть различные приборы, лица, выполняющие те или иные операции (кассиры, операторы, парикмахеры, продавцы), линии связи, автомашины, краны, ремонтные бригады, железнодорожные пути, бензоколонки и т.д.

Каждый канал одновременно может обслуживать только одну заявку и каждая находящаяся под обслуживанием заявка обслуживается только одним каналом.

Если каналы СМО однородны, т.е. выполняют одну и ту же операцию обслуживания, то такие СМО называются однофазными. Если каналы обслуживания расположены последовательно и они неоднородны, так как выполняют различные операции обслуживания, то СМО называется многофазной (заявка обслуживается несколькими устройствами).

Примером работы многофазной СМО может служить обслуживание покупателя в магазине, обслуживание автомобилей на станции техобслуживания (мойка, диагностирование и т.д.), технологический процесс обработки детали (определенная очередность операций).

Многоканальные СМО могут состоять из однородных каналов, либо из разнородных, отличающихся длительностью обслуживания одной заявки. Практически время обслуживания каналом одной заявки Т_об является непрерывной случайной величиной. Однако при условии абсолютной однородности поступающих заявок и каналов время обслуживания может быть и величиной постоянной (Т_об = const).

Возможные варианты: ограниченная вместимость очереди, перемещение либо заявок к приборам, либо приборов к заявкам, непрерывно работающие системы (даже при отсутствии заявок), обслуживание заявок фиксированными порциями, параллельная или последовательная работа приборов, число обслуживающих приборов зависит от состояния системы, приборы функционируют по согласованному регламенту, приборы реализуют специфические и взаимно незаменимые процедуры и т.д.

Режим работы системы зависит от характеристик потока заявок и от характеристик производительности самой системы: числа каналов и быстродействия каждого канала (времени обслуживания одной заявки).

В любой момент времени канал находится в одном из двух состояний – свободен или занят.

В некоторый момент времени t в систему поступает заявка. Если в этот момент времени имеются свободные каналы, заявка принимается к обслуживанию. В противном случае, т.е. когда все каналы заняты, заявка остается в систем в течение некоторого времени (τ_пр – время пребывания заявки в системе). За этот интервал времени она должна быть принята к обслуживанию, в противном случае считается потерянной – получает отказ.

Время обслуживания одной заявки может быть величиной как случайной, так и детерминированной, меняться от заявки к заявке. В общем случае – случайная величина.

Система с отказами при τ_пр = 0, система с ожиданием τ_пр = ∞, система с ограниченным ожиданием при 0 < τ_пр < ∞.

Заявка, принятая к обслуживанию занимает один из каналов в системе в течение времени обслуживания τ_з (время занятости канала). По окончании этого времени канал может приступить к обслуживанию новой заявки.

Обычно величины τ_пр и τ_з считаются случайными величинами с заданными законами (или совместным законом) распределения. Одна из них или обе могут быть фиксированы.

Случайный характер потока заявок и времени их обслуживания приводит к неравномерной загруженности СМО: в некоторые промежутки времени на входе СМО могут скапливаться не обслуженные заявки, что приводит к перегрузке СМО, в некоторые же другие интервалы времени при свободных каналах на входе СМО заявок не будет, что приводит к недогрузке СМО, т.е. к простаиванию ее каналов.

Заявки, скапливающиеся на входе СМО, либо "становятся" в очередь (т.е. образуют список объектов подлежащих обработке), либо по какой-то причине невозможности дальнейшего пребывания в очереди покидают СМО не обслуженными. Закон, определяющий порядок обслуживания входных заявок, называется дисциплиной очереди.

Примеры. Совокупность операций в почтовом отделении. В одном окне – продажа марок (часто и мало времени на обслуживание), прием заказных писем (реже и больше времени на обслуживание) и прием переводов (еще реже и много времени на обслуживание).

Отыскание неисправностей в телевизоре – направленный перебор (метод проб и ошибок). Если пробы независимы, то поток простейший. Это случай, когда обслуживание сводится к последовательности попыток, каждая из которых может закончиться положительным результатом (обстрел цели).

Правило формирования очереди (дисциплина очереди) – алгоритм постановки заявок в очередь – правила формирования очереди, в соответствии с которыми обслуживающий механизм принимает заявку к обслуживанию. Правила занятия каналов заявками и принятия заявок к обслуживанию в случае очереди: в порядке очереди, по минимальному времени получения отказа, в случайном порядке.

Три основных типа правил: бесприоритетное, приоритетное обслуживание, случайный отбор заявок. Возможные варианты: циклическое – по одному требованию из различных источников, возможность отказов от ожидания, выбытие требований из очереди по истечении определенного времени, зависимость приоритетов от времени или от длительности прогнозируемого обслуживания (первой обслуживается заявка, требующая наименьших затрат времени), от продолжительности ожидания, от внешних причин (дополнительной оплаты) и др.

Характеристики потока

Каждая СМО предназначена для обслуживания (выполнения) некоторого потока заявок (требований), поступающих на вход системы большей частью не регулярно, а в случайные моменты времени. Обслуживание заявок, в общем случае, также длится не постоянное, заранее известное время, а случайное время, которое зависит от многих случайных, порой неизвестных причин. После обслуживания заявки канал освобождается и готов к приему следующей заявки.

Рассмотрение процесса обслуживания отдельной заявки представляет лишь ограниченный интерес. Заявки образуют поток, последовательность поступления.

Источник – первопричина возникновения заявок независимо от их физической природы.

Основной фактор, определяющий протекающие в системе массового обслуживания процессы является поток заявок.

Примеры:

- поток вызовов на телефонной станции;

- поток включений приборов в бытовой электросети;

- поток грузовых составов, поступающих на железнодорожную станцию;

- поток неисправностей (сбоев) вычислительной машины;

- поток выстрелов, направляемых на цель, и т. д.

Входной поток – поток заявок на обслуживание системой.

Основные показатели описания входного потока: характеристики источника заявок, тип заявок, длина интервалов времени между поступлениями требований. Возможные варианты: групповые поступления заявок, ожидание вне системы, поступление заявок согласованными потоками, зависимость входного потока от состояния системы, поступления по графику, но с опозданиями и др. Поступление заявок зависит от внешних обстоятельств, и этот процесс описывается через случайные величины.

Поток событий (в данном случае заявок) - последовательность событий, наступающих одно за другим в какие-то заранее неизвестные, случайные моменты времени. Вид и параметры закона распределения входящего потока определяется характером физических процессов, протекающих в моделируемом объекте. Случайный характер потока заявок и длительности их обслуживания порождает в СМО случайный процесс.

Для решения задач оценки эффективности систем массового обслуживания необходимо этот случайный процесс изучить, т.е. построить и проанализировать его математическую модель.

На эти случайности, связанные с неоднородностью потока заявок, накладываются еще случайности, связанные с задержками обслуживания отдельных заявок. В силу случайного характера моментов поступления заявок процесс их обслуживания представляет собой случайный процесс. Построение математической модели такого процесса и изучение ее даст возможность оценить пропускную способность системы и дать рекомендации по рациональной организации обслуживания.

Такие модели используются при решении большого класса задач: проектирование систем обслуживания, автоматизация производства (ритмичность поступления деталей – потоки заявок к обслуживанию нарушается случайным образом), организация транспорта, сравнительная оценка эффективности систем различной структуры (среднее время простоя, среднее время безотказной работы и др.).

Входной поток заявок однозначно задается последовательностью моментов времени поступления заявок в систему t₁, t₂, . . . , t_k, . . ..

Чтобы описать случайный поток однородных событий как случайный процесс достаточно задать закон распределения, характеризующий последовательность случайных величин t₁, t₂, . . . t_k, Обычно вместо t₁, t₂, . . . t_k, . . задают случайные величины ξ₁, ξ₂, . . . , ξ_к, . . ., являющиеся длинами интервалов времени между последовательными моментами t_j:

t₁ = ξ₁,

t₂ = ξ₁ + ξ₂ ,

. . . . . . . .

t_к = ξ₁ + ξ₂ +. . . ξ_к._.

Для задания входного потока достаточно получить последовательность случайных величин ξ₁, ξ₂, . . , ξ_i, . . . с заданным законом распределения.

Выходной поток – поток заявок, покидающих систему.

Случайный процесс, протекающий в системе массового обслуживания, состоит в том, что система в случайные моменты времени переходит из одного состояния в другое: меняется число занятых каналов, число заявок в очереди.

Случайные процессы со счетным множеством состояний бывают двух типов: с дискретным временем (переход из состояния в состояние только в определенные, разделенные конечными интервалами, моменты времени) и с непрерывным временем (переход из состояния в состояние может осуществляться в любой момент времени).

В связи со случайностью потока заявок в системах массового обслуживания рассматриваются только процессы с непрерывным временем.

Для того чтобы описать случайный процесс в дискретной системе с непрерывным временем, необходимо проанализировать причины, вызывающие переход системы из состояние в состояние.

При рассмотрении процессов, протекающих в системе с дискретными состояниями и непрерывным временем, часто целесообразно представлять процесс так, как будто изменения состояний системы происходят под действием каких-то потоков событий (поток вызовов, поток неисправностей, поток заявок на обслуживание, поток посетителей и т. д.).

Если с точки зрения обслуживания все заявки потока оказываются равноправными и играет роль лишь сам факт наступления события, состоящего в появлении заявки, то такие потоки называются потоками однородных событий.

Для потока однородных событий получены аналитические решения оценки качества обслуживания.

Каждое событие однородного потока характеризуется моментом времени t_j, в который оно наступает. Поток событий, отличающихся только моментами появления, можно представить в виде последовательности точек t₁, t₂, . . . t_j, . .

Если однородный поток событий является детерминированным, то последовательность событий задается перечислением моментов времени наступления события или зависимостью, позволяющее определить текущее значение t_j по предыдущим.

Поток событий называется регулярным, если события следуют одно за другим через строго определенные промежутки времени.

Для решения многих прикладных задач можно ограничиваться частными случаями потоков.

Простейший поток событий (поток Пуассона) удовлетворяет трем условиям: он стационарен, ординарен и не имеет последействий.

Стационарный поток событий – вероятностные характеристики не зависят от времени - вероятность наступления заданного числа событий в течение интервала времени фиксированной длины зависит только от продолжительности этого интервала, но не зависит от его расположения на временной оси.

Стационарность потока означает его однородность по времени; вероятностные характеристики такого потока не меняются в зависимости от времени.

Для стационарного потока характерна постоянная плотность потока λ - среднее число событий в единицу времени. Или: вероятность р_к (t, t₀) появления к событий за промежуток времени (t₀, t₀ +t) не зависит от t₀, а зависит только от t и к.

Это не значит, что фактическое число событий, появляющихся в единицу времени, постоянно, поток может иметь местные сгущения и разрежения. Важно, что для стационарного потока эти сгущения и разрежения не носят закономерного характера, а среднее число событий, попадающих на единичный участок времени, остается постоянным для всего рассматриваемого периода.

На практике все процессы стационарны только в определенные промежутки времени. Например, поток заявок на телефонной станции в течение суток не может считаться стационарным, но в течение определенного промежутка времени – может.

Ординарный поток – вероятность появления двух и более событий в течение элементарного интервала времени ∆t есть величина бесконечно малая по сравнению с вероятностью появления одного события на этом интервале.

Условие ординарности означает, что заявки поступают в систему поодиночке, а не парами, тройками и т.д.

Поток отказов элементов технических систем (восстанавливаемых элементов), например электрических сетей, можно представить как ординарный поток. Поток обстрелов, которому подвергается воздушная цель в зоне действия ракетной зенитной ПВО, является ординарным, если стрельба ведется одиночными ракетами, и неординарным, если стрельба ведется одновременно двумя или несколькими ракетами.

Если в неординарном потоке события происходят только парами, только тройками и т. д., то можно его рассматривать как ординарный «поток пар», «поток троек» и т. д. Если число событий, образующих «пакет» (группу одновременно приходящих событий), случайно, то тогда приходится наряду с потоком пакетов рассматривать случайную величину X — число событий в пакете, и математическая модель потока становится более сложной.

Поток без последействия: заявки поступают независимо друг от друга – случайные величины являются независимыми, т.е. отсутствует вероятностная зависимость последующего течения событий потока от предыдущего – для любых неперекрывающихся интервалов времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие.

Пример: последействие отсутствует для потока пассажиров в метро, поскольку отсутствует зависимость между причинами, вызвавшими приход каждого из пассажиров на станцию. Но как только эта зависимость появляется, условие отсутствия последействия нарушается. Например, поток пассажиров, покидающих станцию метро, уже не обладает свойством без последействия, так моменты выхода для пассажиров, прибывших одним поездом, зависимы между собой.

Если такая зависимость появляется, условие отсутствия последействия оказывается нарушенным.

Пример: поток грузовых поездов, идущих по железнодорожной ветке. Если по условиям безопасности они не могут следовать один за другим чаще, чем через интервал времени 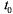, то между событиями в потоке имеется зависимость, и условие отсутствия последействия нарушается. Однако, если интервал 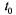мал по сравнению со средним интервалом между поездами, то такое нарушение несущественно.

Чаще всего выходные потоки заявок имеют последействие, даже если входной его не имеет. Последействие выходного потока необходимо учитывать, когда он является входным для другой системы (многофазное обслуживание, когда одна и та же заявка постепенно переходит из системы в систему).

При суперпозиции (взаимном наложении) достаточно большого числа потоков, обладающих последействием (лишь бы они были стационарны и ординарны), образуется суммарный поток, который можно считать простейшим, и тем точнее, чем большее число потоков суммируется. Дополнительно требуется, чтобы складываемые потоки были сравнимы по интенсивности, т. е., чтобы среди них не было, скажем, одного, превосходящего по интенсивности сумму всех остальных.

Если поток событий не имеет последействия, ординарен, но не стационарен, он называется нестационарным пуассоновским потоком. В таком потоке интенсивность λ (среднее число событий в единицу времени) зависит от времени: λ = λ(t), тогда как для простейшего потока λ=const.

Пуассоновский поток событий (как стационарный, так и нестационарный) тесно связан с известным распределением Пуассона — число событий потока, попадающих на любой участок, распределено по закону Пуассона.

Для простейшего потока (потока Пуассона) вероятность P_k (t) наступления k событий за интервал времени длины t выражается законом распределения Пуассона (вероятность того, что за время t произойдет к событий) - поэтому часто простейший поток называют пуассоновским потоком:

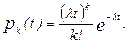
с математическим ожиданием a = λt.

Здесь λ – плотность потока (количество заявок в единицу времени).

Введем состояние системы следующим образом: система находится в состоянии Е_s в момент времени t, если к этому моменту в систему поступило s заявок. Вероятность того, что в момент времени t + ∆t система останется в том же состоянии, т.е. что за интервал времени ∆t в систему не поступит ни одной заявки:

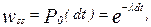S = 0, 1, 2, …,

разлагая в ряд, имеем w_ss = 1 – λdt.

Вероятность поступления в систему хотя бы одной заявки w_ss+1 = λdt.

Такой закон распределения называется показательным (или экспоненциальным). Величина 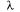называется параметром показательного закона. Ввиду стационарности потока полученные соотношения имеют то же значение и для любого другого момента времени.

Поскольку поток простейший (без последействия), наличие события в начале интервала t не влияет на появление события в дальнейшем.

Матрица переходов для простейшего потока и соответствующий граф

Матрица переходов   Е0 Е1 Е2 Е3 . . . Е0 1 – λdt λdt     . . . Е1   1 – λdt λdt   . . . Е2     1 – λdt λdt . . . Е3       1 – λdt . . . . . . . . . . . . . . . . . . . .

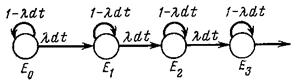
Случайный процесс, протекающий в СМО, называется марковским (или процессам без последействия, или процессом без памяти), если вероятность любого состояния СМО в будущем зависит только от ее состояния в настоящем и не зависит от ее состояний в прошлом.

Чтобы случайный процесс был марковским, необходимо и достаточно, чтобы все потоки событий, под воздействием которых происходят переходы системы из состояния в состояние, были пуассоновскими. Поток событий, обладающий свойствами отсутствия последействия (для любых двух непересекающихся промежутков времени, число событий, наступающих за один из них, не зависит от числа событий, наступающий за другой) и ординарностью (вероятность наступления за элементарный - малый промежуток времени более одного события пренебрежимо мала по сравнению с вероятностью наступления за этот промежуток времени одного события), называется пуассоновским.

В СМО потоками событий являются потоки заявок, потоки "обслуживании" заявок и т. д. Если СМО такова, что хотя бы один из ее потоков не является пуассоновским, то характеристики ее эффективности все же могут быть приближенно оценены с помощью марковской теории массового обслуживания. При этом, чем сложнее СМО, чем больше в ней каналов обслуживания — тем точнее оказываются приближенные формулы, полученные при предположении выполнимости в СМО марковских условий.

Под марковской СМО будем понимать систему, в которой все потоки событий, переводящие ее из состояния в состояние, пуассоновские. Если хотя бы один из потоков не является пуассоновским, то СМО будет называться немарковской.

Например, в системах со строго выполняющимся расписанием, с ленточным конвейером и им подобным поток входящих заявок является регулярным и, следовательно, не является пуассоновским.

Классификация СМО

Модели СМО классифицируются по различным признакам.

По типу случайного процесса – марковский или немарковский.

По характеру источника заявок различают системы с конечным или бесконечным числом заявок. В случае конечного, обычно постоянного числа заявок, заявки после завершения обслуживания возвращаются в источник, где они пребывают в течение некоторого времени, затем вновь поступают в систему. Во втором случае источник генерирует бесконечное число заявок, и работа источника не зависит от работы обслуживающей системы. Системы с конечным числом заявок называются замкнутыми, с бесконечным – разомкнутыми.

По отсутствию или наличию возможности ожидания – системы с отказами (заявка, поступившая в момент, когда все обслуживающие приборы заняты, получает отказ, покидает систему и в дальнейшем процессе обслуживания не участвует) и системы с ожиданием (если все линии обслуживания заняты, заявка становится в очередь и ожидает, пока одна из линий не освободится).

Системы с ожиданием делятся на системы с неограниченным ожиданием (любая заявка рано или поздно будет обслужена) и системы с ограниченным ожиданием (накладываются ограничения на длину очереди, время пребывания в очереди, общее время пребывания в системе).

Для систем с отказами показателем качества системы обслуживания обычно считаются вероятность отказа, среднее число отказов за данный интервал времени и т.д. Для систем с ожиданием показателями качества обслуживания могут быть среднее время ожидания заявки, средняя длина очереди и т.д.

По числу линий обслуживания – одноканальные (одна линия) и многоканальные (несколько линий).

По количеству этапов обслуживания СМО делятся на однофазные и многофазные системы.

По правилу формирования очереди – с общей очередью (общий накопитель) и несколькими очередями (накопитель разделен на зоны).

Для общей очереди ограниченной длины возможные алгоритмы постановки заявок в очередь:

- "по кольцу" – последовательно в порядке поступления, при достижении ограничения запись продолжается с первой позиции,

- с поиском свободных мест – при отсутствии свободных мест заявка получает отказ,

- приоритетные правила – заявки неоднородны по значимости, при отсутствии свободного места в очереди, заявка поступает на место заявки с меньшим приоритетом.

По правилу обслуживания: бесприоритетное – "первым пришел – первым ушел", приоритетное - в соответствии с номером приоритета - "последним пришел – первым ушел", случайный отбор заявок.

По дисциплине обслуживания СМО подразделяют на три класса:

СМО с отказами (нулевым ожиданием или явными потерями), в которых заявка, поступившая на вход СМО в момент, когда все каналы заняты, получает "отказ" и покидает СМО ("пропадает"). Чтобы эта заявка все же была обслужена, она должна снова поступить на вход СМО и рассматриваться при этом как заявка, поступившая впервые. Примером СМО с отказами может служить работа АТС: если набранный телефонный номер (заявка, поступившая на вход) занят, то заявка получает отказ, и, чтобы дозвониться по этому номеру, следует его набрать еще раз (заявка поступает на вход как новая),

СМО с ожиданием (неограниченным ожиданием или очередью). В таких системах заявка, поступившая в момент занятости всех каналов, становится в очередь и ожидает освобождения канала, который примет ее к обслуживанию. Каждая заявка, поступившая на вход, в конце концов будет обслужена. Такие СМО часто встречаются в торговле, в сфере бытового и медицинского обслуживания, на предприятиях (например, обслуживание станков бригадой работников).

СМО смешанного типа (ограниченным ожиданием). Это такие системы, в которых на пребывание заявки в очереди накладываются некоторые ограничения.

Эти ограничения могут накладываться на длину очереди, т.е. максимально возможное число заявок, которые одновременно могут находиться в очереди.

В качестве примера такой системы можно привести мастерскую по ремонту автомобилей, имеющую ограниченную по размерам стоянку для неисправных машин, ожидающих ремонта.

Ограничения ожидания могут касаться времени пребывания заявки в очереди, по истечению которого она выходит из очереди и покидает систему, либо касаться общего времени пребывания заявки в СМО (т.е. суммарного времени пребывания заявки в очереди и под обслуживанием).

В СМО с ожиданием и в СМО смешанного типа применяются различные схемы обслуживания заявок из очереди. Обслуживание может быть упорядоченным, когда заявки из очереди обслуживаются в порядке их поступления в систему, и неупорядоченным, при котором заявки из очереди обслуживаются в случайном порядке. Иногда применяется обслуживание с приоритетом, когда некоторые заявки из очереди считаются приоритетными и поэтому обслуживаются в первую очередь.

По ограничению потока заявок СМО делятся на замкнутые и открытые (разомкнутые).

Если поток заявок ограничен и заявки, покинувшие систему, могут в нее возвращаться, то СМО является замкнутой, в противном случае — открытой. Классическим примером замкнутой СМО служит работа группы наладчиков в цеху. Станки являются источниками заявок на обслуживание, и их количество ограничено, наладчики — каналы обслуживания. После проведения ремонтных работ вышедший из строя станок снова становится источником заявок на обслуживание.

Оценка эффективности СМО

Каждая СМО в зависимости от своих параметров: характера потока заявок, числа каналов обслуживания и их производительности, а также от правил организации работы обладает определенной эффективностью функционирования (пропускной способностью), позволяющей ей более или менее успешно справляться с потоком заявок.

Необходимо оценить эффективность обслуживания потока заявок системой заданной структуры (количество линий обслуживания, производительность каждой линии).

Цель - выработка рекомендаций по рациональному построению СМО, рациональной организации их работы и регулированию потока заявок для обеспечения высокой эффективности функционирования СМО.

Для достижения этой цели устанавливаются зависимости эффективности функционирования СМО от ее организации (параметров): характера потока заявок, числа каналов и их производительности и правил работы СМО.

В качестве критерия эффективности системы обслуживания могут быть использованы различные величины и функции, например, вероятность обслуживания каждой из поступающих заявок, средняя доля обслуженных заявок, среднее время ожидания обслуживания, среднее время простоя каждого из каналов и системы в целом, пропускная способность системы и т.д. Численное значение каждого из этих требований в той или иной степени характеризует эффективность системы по удовлетворению потока поступающих требований – пропускную способность системы. Пропускная способность зависит не только от параметров системы, но и от характера потока заявок.

Функциональные возможности СМО определяются следующими основными факторами:

- характеристики входного потока (интенсивность поступления заявок, тип потока, закон распределения);

- продолжительность обслуживания (число и характеристики каналов);

- дисциплина очереди;

- вместимость блока ожидания.

Для оценки эффективности системы строятся модели различных комбинаций факторов.

Основные операционные характеристики, определяющие эффективность СМО:

- вероятность обслуживания заявки системой;

- пропускная способность системы - отношение среднего числа заявок, обслуживаемых СМО в единицу времени, к среднему числу поступивших заявок за это же время;

- вероятность отказа;

- вероятность занятости каждого из каналов и всех вместе каналов;

- вероятность простоя каждого из каналов и всех вместе каналов;

- среднее время занятости системы;

- среднее количество заявок в очереди;

- среднее время ожидания;

- среднее время обслуживания;

- коэффициент использования СМО - средняя доля времени, в течение которого СМО занята обслуживанием заявок, и т.п.

Определение показателей эффективности системы позволит выявить основные параметры системы и направления работ по повышению эффективности (что нужно сделать – увеличить количество каналов, пропускную способность каналов, количество мест в очереди и др.). Для этого оценивается чувствительность каждого показателя к изменению параметров системы.

Аналитические и статистические модели

Известны аналитические соотношения теории массового обслуживания, связывающие характеристики потока заявок и параметры системы с показателями качества обслуживания для простейшего (пуассоновского) потока, к которому могут быть сведены многие практические задачи.

Разработанные аналитические методы обычно относятся к моментам времени, достаточно удаленным от начала процесса – когда уже наступил стационарный режим.

Обобщение математической модели массового обслуживания идет по следующим направлениям.

Рассматривался однородный поток заявок, но на практике более распространены задачи, требующие учета имеющейся неоднородности заявок в потоке. Особенно это существенно тогда, когда параметры процесса обслуживания (например, его длительность, качество и др.) зависят не только от времени поступления заявки, но и от ее характеристик.

Примеры. При обработке детали на станке время обработки зависит от ее сложности, размеров, характеристик материала и т.п. При обработке потока самолетов в аэропорт помимо времени прибытия учитывается тип самолета, скорость, высота, курс, длина пробега и т.п.

В случае неоднородных заявок (для их описания необходимо привлекать другие параметры, кроме момента поступления в систему) применяется обобщенное понятие потока: каждая j-ая заявка характеризуется моментом поступления t_j и n параметрами а₁, а₂, . . . , а_n.

Другими словами, каждая заявка представляет собой (n + 1)-мерный вектор вида v_j = v (t_j, α_1j, α_2j, . . . , α_nj) в пространстве параметров t, α₁, α₂, . . . , α_n.

Часто приходится учитывать случайные отклонения от нормы не только моментов поступления, но и случайный характер параметров заявок (размеров, температуры, скорости, твердости, координат и др.). Поэтому в общем случае заявки описываются случайными векторами, и мы приходим к необходимости рассматривать случайные потоки векторов.

В рассмотренных системах параметры системы обслуживания предполагались независимыми от потока заявок.

При неоднородном потоке заявок параметры системы обслуживания (число каналов, характеристики закона распределения времен занятости канала, например, среднее время обслуживания) реально могут зависеть от характеристик потока заявок. Если считать поток заявок потоком случайных векторов, то параметры системы обслуживания могут быть функциями t_j и величин α_1j, α_2j, . . . , α_nj Например, длительность обработки детали может определяться ее размерами, твердостью материала, температурой и др.

Аналитические математические модели могут быть построены для каждого типа системы с простейшим потоком заявок (с ожиданием, без ожидания и др.).

Аналитические методы анализа систем массового обслуживания пригодны для получения качественных характеристик и практически могут использоваться для сравнительно простых случаев.

Реальные входные потоки по своим свойствам далеко не всегда соответствуют простейшему потоку, время обслуживания часто распределяется не по показательному закону, дисциплина обслуживания может быть достаточно сложной.

На практике приходится сталкиваться с многофазными системами. Системы массового обслуживания, составляющие различные фазы обслуживания, могут быть неодинаковыми, и характер операций, обслуживания на различных фазах, может быть различным. На последующих фазах могут появиться заявки, которые не поступали на предыдущие фазы, может оказаться, что обслуживание, относящееся к последующей фазе, начинается еще до окончания обслуживания еще на предыдущей фазе и т.д.

Порядок использования свободных линий (каналов) и порядок выбора заявок из очереди может не устанавливаться заранее, и в процессе обслуживания заявок изменяться и не зависеть от характеристик потока заявок.

В реальных процессах, которые могут быть представлены как системы массового обслуживания (например, в процессах с управлением), может содержаться элемент, способный определять оптимальный порядок обслуживания.

Для математического описания процессов с управлением удобно использовать такие системы массового обслуживания, которые снабжены специальным алгоритмом, позволяющим по известным данным о заявках и состояниях обслуживающих средств определить порядок обслуживания, и, возможно, целесообразное изменение структуры самой системы. Пример такой системы массового обслуживания – моделирование дискретных производственных процессов.

Для анализа стохастических систем, когда аналитическое описание процесса получить затруднительно, используется метод статистического моделирования (имитационного моделирования).

Вместо того, чтобы описывать случайное явление аналитически, производится его моделирование с помощью некоторой процедуры, дающей случайный результат. С помощью специальных моделирующих алгоритмов формируются реализации потока заявок с заданным законом распределения интервалов между заявками. Здесь самое главное – определить вид закона распределения.

9.2 Модели дискретного производственного процесса

При моделировании дискретного производственного процесса он расчленяется на отдельные акты – производственные операции.

Между производственной операцией и формализованной операцией не всегда однозначное соответствие – данная реальная элементарная производственная операция для формализации может быть достаточно сложной, тогда ее описывают с помощью совокупности нескольких формализованных операций. В общем виде расчленение производственного процесса на элементарные акты не решается – это делается в зависимости от конкретных обстоятельств.

Строится математическое описание каждого элементарного акта и взаимодействия между ними, характеризующего совокупность элементарных актов как единый процесс.

Типичные абстрактные операции, соответствующие достаточно широкому классу производственных операций: операции обработки, сборки и управления.

Выполнение производственной операции над системой (изделием, полуфабрикатом) обязательно связано с изменением ее свойств, описываемых числовыми характеристиками или параметрами, т.е. выполнение операции связано с изменением значений параметров системы.

Каждая производственная операция может быть представлена как оператор, определяющий изменение фазовых координат (значений параметров) системы во времени. Тогда математическая модель производственной операции может быть представлена как модель динамической системы (детерминированная или стохастическая), а модель производственного процесса - как многоуровневая динамическая модель.

Математическое описание элементов производственного процесса основано на наборе параметров, характеризующих систему (полуфабрикаты, заготовки, детали, узлы и т.д.). В дальнейшем объект, над которым совершается производственная операция, будем называть полуфабрикатом.

Среди характеристик полуфабрикатов различаются координаты состояния (изменяются по ходу производственного процесса в результате производственных операций) и фиксированные параметры (в рамках данного производственного процесса).

Сущность формализации операции состоит в переработке информации, описывающей состояния участвующих в операции полуфабрикатов.

Моделируется процесс производственной операции (обработки, сборки) как процесс переработки информации о полуфабрикатах и процесс функционирования сборочного оборудования (учитывает синхронизацию операций и влияние возмущающих факторов).

Большинство дискретных производственных процессов могут быть описаны как системы массового обслуживания и исследованы методами имитационного моделирования по принципу особых состояний («по ∆z»).

Для систем массового обслуживания особые состояния появляются в моменты поступления новых заявок или в моменты окончания обслуживания и освобождения каналов (количество свободных каналов или заявок в очереди меняется скачком).

Свойства таких систем оцениваются по информации об особых состояниях, неособые состояния для оценки свойств систем интереса не представляют.

Примером имитационной модели является график движения поездов, где наглядно указаны моменты прибытия и отправления поездов, периоды следования поездов по перегонам, периоды ожидания и пропуска встречных поездов. На компьютер возлагается как работа по воспроизведению процесса функционирования имитационной модели, так и по проведению экспериментов с ней.

Типичные прикладные задачи, которые решаются методом имитационного моделирования: определение оптимальных заделов деталей и полуфабрикатов, оценка оптимальных объемов карманов и местных складов, определение узких мест, ограничивающих производительность оборудования, и другие.

Операции обработки

Абстрактная операция обработки – такой элементарный акт производственного процесса над полуфабрикатом, в результате которого меняется хотя бы одна из координат состояния полуфабриката.

Реальные технологические операции обработки: изменения размеров полуфабриката (обработка резанием, ковка, штамповка и т.д.), положения в пространстве (транспортировка, повороты), сообщение полуфабрикату дополнительного признака (окрашен, проверен) и т.д.

В качестве операции обработки могут быть формально представлены некоторые естественные акты производственного процесса, обычно не относящиеся к операциям, например, остывание (заготовки из печи), высыхание, окисление.

Под операцией обработки можно также понимать любые объединения последовательных подобных актов, особенно если они относятся к одному оборудованию.

Каждая операция обработки выполняется вполне определенным формализованным станком, обеспечивающим выполнение операции обработки (независимо от его реальной структуры и назначения).

Станок - любой комплекс производственного оборудования.

Математическое описание операции обработки - установление соотношений между параметрами, характеризующими взаимодействие станка и полуфабрикат

Дата добавления: 2014-08-04; просмотров: 649; Нарушение авторских прав

Мы поможем в написании ваших работ!