СМО с потерями заявок (полнодоступный пучок)

В полнодоступном пучке обслуживающих приборов любой вход может быть связан с любым свободным выходом. Характерным примером полнодоступного пучка служит так называемый "квадратный" коммутатор, в котором любой вход может быть соединен с любым выходом.

Рассмотри полнодоступный пучок, состоящий из исправных линий. Пусть на него поступает нагрузка с интенсивностью 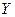. Вероятность занятости ровно 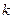линий – определяется по такой формуле:

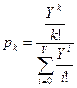. (1)

Очевидно, что сумма всех вероятностей равна единице. Набор вероятностей { } называют усеченным распределением Пуассона. При 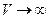распределение (1) становится пуассоновским.

Вероятность определяет то состояние СМО, когда все линии заняты. Она используется как оценка вероятности потерь заявок. Ее обозначают разными символами:

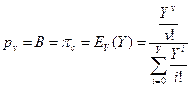. (2)

Формула (2) была выведена Эрлангом. Иногда ее называют B-формулой Эрланга или первой формулой Эрланга. Есть и другие названия. Для вывода формулы (2) Эрлангом использовались предположения о пуассоновском входящем потоке и экспоненциальном распределении длительности обслуживания заявок. Позже Б.А. Севастьянов доказал, что соотношение, полученное А.К. Эрлангом, справедливо для любого закона распределения длительности обслуживания заявок.

Для рассматриваемой формулы Эрланга справедливо рекуррентное соотношение следующего вида:

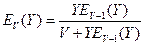. (3)

Это соотношение очень полезно для минимизации ошибки вычислений вероятности потерь. Формула Эрланга табулирована. Практически все учебники содержат таблицы, которые позволяют вычислять одну из переменных в формуле (2). В подобных таблицах переменные меняются дискретно. Для емкости пучка это естественно. Для других величин (вероятность потерь и нагрузка) не всегда приемлема подобная форма представления данных.

Существует также ряд так называемых калькуляторов Эрланга. Это очень простые программы, обычно работающие под операционной системой Windows. Они позволяют быстро вычислять любую из величин, входящих в формулу (2), по двум заданным аргументам. Калькуляторы Эрланга можно найти в Internet.

Распределение числа занятых линий в пятилинейном пучке СЛ приведено ниже для трех значения интенсивности нагрузки.

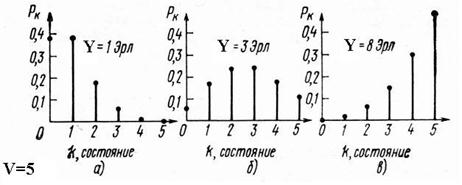
Зависимость вероятности потерь от интенсивности поступающей нагрузки показана для нескольких значений количества линий .

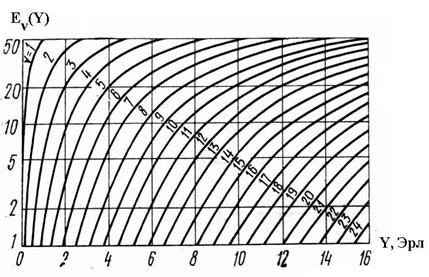
Зависимость интенсивности поступающей нагрузки от вероятности потерь и емкости пучка СЛ показана при помощи двух графиков.

В первых автоматических системах коммутации использовался исключительно алгоритм обслуживания заявок с потерями. В следующих поколениях коммутационной техники стали применяться различные виды алгоритмов с ожиданием. Тем не менее, для пучков СЛ чаще всего используется алгоритм обслуживания с потерями. Если свободной СЛ нет, то вызов теряется. Такой способ обслуживания иногда называют алгоритмом с явными потерями. Принято различать три вида явных потерь и соответствующие вероятности:

· потери по вызовам – ;

· потери по нагрузке – ;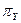

· потери по времени – .

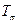Вероятность за период времени определяется отношением числа потерянных вызовов к их общему числу. Вероятность 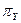за тот же период времени 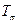вычисляется аналогично. Только необходимо делить величины потерянной и поступающей нагрузки. Потери по времени за период 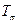– та его часть, когда все поступающие вызовы будут потеряны из-за отсутствия ресурсов для обслуживания трафика. Эту часть периода 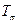называют также опасным временем. Для полнодоступного пучка, обслуживающего пуассоновский поток первого рода, справедливо тождество:

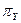= = . (4)

Для анализа СМО с потерями часто необходимо определить среднее число занятых линий 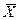в пучке емкостью , который обслуживает нагрузку с интенсивностью 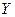. Эта величина определяется следующим образом:

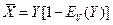. (5)

Естественно, что число занятых линий в пучке емкостью – случайная величина. Поэтому целесообразно оценить ее дисперсию – 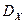. Она вычисляется по такой формуле:

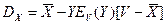. (6)

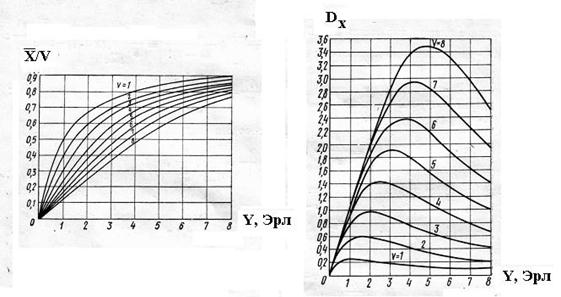
Зависимость величин 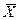и 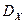от интенсивности поступающей нагрузки приведена на двух графиках.

Для случая 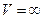справедливо такое соотношение: = = .

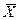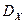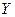Первый график свидетельствует, что обслуженная нагрузка в расчете на одну линию растет по мере увеличения емкости пучка . Это явление объясняется природой трафика.

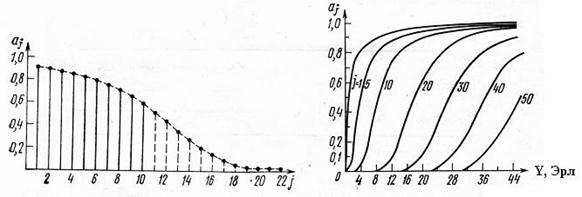
Для решения ряда задач необходимо знать интенсивность нагрузки, обслуженной 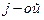линией полнодоступного пучка, – 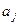. Соответствующий график показывает, что лучше используются линии с меньшим значением .

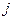Формула (2) определена для целых значений . В некоторых случаях интересны дробные значения . Тогда использует выражение, содержащее гамма-функцию, которая для целых значений определяется факториалом: 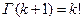Кроме того, формула (2) может использоваться для расчета вероятности потерь в СМО при поступлении потока, являющегося неординарным. Соответствующие формулы громоздки и приводятся редко.

Для пуассоновского потока второго рода, который генерируется конечным числом источников трафика, справедлива формула Энгсета. Речь идет о примитивном потоке с параметром 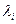. Длительность обслуживания заявок в СМО предполагается случайной с экспоненциальным распределением. Параметр примитивного потока определяется числом источников нагрузки ( ) и параметром потока вызовов свободного источника ( ):

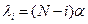. (7)

Введем единый параметр интенсивности нагрузки:

. (8)

С учетом принятых обозначений вероятность потери вызова можно представить следующим образом:

. (9)

Данное выражение представляет собой формулу Энгсета для вероятности потерь по вызовам. Тождество = = 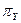для пуассоновского потока второго рода нельзя считать верным. Для расчета вероятности потерь по времени справедлива такая формула:

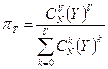. (10)

Очевидно, что 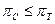. Этим СМО с входящим пуассоновским потоком второго рода отличаются от тех систем, для которых справедливо тождество = = 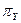. Потери по нагрузке определяются по такой формуле:

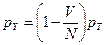. (11)

Очевидно, что при и 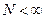справедливо неравенство .

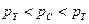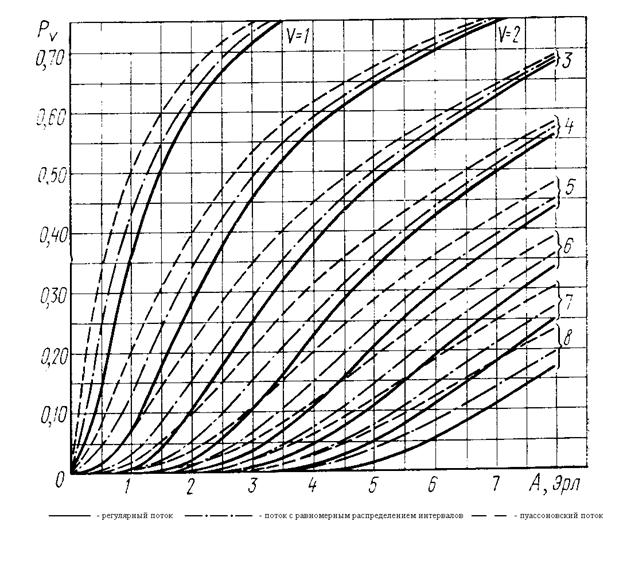
Вероятность потерь для регулярного потока, потока с равномерным распределением A(t) и пуассоновского потока, иллюстрируется при помощи семейства кривых для разных значений количества линий .

Дата добавления: 2014-08-09; просмотров: 424; Нарушение авторских прав

Мы поможем в написании ваших работ!