Главная страница Случайная лекция
Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика
Мы поможем в написании ваших работ!
А другой непроецирующий
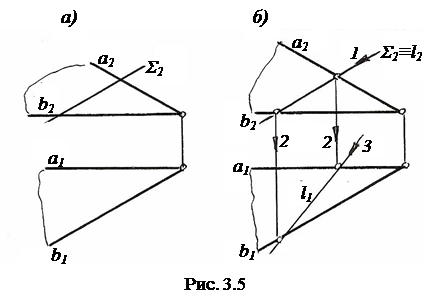
3.2.1. Построение линии пересечения двух плоскостей. На рис. 3.5, а заданы Τ (а∩b) – плоскость общего положения, и Σ – фронтально-проецирующая плоскость. Фронтальная проекция линии пересечения плоскостей ℓ (ℓ2) совпадает со следом плоскости Σ (Σ2), т. е. Σ2≡ℓ2. Горизонтальную проекцию линии ℓ (ℓ1) находим по принадлежности линии ℓ плоскости Τ (рис. 3.5, б)
3.2.2. Линии пересечения конической поверхности с плоскостями.Прямой круговой конус имеет пять видов линий пересечения в зависимости от положения секущей плоскости по отношению к оси конуса.
Обозначим угол между образующей конуса и его осью буквой φ, а угол между секущей плоскостью и осью конуса буквой α (рис. 3.6).
Возможны следующие виды линий пересечения:
1) если α=90°, то плоскость P пересекает поверхность по окружности;
2) если 90°>α>φ, то плоскость Σ пересекает поверхность по эллипсу;
3) если α=φ, т. е. секущая плоскость Τ параллельна одной образующей, то поверхность пересекается по параболе;
4) если 0≤α<φ, т. е. секущая плоскость Ψ параллельна двум образующим, то поверхность пересекается по гиперболе;
5) если 0≤ α<φ и секущая плоскость Ω проходит через вершину конуса, то поверхность пересекается по двум образующим.
3.2.3. Построение проекций и натуральной величины линии пересечения конической поверхности с плоскостью.На рис. 3.7 заданы коническая поверхность и фронтально-проецирую-щая плоскость Т. В данном случае при пересечении получается парабола. Так как плоскость Τ┴Π2 , то фронтальная проекция параболы совпадает с Τ2.
Для того, чтобы построить горизонтальную проекцию параболы, на её фронтальной проекции отмечаем ряд точек 12,…,72. Горизонтальные проекции точек 11,…,71 строим с помощью параллелей.
Натуральную величину параболы строим по точкам с помощью введения дополнительной плоскости проекций Π5||Τ. Так как парабола является симметричной фигурой, то для удобства построений ось х12 взята совпадающей с осью симметрии горизонтальной проекции конуса. Ось х25||Τ2. Построение видно из чертежа.
3.2.4. Построение проекций и натуральной величины линии пересечения сферы с плоскостью.При пересечении сферы с любой плоскостью образуется окружность.
На рис. 3.8 сфера пересекается горизонтально-проецирующей плоскостью Σ. Окружность, получаемая при пересечении плоскости Σ со сферой, при проецировании на Π1 совпадает со следом плоскости Σ (Σ1) – это отрезок 11-21. На фронтальную плоскость Π2 окружность проецируется в виде эллипса, причём 12-22 – малая ось эллипса, 32-42 – большая ось эллипса. Промежуточные точки можно построить с помощью параллелей.
Натуральная величина окружности построена с помощью введения дополнительной плоскости проекций Π4||Σ. Ось х14 проводим параллельно Σ1.
Построение видно из чертежа.
3.2.5. Построение проекций линии пересечения конуса и призмы.Нарис. 3.9 заданы конус и призма. В данном случае три грани призмы перпендикулярны Π2, поэтому фронтальная проекция линии пересечения совпадает с фронтальной проекцией призмы 12-32-52.
Горизонтальная проекция линии пересечения построена по принадлежности конусу с помощью параллелей.
Таким образом, когда один из пересекающихся геометрических объектов проецирующий, а другой непроецирующий, то одна из проекций линии пересечения на чертеже уже определена, а другая проекция определяется по принадлежности непроецирующему геометрическому объекту.
| <== предыдущая страница | | | следующая страница ==> |
| Оба геометрических объекта проецирующие | | | Оба геометрических объекта – непроецирующие |
Дата добавления: 2014-09-26; просмотров: 700; Нарушение авторских прав
Мы поможем в написании ваших работ!