Т-критерий

Т- критерий служит для сравнения двух средних значений из нормального распределения генеральных совокупностей х, у. В предположении, что среднеквадратичное отклонение 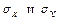равны хотя и неизвестны. Таким образом проверяется гипотеза 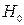утверждающая, что M[x]=M[Y]. Пусть 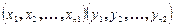две независимые случайные выборки из обеих генеральных совокупностей Х и У они могут иметь различные объемы, в качестве контрольной используют величину

(10.2)

В качестве контрольной используют величину (10.2), при сделанных предположениях ( о нормальном распределении совокупностей Х,У) и о равенстве дисперсий в предположении, что гипотеза 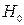- правильная Т удовлетворяет t- распределению Стьюдента с параметром 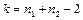- число степеней свободы. Поэтому, критическая область В критерии может быть установлено следующим образом: для уровня значимости 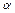из таблицы для Т-распределения. Определим значение t по 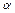и по параметру 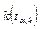. Если вычисление согласно (10.2) рассчитанный параметр t удовлетворяет неравенству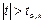

то гипотезу отвергают, по отношению к предпосылке нормальной распределенности. Т- критерий не очень чувствителен, его можно применять , если статистическое распределение обеих выборок не слишком асимметричны

Пример: нужно проверить влияние различных нормальных смесей на увеличение веса животных.

Для этого 10 животных кормили смесью №1, а 10 других - смесью №2. Пусть Х это увеличение массы при одной кормовой смеси, У - при другой. Величины Х и У можно считать нормально распределенными, т.к. дисперсия увеличения массы складывающаяся из свойства отдельных животных. А эти свойства не зависят от питания, то можно принять 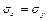, таким образом выполняются предпосылки для применения t- критерия. Имеем следующие эмпирические средние значения 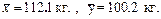Эмпирические дисперсии равны соответственно 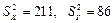. По (10.2) получаем

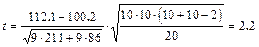
Для доверительной вероятности 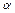=0.05 и k=18 из таблицы для t- критерия находим 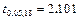. Так как 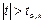, то гипотеза 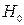отвернута. Отсюда следует, что с вероятностью порядка 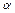=0.05 следовательно можно сказать, что один корм лучше другого.

Дата добавления: 2014-02-26; просмотров: 558; Нарушение авторских прав

Мы поможем в написании ваших работ!