
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Описание МНК (метод наименьших квадратов)
Метод наименьших квадратов - один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки
Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений.
Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.
В большинстве экспериментальных данных, задаваемых с помощью табличной функции, имеется достаточно большой разброс точек. При этом использование кусочной или непрерывной интерполяции не всегда оправдано, поскольку ставится задача исследовать общую тенденцию изменения физической величины.
В этом общем случае аппроксимации искомая кривая не обязательно должна проходить через заданные точки.
Рассмотрим рис. 1, отражающий большой разброс точек. В простейшем случае будем искать аппроксимирующую функцию ф(х) в виде полинома первой степени (прямой):
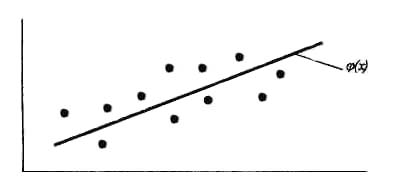
Рис. 2. График аппроксимации
Таким образом, данная система точек группируется вокруг искомой прямой. Эту прямую легко провести на глаз так, чтобы она наиболее близко подходила к исходным точкам. Однако можно найти уравнение прямой более строгими математическими методами.
Метод наименьших квадратов наиболее часто используют для решения контрольных по эконометрике для нахождения параметров уравнений (линий, степенной функции, гиперболы и т.д.)
Пусть общее количество точек равно n. Отклонение i-й точки от искомой прямой:
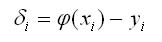
видно из рис. 2, отклонения могут быть как положительными, так и отрицательными. Поэтому для того, чтобы определить близость искомой функции к табличным точкам, необходимо составить сумму квадратов всех отклонений.
Метод наименьших квадратов заключается в минимизации суммы квадратов отклонений. В нашем случае эта функция равна
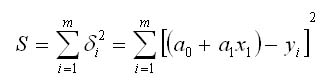
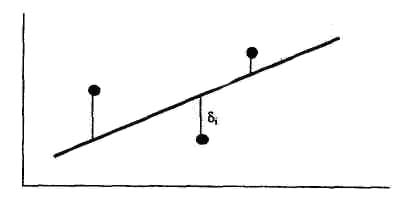
Рис. 2. График отклонения
Для нахождения минимума функции S необходимо приравнять нулю ее частные производные. В результате получим систему уравнений:
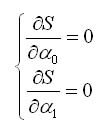
Опуская промежуточные преобразования, получим систему уравнений для нахождения неизвестных коэффициентов:
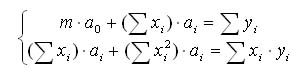
Здесь m - количество точек; суммирование здесь и далее предполагается по всем точкам.
Метод наименьших квадратов несложно распространить на общий случай, когда мы будем искать функцию ф(х) в виде полинома степени n:
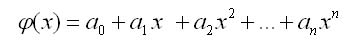
Отметим, что в случае аппроксимации всегда справедливо следующее соотношение, связывающее количество исходных точек m и степень искомого полинома:
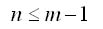
причем в случае равенства мы приходим к интерполяции (все отклонения равны нулю).
Неизвестные коэффициенты, а находим из условия минимизации суммы квадратов отклонений искомой функции от исходных точек. По аналогии с полиномом первой степени в нашем случае имеем систему уравнений: Z*A = B где Z - квадратная матрица размерностью (n+1)х(n+1), составленная из известных координат точек, А - вектор неизвестных коэффициентов; Y- вектор-столбец свободных членов.
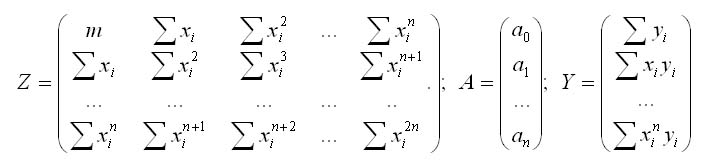
| <== предыдущая страница | | | следующая страница ==> |
| Mathcad | | | Постановка задачи. Для полного массива исходных данных с помощью персонального компьютера в системе MathCAD |
Дата добавления: 2014-09-29; просмотров: 857; Нарушение авторских прав

Мы поможем в написании ваших работ!