ЭЛЕКТРОТЕПЛОВАЯ АНАЛОГИЯ

Теплопроводность в твердых телах без внутренних источников теплоты описывается дифференциальным уравнением теплопроводности:

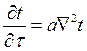, (5.1)

где 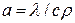– коэффициент температуропроводности, м²/с; 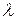–теплопроводность, Вт/(м·К); с – теплоемкость, Дж/(кг·К); 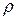– плотность, кг/м³; 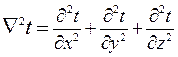– оператор Лапласа.

При стационарном процессе 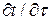=0, тогда: 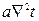=0. Но физическая характеристика тела 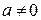, следовательно 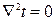, или:

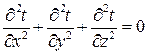. (5.2)

Пусть однородное и изотропное тело бесконечно вдоль оси z (рис. 5.1). Тогда температура вдоль оси z не изменяется и распределение электрических потенциалов и температур описываются уравнениями Лапласа:

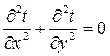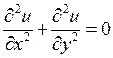; (5.3)

и граничными условиями:

• на нижних поверхностях ; ;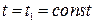

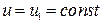• на верхних поверхностях ; .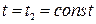

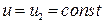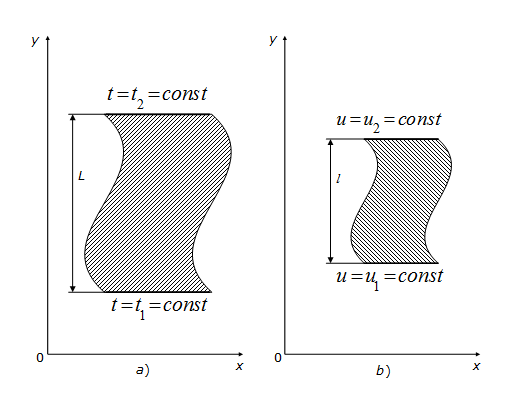
Рис. 5.1. а) изучаемое тело; b) лист электропроводящей бумаги

Итак, процессы электропроводности и теплопроводности описываются одинаковыми по форме уравнениями (5.3), то есть имеет место так называемая электротепловая аналогия (ЭТА).

Приведем уравнения (5.3) и граничные условия к безразмерному виду, выбрав в качестве масштабов отнесения L и l для координат; 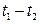и 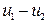для падений температур и потенциалов. Тогда по условиям геометрического подобия тел «a» и «b» безразмерные координаты сходственных точек будут одинаковыми:

; ,

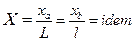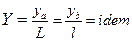а безразмерные падения температур и потенциалов:

; .

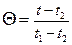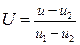Итак, безразмерные уравнения Лапласа:

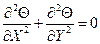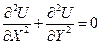; (5.4)

и граничные условия:

• на нижних поверхностях 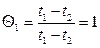; ; 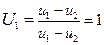(5.5)

• на верхних поверхностях 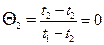; 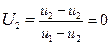. (5.6)

Следовательно, тождественность граничных условий первого рода:

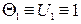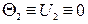; (5.7)

и решения уравнений Лапласа (5.4) при граничных условиях (5.7) будут тождественно одинаковы для сходственных точек тела и его электрической модели:

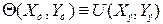. (5.8)

Итак, температуры t по измеренным значениям потенциалов u в различных точках модели определяются из соотношения:

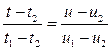. (5.9)

Исходя из закона Фурье для теплопроводности тепловой поток через поперечное сечение тела 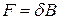, Вт:

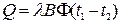, (5.10)

где В – длина тела, м; 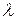– теплопроводность тела, Вт/(м·К); 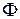– коэффициент формы.

По закону Ома ток через лист электропроводящей бумаги толщиной 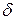, А:

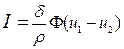. (5.11)

Здесь 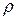– удельное электрическое сопротивление листа электропроводящей бумаги; 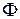– коэффициент формы.

Вследствие тождественности полей температур 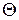в исследуемом теле и полей потенциалов U (5.8), коэффициенты формы в уравнениях (5.10) и (5.11) численно равны.

Если известно 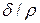, то из формулы (5.11) можно найти коэффициент формы 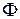, подставить его в уравнение (5.10) и с учетом выражения (5.9) найти тепловой поток через исследуемое тело.

Метод электротепловой аналогии (ЭТА) позволяет заменить измерение температур и тепловых потоков в исследуемом теле измерением электрических величин в модели. Они определяются проще и точнее по сравнению с тепловыми величинами на реальном теле.

Дата добавления: 2014-09-29; просмотров: 715; Нарушение авторских прав

Мы поможем в написании ваших работ!