
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Формулировка граничных условий для функции напряжений. Рамная аналогия профессора Папковича
Для определения функции напряжений и ее нормальной производной на контуре (производной по перпендикуляру к контуру) упругого тела необходимо взять раму, имеющую очертания контура тела, выбрать в этой раме статически определимую основную систему, загрузить ее внешними нагрузками, действующими на упругое тело. Тогда функция напряжений на контуре тела будет совпадать со значениями эпюры моментов, построенной для основной системы. Нормальная производная будет совпадать со значениями эпюры продольных сил. То есть
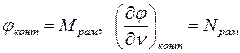
Правило знаков рамной аналогии.Эпюра изгибающих моментов строится со стороны растянутого волокна и считается положительной на тех участках, где она расположена внутри контура. Эпюра продольных сил считается положительной там, где продольная сила растягивает.
| <== предыдущая страница | | | следующая страница ==> |
| Уравнение совместности деформаций, выраженное через функцию напряжений | | | Доказательство рамной аналогии |
Дата добавления: 2014-07-19; просмотров: 350; Нарушение авторских прав

Мы поможем в написании ваших работ!