Доказательство рамной аналогии

Рассмотрим контур тела, загруженный так же как и упругое плоское тело (Рис.7).

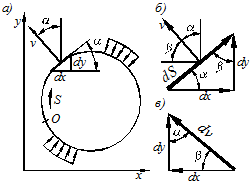
Пусть на контуре точка «О» является точкой начала отсчета дуг. Рассмотрим малый элемент дуги 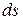,соответствующий приращениям координат 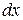и 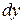. Направляющие косинусы внешней нормали к выделенному элементу равны

,

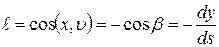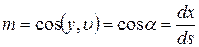
Сведения из математики. Есл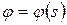и и 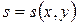, то производная функции зависящей от параметра вычисляется следующим образом

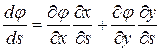
Выразим составляющие внешней нагрузки через функцию напряжений на контуре

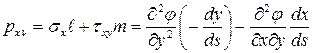
Эту зависимость можно переписать в следующем виде

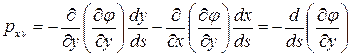
Подобным же образом можно показать, что

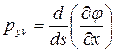
Если взять интегралы от компонент распределенной нагрузки с пределами от начала отсчета дуг до текущего значения дуги 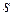, то получим равнодействующие нагрузки, действующие в сечении 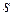контура

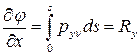
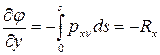
Производные от функции напряжений на контуре упругого тела равны равнодействующим внешних нагрузок по осям 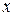и 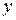. Выясним смысл производных от функции напряжений по длине дуги и по нормали к контуру. По определению производной и с учетом двух последних зависимостей имеем

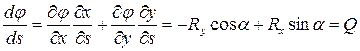
На рисунке 8-а видно, что полученная сумма представляет собою поперечную силу в контуре рамы в сечении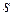

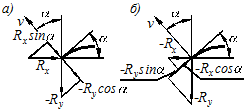
Рисунок 8

Производная функции напряжений по нормали к контуру выражается также через равнодействующие внешней нагрузки. Из рисунка 7-в видно, что и 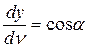. Тогда по определению имеем

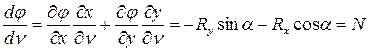
Две проекции равнодействующих внешних нагрузок на касательную к контуру представляют собой продольную силу в раме, имеющей очертание контура упругого тела.

Для определения функции напряжений на контуре проинтегрируем выражение производной

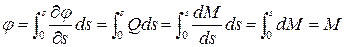
Рамная аналогия доказана.

ЛИТЕРАТУРА

1. Безухов Н.И. Основы теории упругости, пластичности и ползучести: Учебник для студ. втузов. – М.: Высш.шк., 1968. – 512с.

2. Безухов Н.И., Лужин О.В. Приложение методов теории упругости к решению инженерных задач: Учеб. пособие для втузов. – М.: Высш.шк., 1974. – 200с.

3. Прочность, устойчивость, колебания. Справочник в трех томах. Том 1. / Под ред. И.А. Биргера и Я.Г. Пановко. – М.: Машиностроение, 1968. – 812с.

4. Короткова С.Е. Механика клеевых соединений. – Алчевск: ДГМИ, 1998. – 187 с.

5. Короткова С.Е. Особенности постановки задачи концентрации напряжений в клеевом соединении с жестким швом дифференциально – разностным методом // Сопротивление материалов и теория сооружений. Вып. 67. – Киев: КНУБА, 2000. – С.104-110.

6. Короткова С.Е. Сочетание метода сил с дифференциально – разностным методом при расчете клеевых соединений // Строительные конструкции. Вып. 49. – Киев: НИИСК, 1998. – С.81-90.

7. Варвак П.М. Развитие и приложение метода сеток к расчету пластинок. Некоторые задачи прикладной теории упругости в конечных разностях. – Киев: Наук. Думка, 1952. – 330с.

8. Длугач М.И. Метод сеток в смешанной плоской задаче теории упругости. – Киев: Наук. Думка, 1964. – 260с.

9. Валишвили Н.В. Методы расчета оболочек вращения на ЭЦВМ. // Библиотека расчетчика.– М.: Машиностроение, 1976. – 278с.

Дата добавления: 2014-07-19; просмотров: 461; Нарушение авторских прав

Мы поможем в написании ваших работ!