Доказательство противоречием

Доказательство теоремы 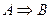называется синтетическим, если оно проводится по следующей логической схеме

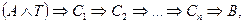
где Т – определенная совокупность утверждений той математической теории в рамках которой и происходит доказательство данного предложения и которой принадлежит конечная последовательность предложений С₁, С₂, …, С_n, составляющих доказательство, а также суждения А и В.

Значит, доказательство теоремы 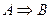синтетическим методом начинается с получения некоторого следствия С₁ из условия теоремы А, или части условия теоремы и положений теории Т, истинность которых известна. Затем аналогично получают следующее следствие С₂ и т.д. до тех пор, пока из последнего полученного следствия С_n легко получаем вывод заключения теоремы В.

Данный способ доказательства обладает как недостатками, так и достоинствами. К недостаткам следует отнести большую степень неопределенности в процессе проведения доказательства, что порождает у школьников чувство искусственности при проведении такого доказательства. Даже если школьники и слушают излагаемое учителем синтетическое доказательство, то для них мотивы предпринимаемых шагов остаются, как правило, скрытыми до завершения доказательства. Это обстоятельство и затрудняет обучение доказательству теорем школьников синтетическим методом. Им непонятно, почему берется именно эта, а не какая-то другая часть условия теоремы; почему вводятся в доказательство именно эти дополнительные предложения и понятия; почему выводится именно это следствие на данном этапе, а не другое. И только в конце доказательства все становится на свои места.

К достоинствам следует отнести лаконичность изложения доказательства, поэтому этот метод доказательства теорем и преобладает в учебниках при изложении доказательств.

Рассмотрим пример доказательства синтетическим методом и снабдим их комментариями.

ПРИМЕР 1. Известно, что 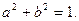Докажите, что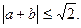

Доказательство. Рассмотрим очевидное неравенство 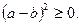(Почему именно это неравенство, а не другое?)

Перепишем это неравенство следующим образом: 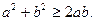(Почему именно так, а не иначе?)

Добавим к обеим частям последнего неравенства 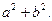Получим 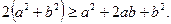(Зачем?)

Заменим в левой части (Почему не в правой?) 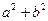на 1, получим, 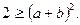Извлекая квадратный корень из обеих частей, получим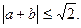

Неравенство доказано.

Дата добавления: 2014-08-04; просмотров: 343; Нарушение авторских прав

Мы поможем в написании ваших работ!