Их произведение равно 1, а, следовательно, по предположению индукции

х₁+х₂+…+х_k-1+x_kx_k+1³k.

Прибавим к обеим частям последнего неравенства x_k + x_k+1, перенесем x_kx_k+1 направо и преобразуем правую часть неравенства:

х₁+х₂+…+х_k+x_k+1³k - x_kx_k+1+ x_k + x_k+1=k+1+x_k(1- x_k+1)+ x_k+1-1= k+1+(1- x_k+1) (x_k-1)³k+1.

Таким образом, из истинности утверждения при n=k вытекает его истинность при n=k+1.

ПРИМЕР 3. Докажите, что число А_n=10ⁿ+18n-28 кратно 27 для всех натуральных n.

Доказательство. 1. При n =1, А₁=0, очевидно, кратно 27.

1. Пусть А_n кратно 27 при n = k, и докажем делимость А_n при n = k+1.

Имеем А_k+1=10^k+1 + 18(k+1) - 28 =10A_k - 162k + 270 = 10A_k + 27(10 - 6k), что доказывает делимость на 27. На основании метода математической индукции, заключаем, что А_n кратно 27 при любом натуральном n.

Рассмотрим некоторые обобщения принципа математической индукции.

Пусть р - некоторое целое число.

Предложение А(к), где к целое, истинно для всех целых значений к³р, если выполнены следующие два условия:

1) Предложение А(к) истинно для к=р.

2) Из предположения, что А(к) истинно для к=n (n - целое, n ³р), следует, что оно верно для следующего значения к=n + 1.

ПРИМЕР 4. Доказать, что любую сумму денег, большую 7 копеек, можно разменять трехкопеечными и пятикопеечными монетами.

Доказательство. Пусть сумма равна n копейкам. Если n = 8, то утверждение верно. Пусть утверждение верно для n=к. Могут представиться только два случая для размена суммы в к копеек.

а) потребовались только трехкопеечные монеты,

б) потребовалась хотя бы одна пятикопеечная монета.

В случае а) удаляем три трехкопеечные монеты и добавляем две пятикопеечные и тем самым размениваем сумму в к+1 копеек. В случае б) удаляем одну пятикопеечную монету и добавляем две трехкопеечные и тем самым размениваем сумму в к+1 копеек.

Приведем пример применения метода математической индукции в геометрии.

ПРИМЕР 5. Докажите, что количество диагоналей выпуклого к-угольника подсчитывается по формул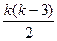е , где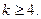

Доказательство. Очевидно, формула верна при n=4. Предположим, что она верна и в случае n-угольника и докажем ее для (n+1)-угольника. Рассмотрим (n+1)-угольник A₁A₂…A_nA_n+1. Проведем отрезок A_nA₁. Он разобьет наш (n+1)-угольник на n-угольник A₁A₂…A_n и треугольник A_nA₁А_n+1. Тогда количество диагоналей n-угольника A₁A₂…A_n равно 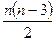и к ним еще прибавятся диагонали, которые получаются соединением вершины А_n+1 с вершинами A₂, A₃, … , A_n-1 и диагональ A_nA₁, т.е. добавится n-1 диагональ. Но тогда их общее количество будет равно 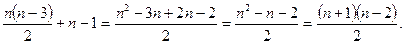На основании метода неполной математической индукции заключаем, что формула верна для любого выпуклого n-угольника.

Дата добавления: 2014-08-04; просмотров: 344; Нарушение авторских прав

Мы поможем в написании ваших работ!