Студопедия

Главная страница Случайная лекция


Мы поможем в написании ваших работ!

Порталы:

БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика



Мы поможем в написании ваших работ!




Уравнение совместности деформаций, выраженное через функцию напряжений

Читайте также:
  1. D. 17.1.22.11). - Maндатарий может отказаться от договора так, чтобы за мандан­том осталось ненарушенным право с удобством устроить то же дело лично или через другого мандатария.
  2. Адиабатический процесс. Уравнение Пуассона
  3. Алгоритм расчета теплопередачи через непроницаемые стенки
  4. Астрономическая, когда наблюдаемый объект находится на бесконечно большом расстоянии, ЭМВ проходят через всю толщу атмосферы и наблюдения выполняют с поверхности Земли.
  5. В каких случаях задача определения напряжений считается плоской?
  6. В случае одновременного наличия органов лицо выполняющее функцию единоличного органа оно же возглавляет и коллегиальный.
  7. Ввод и вывод данных через ячейки таблицы
  8. Власть эксперта (влияние через разумную веру).
  9. Волновое уравнение
  10. Волновое уравнение

Подставим выражения напряжений через функцию напряжений в уравнение совместности деформаций в напряжениях, которое при отсутствии объемных сил имеет вид

Так как сумма нормальных напряжений равна

,

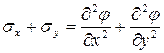то уравнение совместности деформаций принимает вид

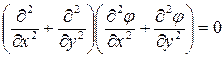
Это бигармоническое уравнение, которое встречается также в развернутом виде

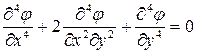
или, если ввести оператор Лапласа

,

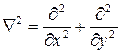уравнение может быть записано сокращенно

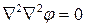или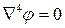

В последнем выражении оператор 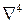называют бигармоническим оператором

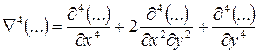
<== предыдущая страница | следующая страница ==>
Функция напряжений | Формулировка граничных условий для функции напряжений. Рамная аналогия профессора Папковича

Дата добавления: 2014-07-19; просмотров: 377; Нарушение авторских прав



Мы поможем в написании ваших работ!
lektsiopedia.org - Лекциопедия - 2013 год. | Страница сгенерирована за: 0.005 сек.