
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Волновое уравнение. Если взять rot от первых двух уравнений Максвелла, то получатся известные вам волновые уравнения, используемые в задачах нахождения распределения и
Если взять rot от первых двух уравнений Максвелла, то получатся известные вам волновые уравнения, используемые в задачах нахождения распределения и возбуждения волн. Получим их.
Из аналитической геометрии (или векторной алгебры) известно соотношение: rot(rot a) ≡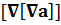 = ≡(
= ≡(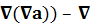 2a= grad(div a) –
2a= grad(div a) – 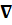 2a
2a
Тогда после взятия rot от первых двух уравнений Максвелла (6) получим:
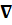 2H–
2H– 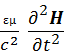 =
=  grad ρm + εоε
grad ρm + εоε 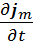 – rot je
– rot je
(7)
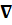 2E–
2E– 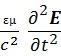 =
=  grad ρe + μоμ
grad ρe + μоμ 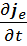 + rot jm
+ rot jm
Можно увидеть дуализм в уравнениях (7). При переходе от первого ко второму и наоборот надо производить замену E ↔ H,ε ↔ –μ, jе↔ –jm,ρе ↔ – ρm.
Уравнения (7) используют в задачах возбуждения полей некими зарядами и токами (антеннами).
|
|
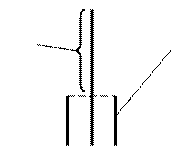 Pe = ρele – диполь Герца – линейная антенна
Pe = ρele – диполь Герца – линейная антенна
| |||
 | |||
|


|

 Pm = ISn– рамочная антенна, где S – площадь кругового тока, n– единичный вектор или нормаль к контуру, направление которого связано с направлением тока в контуре правилом правого винта (при вращение ручки буравчика по направлению движения часовой стрелки, совпадающем с направлением кругового тока остриё буравчика указывает направление вектора Pm).
Pm = ISn– рамочная антенна, где S – площадь кругового тока, n– единичный вектор или нормаль к контуру, направление которого связано с направлением тока в контуре правилом правого винта (при вращение ручки буравчика по направлению движения часовой стрелки, совпадающем с направлением кругового тока остриё буравчика указывает направление вектора Pm).
Если в уравнении (7) нет токов и зарядов (ρm, ρе, jе, jm = 0), то (7) принимает вид:
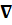 2H–
2H– 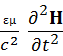 = 0
= 0
(8)
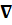 2E–
2E– 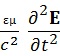 = 0
= 0
Напомним – это при ε и μ – константы.
1.2. В интегральной форме уравнения Максвелла имеют вид:
в СГСЕ
 1) –обобщенный закон Био-Савара
1) –обобщенный закон Био-Савара
L S
Здесь: L – замкнутый контур, Hτ – тангенциальная составляющая вектора H к элементу контура 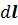 (это вектор, направление которого соответствует выбранному направлению обхода по контуру L);
(это вектор, направление которого соответствует выбранному направлению обхода по контуру L);
S – поверхность, натянутая на контур L и ограниченная им. Форма этой поверхности любая – плоская, выпуклая и т. д.
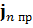 – нормальная составляющая плотности токов проводимости или стороннего к элементу поверхности
– нормальная составляющая плотности токов проводимости или стороннего к элементу поверхности 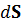 ;
;
Dn – проекция вектора D на нормаль к 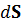 .
.
Первое слагаемое в подынтегральном выражении 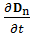 еще называют плотностью тока смещения.
еще называют плотностью тока смещения.
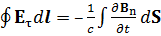 2)
2)
L S
– циркуляция вектора напряженности электрического поля E равна скорости изменения потока индукции магнитного поля B через поверхность S, натянутой на контур L, взятой с обратным знаком.
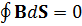 3) – это теорема Гаусса для вектора B
3) – это теорема Гаусса для вектора B
S
– она говорит об отсутствии магнитных зарядов (опытные данные).
В подынтегральном выраженииBn – проекция Bсоответствует его проекции Bn на нормаль к dS – элементу поверхности S.
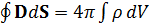 3) – это теорема Гаусса для вектора D
3) – это теорема Гаусса для вектора D
S V
Она является обобщенный закон взаимодействия зарядов. Здесь S – замкнутая поверхность, а V – внутренний объем, ограниченный этой поверхностью S. ρ – плотность сторонних зарядов.
Материальные уравнения те же
D = εE
B = μH
Описание электрического поля через электрический потенциал
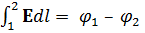
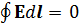 – циркуляция вектора E по замкнутому контуру L
– циркуляция вектора E по замкнутому контуру L
L
– физически это означает, что работа по перемещению единичного точечного заряда в статическом электрическом поле по замкнутой траектории равна нулю.
| <== предыдущая страница | | | следующая страница ==> |
| Уравнения Максвелла | | |
Дата добавления: 2014-02-28; просмотров: 543; Нарушение авторских прав

Мы поможем в написании ваших работ!