Волновое уравнение

Неразрывная связь параметров звукового поля характеризуется волновым уравнением, т.е. уравнением распространения звуковой волны в жидкости. При выводе волнового уравнения для простоты считают жидкость акустически однородной, представляющей собой сплошную среду (т.е. не имеющую никаких разрывов, в том числе и межмолекулярных промежутков) и изменения давления и плотности среды малыми.

Волновое уравнение выводится из трех частных уравнений, которые характеризуют те или иные физические явления в звуковом поле.

1. Уравнение неразрывности жидкости – это особая форма математического выражения закона сохранения массы через параметры звукового поля:

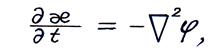
(2.7) где 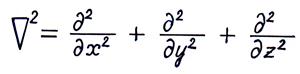- оператор Лапласа.

Уравнение (2.7) устанавливает зависимость между относительным изменением плотности среды æ и колебательной скоростью v (в проекциях).

2. Уравнение колебательного движения частиц жидкости – это второй закон Ньютона, представленный через параметры звукового поля (Напомню: второй закон Ньютона гласит: ускорение материальной точки пропорционально действующей на нее силе, обратно пропорционально массе точки и совпадает по направлению с силой):

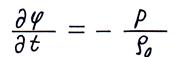или 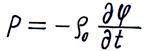. (2.8)

Уравнение (2.8) справедливо для волны любой формы, поскольку не зависит от координат.

3. Уравнение состояния жидкости. Это уравнение отражает зависимость только между давлением и плотностью, поскольку процесс сжатия жидкости можно считать адиабатическим т.е. без теплопередачи.

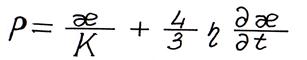, (2.9)

где К – адиабатический коэффициент сжимаемости жидкости ;

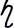- коэффициент динамической вязкости.

Уравнение (2.9) справедливо для волны любой формы.

В результате решения системы из (2.7), (2.8) и (2.9) относительно потенциала скорости 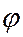получаем волновое уравнение распространения звука:

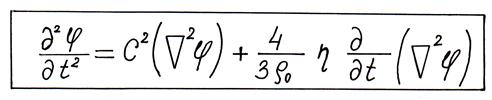(2.10)

где скорость распространения акустической волны

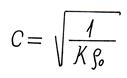. (2.11)

Волновое уравнение (2.10) позволяет определять основные параметры звукового поля для волны любого вида.

Хотя гидроакустические приборы излучают сферические волны, однако, с достаточной для практики точностью их можно считать плоскими. Если плоская волна распространяется в однородной вязкой безграничной жидкости вдоль оси , то = и волновое уравнение (2.10) принимает вид

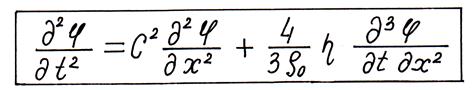(2.12)

Интеграл этого уравнения для бегущей волны в тригонометрической форме имеет вид

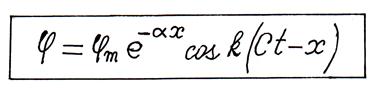, (2.13)

где — амплитуда потенциала скорости;

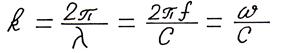— отношение угловой частоты к скорости звука, называемое волновым числом;

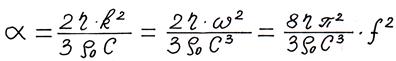— коэффициент затухания.

Воспользовавшись полученным значением потенциала скорости 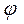можно определить основные параметры звукового поля:

· акустическое давление (ф. (2.8), (2.13)),

, (2.14)

где .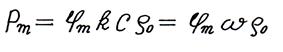

· линейную скорость колебаний (из ф.(2.6), считая, что в ультразвуковом поле ).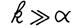

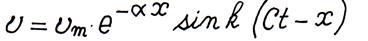, (2.15)

где ,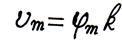

Из выражений (2.13) и (2.14) видно, что звуковое давление и колебательная скорость 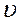изменяются синфазно. Таким образом, в зонах сгущения частиц, где 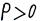, скорость 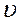положительна, вектор 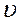совпадает с направлением распространения фронта волны, в зонах разряжения направлен в противоположную сторону.

Еще один параметр звукового поля удельное акустическое сопротивление. Оно определяется отношением звукового давления 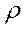к колебательной скорости

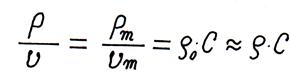. (2.16)

Удельное акустическое сопротивление воды примерно в 3500 раз больше , чем воздуха.

Распространение звуковых волн сопровождается переносом энергии. Энергетическая характеристика звукового поля – интенсивность звука I – это количество энергии, проходящей через единичную площадь за единицу времени. Для плоской волны

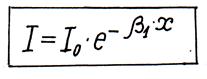, (2.17)

где I₀ – интенсивность звука в непосредственной близости от излучателя

;

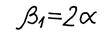— первый коэффициент поглощения звука, обусловленный ньютоновой вязкостью.

Рассмотренные выражения (2.14), (2.15), (2.17) показывают, что в однородной вязкой жидкости плоская звуковая волна затухает по экспоненциальному закону. Коэффициент затухания 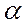прямопропорционален квадрату частоты f , что нужно учитывать при выборе частоты гидроакустических приборов.

Самостоятельно проработать вопросы: Скорость звука в море. Интерференция и дифракция звуковых волн. Рефракция. Реверберация. Отражательная способность грунта.

Дата добавления: 2014-08-04; просмотров: 690; Нарушение авторских прав

Мы поможем в написании ваших работ!