Уравнения Максвелла

Введение

Электродинамика – это очень большой раздел науки. Она является _eтеоретическим инструментом радиоинженера. Естественно, мы затронем только основополагающие вопросы электродинамики сплошных сред.

Данный курс посвящен: а) теории электромагнитных полей в материальных средах и в) теории макроскопических электрических и магнитных свойств веществ.

Мы рассмотрим некоторые вопросы распространения электромагнитных волн в материальных средах и, в частности, в некоторых радиотехнических устройствах, используемых в СВЧ (сверхвысокие частоты) (диапазон длин волн λ – 1 м – 0,1 мм) и оптическом диапазоне (λ – 0,1 мм – 0,1 μк) длин волн.

Из первой части курса «Теория поля», прочитанного вам в предыдущем семестре, вы узнали основные законы электродинамики, описывающие изменения и связь электрических и магнитных полей, которые описываются уравнениями Максвелла. В системе единиц СИ и СГСЕ они имеют вид:

СИ СГСЕ

rotH=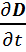 + j_erotH= 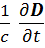+ 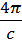j_e

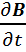rotE= –rotE= 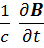(1)

divB =0 divB =0

divD =ρ_e divD =4πρ_e

где H, E, B и D есть векторы напряженности и индукции магнитного и электрического полей; ρ_е и j_е – объемные плотности электрического заряда и тока (вектор). При этом j_е=j_пр + j_стор +j_к есть сумма плотностей токов проводимости, стороннего и конвекционного.

Эти уравнения дополняются материальными уравнениями, связывающие между собой индукции напряженности полей:

СИ СГСЕ

B = μ_оμH B = μH(2)

D = ε_оεE D = εE,

где: ε_о ≈ 9*10^–12, [Ф/м] и μ_о ≈ 1,26*10^–6, [Гн/м] – электрическая и магнитная постоянные; а ε и μ – диэлектрическая и магнитная проницаемости среды, для вакуума ε = 1 и μ = 1. Константы ε_о и μ_о имеют следующую связь со скоростью распространения электромагнитных волн в вакууме c = 3*10⁸ [м/с]:

1/ε_оμ_о = c² (3)

Из уравнений (1) и (2) можно получить следующие уравнения:

j_пр = σE – закон Ома в дифференциальной форме

divj_е +– закон сохранения заряда (непрерывности).

Векторное электрическое поле Е можно описать через скалярный потенциал φ. Их связь имеет вид:

E = grad φ

Напомним (из векторной алгебры, или аналитической геометрии), что такое rot a, div a, grad a , где а(r) и а(r) некая векторная а и скалярная а функция координаты r. Они являются результатом соответствующего действия векторного оператора 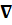(в прямоугольной системе координат он имеет вид 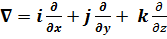,здесь i, j и k – единичные вектора в направлениях осей x, y и z , соответственно) на вектор а или скаляр а – rot a ≡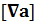(векторное произведение векторов), div a ≡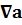и grad a ≡ 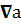(скалярные произведения векторов и вектора на скаляр, соответственно). В прямоугольной системе координат результат этих действии имеет вид:

rot a ≡= ) +) +),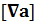

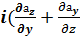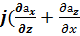div a ≡=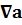

grad a ≡ =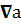

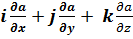
В уравнениях (1) и (2) ε и μ для различных сред могут быть функциями f(t, r, ω и т.д.) – от времени t, координаты r, частоты переменного электромагнитного поля ω и т. д.

Если ε и μ постоянные и не являются функциями переменных f(t, r, ω и т. д.) – например, для вакуума, то уравнения Максвелла упрощаются и принимают вид:

СИ СГСЕ

rotH= ε_оε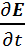 + j_erotH= 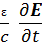+ 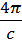j_e

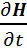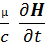rotE= –μ_оμrotE= (5)

divH =0 divH =0

divE =ρ_e/ ε_оε divE =4πρ_e/ ε

Уравнения (5) асимметричны относительно B и D. Для симметрии чисто формально вводят магнитные заряды ρ_m и токи j_m и тогда уравнения Максвелла (при ε и μ – константы) выглядят так:

rotH= ε_оε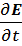 + j_erotH= 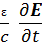+ 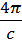j_e

rotE= –μ_оμ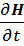– j_mrotE= 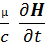– 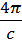j_m(6)

divH =ρ_m/ μ_оμ divH =ρ_m/ μ

divE =ρ_e/ ε_оε divE =4πρ_e/ ε

Дата добавления: 2014-02-28; просмотров: 338; Нарушение авторских прав

Мы поможем в написании ваших работ!