Изучение плоского движения твердого тела на примере маятника Максвелла

Цель работы: определение момента инерции маятника Максвелла и проверка формулы его поступательного движения.

Приборы и принадлежности: установка, разновес, секундомер, штангенциркуль, линейка.

Маятник Максвелла представляет собой однородный массивный металлический диск радиусом R. Через середину проходит стержень радиуса r, к концам которого прикреплены две нити (рис.1, вид сбоку). Стержень жестко связан с диском.

Маятник может участвовать в двух движениях: поступательном в вертикальной плоскости и вращательном вокруг своей геометрической оси. Это сложное движение обусловлено действием силы тяжести mg маятника. В состоянии покоя маятника его вес уравновешивается силой натяжения нитей. При движении маятника вниз сила натяжения нитей становится меньше, и поэтому весы, которые были уравновешены при покоящемся маятнике, выйдут из положения равновесия. Опустившись в крайнее нижнее положение, при котором нити полностью размотаны, маятник будет по инерции вращаться в том же направлении, вследствие чего нити начнут наматываться на стержень с другой стороны, маятник будет подниматься, меняя направление вращения.

Поступательное и вращательное движение маятника вниз – равноускоренное, вверх – равнозамедленное, ускорение центра масс в обоих случаях одинаково и равно:

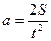, (1)

где S – путь, пройденный центром масс маятника в одном направлении; t – время движения маятника в одном направлении.

нить F_н

r O R

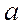
mg

Рис. 1. Маятник Максвелла.

Поступательное движение центра масс маятника массой m описывается уравнением:

ma = mg - F_H, (2)

где F_H – сила натяжения нитей. А вращение маятника уравнением:

Jε = M, (3)

где ε – угловое ускорение маятника; М – момент сил натяжения нитей; J – момент инерции маятника. Угловое ускорение ε можно определить из соотношения:

а = εr, (4)

где r – радиус стержня.

Момент сил натяжения нитей определяется следующим образом:

M = F_H r. (5)

Из уравнений (1), (3), (4), (5) можно выразить момент инерции маятника Максвелла:

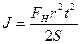. (6)

Дата добавления: 2014-11-08; просмотров: 422; Нарушение авторских прав

Мы поможем в написании ваших работ!