
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Уравнения шкал приборов различных систем
| Тип измерительной системы прибора | Уравнение шкалы |
| Магнитоэлектрическая | L = SI.I0; L = SU.U0 |
| Электромагнитная | L = SI.I2; L = SU.U2 |
| Электродинамическая и ферродинамическая | L = SI.I1.I2.Соs(φ) |
В зависимости от измерительной системы прибора (часто говорят просто, системы прибора) их шкалы могут быть либо линейными, либо нелинейными (равномерными и неравномерными).
Шкала прибора при любом пределе измерения имеет N делений.
Для измерения величины, вызывающей отклонение стрелки измерительного прибора, необходимо определить предел измерения Апр – количество единиц измеряемой величины, при которых стрелка отклоняется на всю шкалу (находится в крайнем правом положении), и цену деления шкалы – количество единиц измеряемой величины, при которых стрелка отклоняется на одно деление:
С= 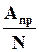 . (1.1)
. (1.1)
Тогда измеренное значение величины определится:
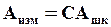 , (1.2)
, (1.2)
где Ашк – количество делений, на которые отклонилась стрелка прибора при измерении.
При каждом выборе предела измерения меняется цена деления прибора.
При измерении мощности с помощью ваттметра его цена деления определяется двумя параметрами: выбранными пределами катушки напряжений Uпр и тока Iпр:
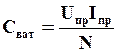 . (1.3)
. (1.3)
Паспортные данные измерительных приборов обычно приводятся на их шкалах. Расшифровка этих символов приведена в табл. 1.2.
Таблица 1.2
Условные обозначения на шкалах измерительных приборов
| Наименование системы приборов | Условное обозначение |
| Магнитоэлектрический прибор | 
|
| Электромагнитный прибор | 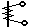
|
| Электродинамический прибор | 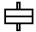
|
| Индукционный прибор | 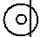 
|
| Ферродинамический прибор | 
|
| Электростатический прибор | 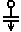
|
| Амперметр | А |
| Вольтметр | В |
| Ваттметр | W |
| Измеритель cos φ | φ |
Электрические измерения разделяют на прямые и косвенные. При прямых измерениях измеряемая величина отсчитывается непосредственно по шкале прибора. Примером прямых измерений служит измерение напряжения или тока соответственно вольтметром или амперметром. При косвенных измерениях искомую величину определяют расчетом на основании нескольких величин, полученных прямыми измерениями. Примерами косвенных измерений служит измерение сопротивления или мощности в цепи с помощью амперметра и вольтметра.
Точность измерения характеризуется возможными погрешностями, которые подразделяются на относительные (δА) и абсолютные (ΔА), а также на основные и дополнительные.
Абсолютная погрешность определяется как разность меду истинным Аист и измеренным Аи значениями физической величины А:
ΔА=±(Аист–Аи) . (1.4)
Так как истинное значение величины никогда не известно, то можно использовать оценку измеряемой величины как среднее арифметическое из многих измерений. Чем больше измерений, тем ближе оценка измерения совпадает с истинным значением величины:
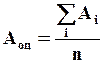 , (1.5)
, (1.5)
Ai – значение i-го измерения,
n – количество измерений.
Относительная погрешность измерения определяется отношением абсолютной погрешности к истинному значению измеряемой величины. Так как истинное значение не может быть известно, то достаточно точно относительную погрешность можно определить соотношением абсолютной погрешности и измеренного значения величины:
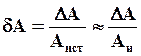 100 %. (1.6)
100 %. (1.6)
Относительную погрешность обычно выражают в процентах измеряемой величины.
На практике абсолютную погрешность ΔА определяют на основании гарантируемой заводом-изготовителем измерительного прибора точности измерения, которую обозначают классом точности прибора.
Класс точности указывается на шкале прибора числом. Класс точности равен относительной погрешности измерения прибора при измерении максимального для данного предела значения измеряемой величины Апр, выраженной в процентах:
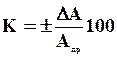 % (1 .7)
% (1 .7)
Тогда абсолютную погрешность измерения можно определить:
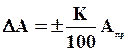 . (1.8)
. (1.8)
При использовании многопредельных приборов предел измерения необходимо выбирать, постепенно переходя от максимального значения к тому пределу, при котором измерение будет сделано с требуемой точностью. Это произойдет тогда, когда стрелка прибора отклонится на наибольший угол (обычно это правая половина шкалы прибора). Это позволяет при измерении избежать поступления на измерительную систему большего, чем допустимо, напряжения, что может вызвать выход из строя измерительной системы.
При определении погрешности при косвенных измерениях следует учитывать, что каждая из используемых при получении результата величин измерена с погрешностью, поэтому и общая погрешность будет увеличиваться:
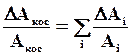 , (1.9)
, (1.9)
где Aкос и ΔAкос – измеренное значение и абсолютная погрешность измерения величины при косвенных измерениях;
Ai и ΔAi – измеренное значение и абсолютная погрешность измерения i-й величины при прямых измерениях.
Откуда абсолютная погрешность при косвенных измерениях:
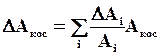 . (1.10)
. (1.10)
Например, абсолютная погрешность косвенного измерения мощности зависит от погрешности прямых измерений тока и напряжения:
 . (1.11)
. (1.11)
При этом абсолютные погрешности измерения напряжения и тока определяются по формуле (1.8).
Из выражения (1.8) следует, что в любой точке шкалы и при любом пределе Апр значение относительной погрешности δА будет одним и тем же.
Так как все измерения происходят с погрешностями, то при построении графиков по экспериментальным данным следует проводить сглаживающую линию, которая будет проходить не по самим точкам, а вблизи их, так чтобы быть в среднем максимально близко ко всем точкам, полученным в эксперименте (рис.1.1).
Экспериментальные точки с координатами Х и У при выбранных масштабах по осям 0Х и 0У наносятся на лист бумаги. Далее они мысленно соединяются прямыми линиями, и после этого проводится искомая зависимость таким образом, чтобы выполнялось условие
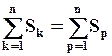 , (1.12)
, (1.12)
где Sk и Sp – площади между проведённой кривой и ломаной линией выше и ниже искомой.
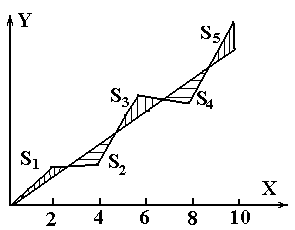 |
Рис. 1.1. Построение графика по экспериментальным точкам
Порядок выполнения работы и обработки результатов
1. По заданию преподавателя запишите в виде таблицы характеристики измерительных приборов стенда: назначение прибора; система; заводской номер; класс точности; пределы измерений; внутреннее сопротивление; диапазоны рабочих частот; шкала прибора; цена деления.
2. Включите стенд и проведите измерения напряжений источников питания стенда U1, U2 , U3. Вычислите погрешности измерений. Результаты измерении занесите в табл. 1.3.
Таблица 1.3
Дата добавления: 2014-10-14; просмотров: 599; Нарушение авторских прав

Мы поможем в написании ваших работ!