ОБЩЕТЕОРЕТИЧЕСКИЕ ОСНОВЫ КУРСА

1.1. Агрегатные состояния

Состояние данной массы газа определяется тремя величинами (параметрами): давлением p, объемом V и температурой T. Эти величины связаны между собой функциональной зависимостью, которая может быть представлена соотношением f (p, V, T) = 0, называемым уравнением состояния. Уравнение состояния идеального газа выводится из трех законов – Бойля – Мариотта, Гей-Люссака и Авогадро. Реальные газы подчиняются этим законам тем точнее, чем меньше давление и выше температура [1].

Закон Бойля – Мариотта. При постоянной температуре объем данной массы обратно пропорционален давлению. Если V₁ и V₂ – объемы газа при давлении p₁ и p₂ соответственно, то

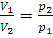
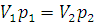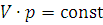, или (1.1)

Из закона Бойля – Мариотта вытекает следствие: при постоянной температуре плотность газа ρ пропорционально его давлению:

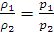(1.1a)

Законы Гей-Люссака и Шарля. При постоянном давлении с повышением температуры на 1°С объем данной массы газа увеличивается на 1/273,15 его объема при 0°С:

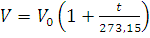(1.2)

где V – объем газа при температуре t °С, а V₀ – объем газа при 0°С.

При замене шкалы Цельсия абсолютной температурной шкалой (шкалой Кельвина), для которой T=273,15+t, этот закон можно сформулировать следующим образом: при постоянном давлении объем данной массы газа пропорционален его абсолютной температуре:

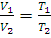(1.3)

где V₁ и V₂ – объемы газа при абсолютных температурах T₁ и T₂

При постоянном объеме зависимость давления данной массы газа от температуры записывается уравнениями, аналогичными (1.2) и (1.3):

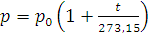(1.4)

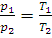(1.5)

Объединенный закон Бойля – Мариотта – Гей-Люссака выражается уравнением:

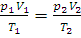(1.6)

где p₁ – давление и V₁ – объем данной массы газа при абсолютной температуре T₁, p₂- давление и V₂ – объем той же массы газа при абсолютной температуре T₂.

Закон Авогадро: в равных объемах различных газов при одинаковых условиях содержится равное число молекул.

Число молекул (N_A) в 1 моль вещества одинаково у всех веществ и равно 6,02·10²³ (число Авогадро). Следовательно, количества веществ 1 моль, находящихся в газообразном состоянии при одинаковой температуре и одинаковом давлении, занимают равные объемы. При нормальных условиях (температура 0°С и давление = 1,01325·10⁵ Па) объем 1 моль газа равен 22,414л.

Уравнение состояния идеального газа – уравнение Менделеева – Клайперона для одного моля газа имеет вид:

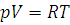(1.7)

а для любого количества газообразного вещества:

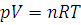(1.8)

где R – универсальная газовая постоянная, числовое значение которой зависит от единиц измерения других величин. Величина ее выражается в единицах СИ Дж/(моль·К).

Уравнение (1.8) может быть использовано для определения относительной молекулярной массы М_ч. Заменяя в нем величину n отношением m/M, где m – масса газа, а M – молярная масса данного газа, и решая его относительно M, получим:

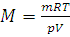(1.9)

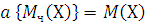
Закон Дальтона: общее давление смеси газов равно сумме парциальных давлений составных частей (компонентов):

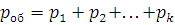(1.10)

где p_об – общее давление смеси газов, p₁, p₂, p_k – парциальные давления компонентов смеси. Парциальным давлением называется давление каждого компонента, если бы он один занимал объем, равный объему смеси той же температуре.

Уравнения (1.8) и (1.9) применимы к смесям газов, химически не взаимодействующих друг с другом, а также к каждому компоненту смеси. В первом случае n – общее количество вещества компонентов (n=n₁+n₂+…+n_k=∑n_i, где i=1, 2, …, k), M – средняя «смешанная» молярная масса, во втором случае n – количество вещества каждого компонента, т.е. n₁, n₂, …, n_k, p – парциальное давление компонента, V – общий объем смеси.

Зависимость между парциальными давлениями и общим выражается уравнениями:

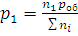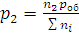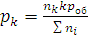, , …, (1.11а)

Отношения n₁/∑n_i, n₂/∑n_i, …, n_k/∑n_i, называют молярными долями данного компонента. Если молярную долю обозначить через x, то парциальное давление любого i-го компонента смеси (где i = 1, 2, …, k) будет равно:

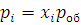(1.11б)

Таким образом, парциальное давление каждого компонента равно произведению его молярной доли на общее давление смеси.

Для идеальных газов молярная доля x равна объемной доле φ (V₁/∑υ_i, V₂/∑υ_i, …, V_k/∑υ_i). Если состав смеси выражен в объемных долях (%), то φ^'

φ₁'/100 = x₁, φ₂'/100 = x₂, …, φ_k'/100 = x_k, (1.12)

Кинетическая теория газов. Основным уравнением кинетической теории газов для 1 моль является уравнение:

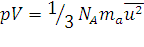, (1.13)

где m_a – масса молекулы; ū – средняя квадратичная скорость молекул; N_A – число молекул в 1 моль. Для любого количества вещества в уравнении вместо N_A входит N.

Из основного уравнения кинетической теории газов можно вывести изложенные выше газовые законы и некоторые новые положения.

Сопоставляя уравнения (1.7) и (1.13) получим для 1 моль газа:

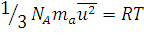, (1.14)

1. Отсюда находим среднюю квадратичную скорость молекул:

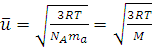(1.15)

где M = N_A·m_a – молярная масса газа.

Из этого уравнения следует, что для одного и того же газа средняя квадратичная скорость молекул прямо пропорциональна корню квадратному из абсолютной температуры:

(1.16)

где ū₁ – средняя квадратичная скорость при температуре T₁, а ū₂ –то же самое при T₂.

Для различных газов при одинаковой температуре средняя квадратичная скорость молекул обратно пропорциональна корню квадратному из относительных молекулярных масс:

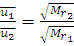(1.17)

Здесь ū₁ и 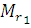относятся к первому газу, а ū₂ и 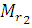- ко второму.

2. Из уравнения (1.14) находим:

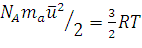(1.18)

Выражение, стоящее в левой части этого равенства, есть средняя кинетическая энергия поступательного движения молекул идеального газа в количестве вещества 1 моль. Обозначив ее через Е, получим:

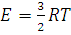(1.19)

Разделив обе части уравнения (1.18) на N_A, найдем, что средняя кинетическая энергия поступательного движения одной молекулы газа равна:

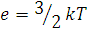(1.20)

где 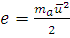, а 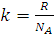- константа, называемая постоянной Больцмана.

Следовательно, кинетическая энергия идеального газа пропорциональна абсолютной температуре.

Примеры

1. В баллоне емкостью 20 л находится водород под давлением 162·10⁵ Па. Сколько шаров-пилотов можно наполнить водородом, если объем шара равен 200 л и давление в нем должно быть равно 2·10⁵ Па? Водород при этих условиях считать идеальным газом.

Решение. Так как температура и масса газа остаются постоянными, то для решения задачи применим закон Бойля – Мариотта (1.1). После наполнения шаров-пилотов объем водорода (V₂) буде равен:

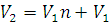
где V₃ – объем одного шара; n – число шаров; V₁ – объем баллона, в котором водород после наполнения последнего шара находится под давлением 2·10⁵ Па. Заменив в уравнении (1.1) V₂ его значением, получим:

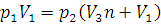
Отсюда

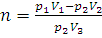
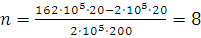
Находим, что водородом можно наполнить восемь шаров-пилотов.

2. При нормальных условиях плотность азота равна 1,25 г/л. Определить плотность газа при 0°С и давлении 5,065·10⁵ Па.

Решение. Требуется определить плотность азота при 0°С и давлении 5,065·10⁵ Па. Из уравнения (I, 1а) находим ρ₂ – плотность при давлении p₂:

;

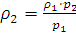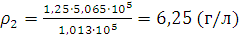
3. При постоянном давлении открытая двухлитровая колба охлаждается от 200 до 0°С. Насколько увеличится масса воздуха в колбе, если плотность воздуха при нормальных условиях равна 1,293 г/л? Изменением объема колбы вследствие охлаждения стекла пренебречь.

Решение. Объем одного и того же количества газа согласно закону Гей-Люссака при 0°С должен быть меньше, чем при 200°С. Если при t₂ = 0°С его объем V₂ = 2 л, то при t₁ = 200°Сон может быть определен из уравнения (1.3):

;

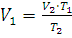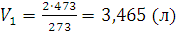
При 0°С масса газа в двухлитровой колбе равна 1,293x2=2,586 (г). При 200°С такую же массу будет иметь 3,465 л. Таким образом, если температура понизится с 200°С до 0°С, то в колбу войдет 3,465-2=1,465 (л) воздуха; соответствующая масса может быть определена из пропорции:

;

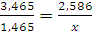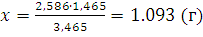
Следовательно, масса газа в колбе увеличится на 1,093 г.

4. Смесь эквивалентных количеств этана и кислорода находится в замкнутом сосуде при температуре 15°С и давлении 1·10⁵ Па. Каково будет давление после взрыва смеси и приведения содержимого сосуда к первоначальной температуре?

Решение. Напишем уравнение реакции горения этана:

2С₂Н₆ + 7О₂ = 4СО₂ + 6Н₂О

Вода при температуре 15°С будет в жидком состоянии, и при подсчета числа молекул не нужно учитывать образовавшихся молекул воды (так как объем жидкости по сравнению с объемом газа той же массы несоизмеримо мал). Из уравнения следует, что из 9 молекул исходных веществ образовалось 4 молекулы. Так как объем газов и температура остаются постоянными, то с уменьшением числа молекул в 9/4 раза и давление должно уменьшиться в такое же число раз, т.е. оно будет равно: 1·10⁵:9/4=0,4·10⁵ Па.

5. Для хлорирования питьевой воды хлор доставляется в баллонах под давлением. Давление в этих баллонах равно ,722·10⁵ Па при 0°С и 15,47·10⁵ Па при 30°С. Можно ли считать хлор в этих условиях идеальным газом?

Решение. Так как в баллоне объем постоянен, то для идеального газа, как следует из уравнения (I, 5), - величина постоянная. Вычисляем это отношение для хлора: при 0°С 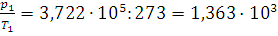, а при 30°С 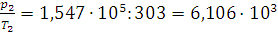. Оно непостоянно. Следовательно, хлор в этих условиях считать идеальным газом нельзя.

6. При температуре 18°С и давлении 98,64 кПа объем газа равен 2 л. Привести объем газа к равным нормальным условиям.

Решение. Из уравнения (1.6) находим V₁ – объем при нормальном давлении 1,013·10⁵ Па и температуре 273 К. Данные задачи переводим в единицы СИ:

;

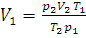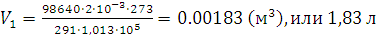
7. Вычислить при нормальных условиях газовую постоянную R, выразив ее в: а) Па·м³/(моль·К); б) Дж/(моль·К).

Решение. Из уравнения (1.7) находим: 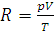. Подставляем в эту формулу числовые значения: p=1.01325·10⁵Па, Т-273,15 К и V_m=2,2414·10^-2 м³ (молярный объем газа):

а) ;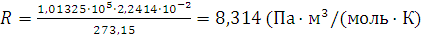

б) 8,314 Па·м³/(моль·К) = 8,314 Н/м² · м³/(моль·К) = 8,314 Дж/(моль·К).

8. Какое количество вещества и какая масса кислорода находится в газометре емкостью 10 л при 20°С и под давлением 100 кПа?

Решение. Решаем уравнение (1.8) относительно n: 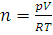. Данные задач подставляем в уравнение в единицах СИ: R=8,314 Дж/(моль·К), p=1·10⁵ Па, Т=273+20=293 К, V=0,01 м³:

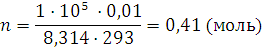
m = nM ; m = 0,41 · 32 = 13,12 (г)

9. По методу В. Майера определялась относительная молекулярная масса этилового эфира. При испарении эфира массой 0,0856 г его пары вытеснили в эвдиометрическую трубку воздух объемом 29,2 мл; высота водяного столба в эвдиометрической трубке 22,5 см, температура воздуха 17°С, атмосферное давление 1005 гПа. Давление насыщенного пара воды при 17°С равно 19,37гПа. Вычислить относительную молекулярную массу эфира и найти относительную ошибку опыта в процентах.

Решение. Давление сухого воздуха, заключенного в эвдиометрической трубке, будет равно:

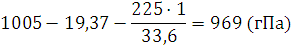
где 1 – значение плотности воды и 13,6 – значение плотности ртути. Подставляем в уравнение (I, 9) соответствующие значения, выразив их в единицах СИ, получаем:

;

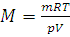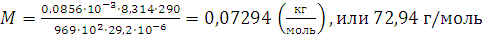
Таким образом, относительная молекулярная масса эфира равна 72,94. Относительная ошибка в процентах равна:

(74,08-72,94)·100:74,08-1,54 %

где 74,08 – табличная величина относительной молекулярной массы эфира.

10. Смешаны водород объемом 3 л и под давлением 2·10⁵ Па с кислородом объемом 2 л под давлением 1·10⁵ Па. Общий объем смеси равен 4 л. Определить парциальные давления газов и общее давление смеси.

Решение. Водород, занимавший объем V₁, равный 3 л, при давлении p₁ равном 2·10⁵ Па, после смешивания с кислородом распространится в объеме V₂, равном 4 л. Парциальное давление водорода , равное p₂, находим из закона Бойля – Мариотта (1.1):

; .

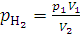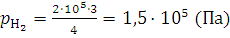Парциальное давление кислорода находим аналогичным способом:

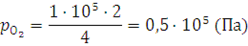
Общее давление p смеси равно: 1,5·10⁵ + 0,5·10⁵ = 2·10⁵ (Па).

11. Смесь из 2 моль азота, 3 моль кислорода и некоторого количества вещества аммиака при 20°С и давлении 4·10⁵ Па занимает объем 40 дм³. Вычислить количество аммиака в смеси и парциальное давление каждого из газов.

Решение. Из уравнения (1.8) находим n – общее количество всех газообразных веществ, составляющих смесь, и подставляем R, равное 8,314 Дж/(моль·К), p = 4·10⁵ Па, V = 4·10^-2 м³, T =273+20 = 293 К :

;

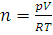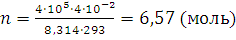
Количество вещества аммиака

n (NH₃) = 6,57 – 2 – 3 = 1,57 (моль)

Парциальное давление газов вычисляем по уравнению (1.11а):

p (N₂) = 4·10⁵ · 2 : 6,57 = 1,217·10⁵ (Па);

p (O₂) = 4·10⁵ · 3 : 6,57 =1,826·10⁵ (Па);

p (NH₃) = 4 · 10⁵ · 1,57 : 6,57 =0,956·10⁵ (Па).

12. 0,5 моль водорода и 0,25 моль азота находятся в газометре вместимостью 5 л при 10°С. Вычислить парциальное давление каждого из газов и состав смеси в объемных долях.

Решение. Парциальное давление каждого компонента находим из уравнения (1.8):

;

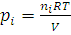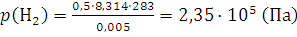
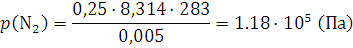
По формуле (1.12) вычисляем содержание водорода и азота в объемных долях:

;

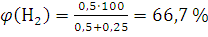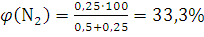
13. Какое давление будет иметь при 0°С кислород объемом 10 л и количеством вещества 0,25 моль? Средняя квадратичная скорость молекул кислорода при этой температуре равна 461 м/с.

Решение. Из формулы (1.13) находим давление, подставляя значения в единицах СИ: 10 л равны 0,01 м³, масса газа (N·m_a) равна произведению молярной массы на количество вещества, т.е. 0,032 кг/моль · 0,25 моль = 0,008 кг:

;

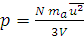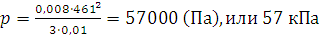
14. При какой температуре средняя квадратичная скорость молекул хлора будет равна 500 м/с?

Решение. Из формулы (1.14) находим T:

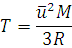
Подставляем значения, выражая их в СИ: ū в м/с, М в кг/моль, а R в Дж/(моль·К), и получаем:

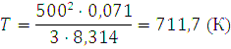
Следовательно, температура t будет равна:

711,7 – 273 = 483,7 (°С)

1.2. Химическая термодинамика

1.2.1. Первый закон термодинамики

Первый закон термодинамики есть закон сохранения энергии в применении его к термодинамическим процессам. Можно дать несколько, по существу равноценных, формулировок этого закона:

а) общая энергия изолированной системы остается постоянной независимо от каких бы то ни было изменений, происходящих в этой системе;

б) изменение внутренней энергии системы (∆U) равно разности между количеством сообщенной системе теплоты q и количеством работы А, совершенной системой.

Математическое выражение первого закона термодинамики будет иметь вид:

∆U = q - A (2.1)

q - считается положительной, если теплота поглощается систе­мой, и отрицательной, если теплота выделяется [2].

Из первого закона термодинамики вытекает ряд следствий, имеющих большое значение для физической химии и решения раз­личных технологических задач. Мы ограничимся применением пер­вого закона термодинамики только для идеальных газов и рассмот­рим важнейшие процессы: изохорический, изобарический, изотер­мический и адиабатический.

Изохорический процесс

Изохорический процесс протекает при постоянном объеме, поэтому система никакой работы не совершает. В этом случае вся теплота расходуется на увеличение внутренней энергии системы. Если V - соnst, то A=0, тогда

q_V = ∆U

При изохорическом процессе количество теплоты, получае­мое системой, можно вычислить по уравнениям:

q_V = пС_V(Т₂ – T₁); (2.2)
q_V=nC_vT₁/T₂(p_2–p₁) (2.3)

гдеn — количество вещества; р₁ и р₂ — соответственно начальное и конечное давление системы; — молярная теплоемкость при постоянном объеме; T₁ — начальная температура; T₂ — конечная температура.

Изобарический процесс

Если теплота поглощается системойпри постоянном давлении, то в системе соответственно увеличивается энтальпия. Если р = const, то
∆U = qp - А, но ∆U + А = ∆H. Тогда q_p = ∆H (2.4)

Количество теплоты, получаемое системой в этих условиях, мо­жет быть вычислено по уравнениям:

q_р = nСр (Т₂ – T₁), (2.5)

q_p = 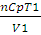(V₂ –V₁) (2.6)

где С_р — молярная теплоемкость при постоянном давлении; V₁ и V₂ -соответственно начальный и конечный объем системы.

Работа при изобарическом процессе выражается уравнением:

A=р(V₂ - V₁) (2.7)

Изотермический процесс

Если совершается изотермический процесс, то внутренняя энергия системы при этом не меняется. Вся сообщаемая теплота расходуется на работу по расширению системы.

Если T = сonst, то ∆U = 0, тогда q = A.

Работа изотермического расширения системы может быть вы­числена по уравнениям:

А = nRТ -2,3 lg 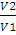; (2.8)

A = nRТ -2,3 lg 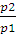(2.9)

Адиабатический процесс

При адиабатическом процессе теплообмен между данной систе­мой и окружающей средой отсутствует, поэтому q = 0. При этом система может совершать работу только за счет убыли внутренней энергии: А = -∆U. Работа в этом случае может быть вычислена по одному из следующих уравнений:

A= пС_v(T₁— T₂), (2.10)

A = 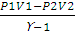, (2.11)

A = 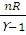(T_{1 –} T₂), (2.12)

ϒ = 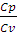(2.13)

Связь между давлением, объемом и температурой в начале и конце адиабатического процесса выражается уравнениями:

p₁V₁^ϒ = p₂V₂^ϒ; (2.14)

T₁V₁^ϒ-1 = T₂V₂^ϒ-1; (2.15)

Для одноатомных газов

C_v = R, а C_p = R (2.16)

Следовательно,

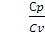= ϒ; ϒ = 1,67 (2.17)

Для двухатомных газов

C_v = R, a C_p = R (2.18)

Отсюда

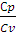= ϒ = 1,40 (2.19)

Примеры

1. Путем нагревания при постоянном давлении в 1,013∙10⁵ Па газу сообщено 2093,4 Дж теплоты. Определить изменение внутрен­ней энергии этого газа, если он при этом расширился от 0,01 до 0,02 м³.

Решение: Согласно первому закону термодинамики ∆U = q - А. Работа, совершенная газом при изобарическом расшире­нии, может быть вычислена по уравнению (2.7):

А = р (V₂ — V₁);

А = 1,013 . 10⁵ Па • (0,02 м³ - 0,01 м³) = 1013 Дж

Отсюда ∆U = 2093,4 - 1013 = 1080,4 (Дж).

2. Гелий массой 75 г нагревали при температуре 100 °С и давлении 1,013 • 10⁵ Па. Вычислить количество затраченной теплоты, если объем газа изменился от 3 до 15 л.

Решение: Так как нагревание газа происходит изотерми­чески и изобарически, то количество затраченной теплоты можно вычислить по уравнению (2.6), только дополнительно необходимо определить количество вещества п и молярную теплоемкость гелия при постоянном давлении:

n (Не) = 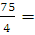18,75 (моль)

Гелий — одноатомный газ, поэтому согласно формуле (2.16)

Ср = • 8,314 = 20,79 (Дж/моль);

q_{p =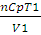} (V₂ – V₁)

q_p = 18,75•20,79•373/3• (15 – 3) = 581600 (Дж) или 582 кДж

3. Определить работу, совершаемую азотом при изотермическом (20 ºС) расширении его от 0,015 до 0,1 м³, если начальное давление было 3,039 • 10⁵ Па. Каково будет конечное давление?

Решение. Для изотермического процесса работа расшире­ния газа может быть вычислена по уравнению (2.8). Количество вещества азота находим из уравнения состояния идеального газа:

pV = nRТ;

n(N₂) = ;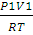

n(N₂) = 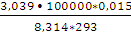= 1,875 (моль)

А = пКТ • 2,3lg ;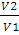

А= 1,875 • 8,314 • 293 • 2,3 lg 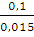= 8657 (Дж)

Конечное давление газа при постоянной температуре и извест­ном объеме находим по закону Бойля — Мариотта:

=

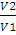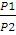
Отсюда

p₂ = ;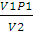

p₂ = 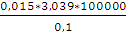= 45600 (Па)

4. Сколько нужно затратить теплоты, чтобы изохорически на­греть кислород массой 25 г от 0 до 50 °С?

Решение. При изохорическом процессе газ никакой работы не совершает, поэтому вся подводимая к газу теплота расходуется на его нагревание. Согласно уравнению (2.2)

q_v = nC_v(T₂ – T₁); п (0₂) = 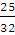= 0,781 (моль)

Для двухатомного газа

C_v = R

С = 2,5 • 8,314 = 20,79 (Дж);

q_v = 0,781 • 20,79 • (323 — 273) = 812 (Дж)

5. Навеску водорода массой 0,5 г, взятую при 25 °С, адиабатически сжимают от 6 до 2 л. Определить конечную температуру газа и работу, затраченную на его сжатие.

Решение. Связь между объемом и температурой адиабатиче­ского процесса показывает уравнение (2.14):

T₁V₁^ϒ-1 = T₂V₁^ϒ-1

Для двухатомного газа ϒ = 1,40. Из уравнения (2.14) находим Т₂:

Т₂ = 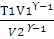; T₂ =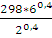

lgT₂ = lg 298 + 0,4lg 6 – 0,4lg2 = 2,6651;

T₂ = 462,5K

Для определения затраченной работы применим уравнение (2.10):

А = пС_v (T₁ — T₂); п (Н₂) = 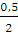= 0,25 (моль)

Для двухатомного газа С_v = 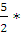8,314 = 20,79 (Дж);

А = 0,25 • 20,79 • (298 — 462,5) = -855 (Дж)

1.2.2. Термохимия

Тепловым эффектом реакции называют теплоту, выделенную или поглощенную в ходе химической реакции, протекающей необ­ратимо при постоянном давлении или постоянном объеме, причем температура исходных веществ (исх) и продуктов реакции (прод) одна и та же. В термодинамике положительной считают ту теплоту, которую подводят к системе (эта теплота поглощается системой), а отрицательной - ту, которую система выделяет. В термохимии приняты обратные обозначения.

Тепловой эффект химической реакции относят обычно к 1 моль образовавшегося вещества (обр). С этой целью нередко в термо­химических уравнениях коэффициенты следует брать дробными.

Из первого закона термодинамики (2.1) следует: q_v = ∆U; q_v = ∆H. Таким образом, тепловой эффект химической реакции при постоянном объеме представляет собой изменение внутренней энергии системы ∆U , а при постоянном давлении — изменение энтальпии ∆H . Разница между∆H и ∆U мала, если реакция идет между жидкими или твердыми веществами. В случае реакций с участием газообразных веществ это различие заметно. Если в реак­ции участвует п₁ моль, а получается п₂ моль газообразных веществ, то

∆H = ∆U +RT (n₂ — n₁) (2.20)

В термохимии чаще имеют дело с ∆Н.

Основным законом термохимии является закон Гесса (1840) — частный случай первого закона термодинамики: если процесс идет при постоянном давлении или при постоянном объеме, то тепловой эффект химической реакции зависит только от начального и конеч­ного состояния реагирующих веществ и не зависит от пути, по ко­торому реакция протекает. Из закона Гесса вытекают следствия:

1. Тепловой эффект химической реакции равен разности между суммой теплот образования получающихся веществ и суммой теплот образования вступающих в реакцию веществ (с учетом их стехио- метрических коэффициентов):

∆Н_реакц = ∑(∆Н_обр)_прод - ∑(∆Н _обр)_исх (2. 21)

2. Тепловой эффект химической реакции равен разности между суммой теплот сгорания (сгор) исходных веществ и суммой теплот сгорания продуктов реакции (с учетом их стехиометрических коэф­фициентов):

∆Н_реакц = ∑(∆H_сгор)_исх - ∑(∆H_сгор)_прод (2.22)

Величины стандартных теплот образования и теплот сгорания находят в справочниках. Значение закона Гесса состоит в том, что он позволяет определить тепловые эффекты таких реакций, которые или нереализуемы, или не могут быть проведе­ны чисто, т. е. без побочных процессов [2].

При растворении кристаллогидратов наблюдается более низ­кий тепловой эффект, чем при растворении безводной соли. Раз­ность между теплотой растворения безводной соли ∆H_безв и тепло­той растворения ее кристаллогидрата ∆H_кр есть теплота гидратации ∆H_гидр:

∆Н_гидр = ∆Н_безв - ∆Н_кр (2.23)

Примеры

1. Реакция горения ацетилена при стандартных условиях вы­ражается уравнением:

С₂Н₂ + 2 0₂ = 2С0₂+ Н₂О_ж, ∆Н = -1300 кДж

Определить теплоту образования ацетилена при постоянном давлении.

Решение. Для решения задачи данный химический процесс следует разбить на отдельные промежуточные стадии:

1) разложение ацетилена на углерод и водород:

С₂Н₂ = 2С + Н₂ + ∆ Н_х

2) образование углекислого газа из углерода и кислорода:

2С + 20₂ = 2С0₂ - 2 • 393,77 кДж

3) образование жидкой воды из водорода и кислорода:

Н₂ + 0₂ = Н₂О_ж - 285,96 кДж

Сумма тепловых эффектов всех стадий этого процесса и должна равняться общему тепловому эффекту горения ацетилена:

∆ Н_х - 787,54 - 285,96 = - 1300

∆Н_х = -226,5 кДж, ∆Н_х - теплота разложения ацетилена; сле­довательно, теплота образования ацетилена при стандартных усло­виях ∆Н^º₂₉₈ равна 226,5 кДж.

Теплоту образования ацетилена также можно определить, ис­пользуя следствие из закона Гесса (2.21), т. е. теплота горения аце­тилена будет равна сумме теплот образования 2 моль углекислого газа и 1 моль воды (жидкой) минус теплота образования 1 моль аце­тилена:

-2 • 393,77 - 285,96 - ∆Н^º₂₉₈ = -1300;

∆Н^º₂₉₈ = 226,5 кДж

2. Процесс алюминотермии выражается химическим уравнением:

8А1 + ЗFe₃0₄ = 4А1₂0₃ + 9Fe + ∆Н

Рассчитать, сколько выделится теплоты при сгорании 1 кг термита.

Решение. По теплотам образования участвующих в реакции веществ определим тепловой эффект реакции в целом. Для этого рассмотрим отдельно каждую стадию процесса:

1) ЗFе₃0₄ = 9Fе + 60₂ + 3 • 1117,82 кДж;

2) 8А1 + 60₂ - 4А1₂0₃ - 4 • 1670,5 кДж.

Алгебраическая сумма всех стадий процесса и будет составлять тепловой эффект реакции:

∆H = 3 • 1117,82 — 4 • 1670,5 = -3328,5 кДж

Из уравнения реакции следует, что 3328, 5 кДж теплоты выделяется при взаимодействии алюминия массой 216 г (8 • 27) и магнетита массой 696 г (3 • 232), т. е. при сгорании термита массой 912 г. При сгорании термита массой 1000 г выделится х кДж:

912 : 1000 = -3328,5 : х; х = -365 (кДж)

3. Вычислить тепловой эффект при постоянном давлении и постоянном объеме в стандартных условиях реакции:

С₂Н₅ОН_ж + 0₂ = СН₃СООН_ж + Н₂О_ж

Решение. Тепловой эффект реакции может быть рассчитан по теплотам образования участвующих в реакции веществ (2.21). Но в данном случае удобнее его рассчитать по тепловым эффек­там сгорания (2.22). В справочнике находим тепловые эффекты полного сгорания всех реагирующих веществ в кислороде. Теплота сгорания этилового спирта равна — 1367,7 кДж. Теплота сгорания СН₃СООН_ж равна — 872,1 кДж. Теплота сгорания Н₂О_ж равна нулю, так как она высший оксид, продукт полного сгорания водо­рода в кислороде:

∆Нреакц = - 1367,7 - (-872,1) = - 495,6 (кДж/моль)

∆U^º₂₈₉ рассчитываем по уравнению (2.20), но предварительно кило­джоули переведем в джоули:

∆U^º₂₈₉ = -495600 – 8,314 • 298 • (0 - 1); ∆U^º₂₈₉ = - 493 (кДж)

4. На сколько градусов повысится температура при растворении 0,5 моль серной кислоты в воде массой 400 г, если теплота растворе­ния серной кислоты равна — 74,94 кДж, а удельная теплоемкость раствора равна 3,77 Дж/(г • К)?

Решение. 74 940 Дж выделяются при растворении 1 моль кислоты. При растворении же 0,5 моль серной кислоты массой 49 г в воде массой 400 г образуется раствор массой 449 г и выделится 37 470 Дж (74 940 • 0,5). 3,77 Дж нагревают раствор массой 1 г на 1 °С, а 37 470 Дж нагревают на ∆t:

449 • 3,77 • ∆t = 37 470. Отсюда ∆t = 22,14 °С.

5. При растворении сульфата меди массой 8 г в воде массой
192 г температура повышается на 3,95 °С. Определить теплоту гидратации сульфата меди СuS0₄, если известно, что теплота раст­ворения СuS0_4,• 5Н₂0 равна 11 723 Дж. Удельная теплоемкость раствора равна 4,187 Дж/(г • К).

Решение. Для нагревания раствора массой 1 г на 1 °С по­требуется 4,187 Дж, а для нагревания раствора массой 200 г (8 + 192) на 3,95 °С потребуется:

4,187 • 200 • 3,95 = 3308 (Дж)

Следовательно, при растворении сульфата меди массой 8 г в воде массой 192 г выделяется 3308 Дж, а при растворении 1 моль (160 г) безводной соли выделится ∆H_безв.

Тогда 8:160 = -3308:∆H_безв;

∆H_безв= -66160 (Дж).
Из уравнения (2.23) находим теплоту гидратации:

∆Н_гидр = 66160 - 11723 = - 77 883 (Дж)

1.2.3. Второй закон термодинамики

Согласно второму закону термодинамики теплота самопроиз­вольно может переходить только от более нагретого тела к менее нагретому. Установлено, что в работу может превращаться только часть той теплоты, которая переходит от нагревателя к холодиль­нику, и тем большая, чем больше разность температур:

A = q 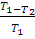(2. 24)

где q - теплота, отдаваемая нагревателем; T₁—температура на­гревателя; Т₂ — температура холодильника.

Отношение называется коэффициентом полезного действия (КПД) - η. Отсюда

η = 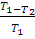(2.25)

На основе второго закона термодинамики Клаузиус ввел поня­тие энтропии S — термодинамической функции системы. Измене­ние энтропии ∆S в каком-либо процессе зависит только от начального и конечного состояний системы и не зависит от пути перехода.

Наиболее просто ∆S определяется для обратимых неизолирован­ных изотермических процессов:

∆S = (2.26)

где q — количество теплоты, сообщенное системе.

При изотермическом плавлении или испарении количества ве­щества 1 моль: ∆S = ∆H/T

где ∆H - теплота плавления или теплота испарения.

Если происходит изотермическое расширение п моль идеального газа, то

∆S =nR • 2,3lgV₂/V₁ (2.28)

∆S = nR2,31gp₁/p₂ (2.29)

Если же в системе, состоящей из идеального газа, изменяется одновременно несколько параметров, то

∆S = пС_v . 2,3lgT₂/T₁+ пR • 2,3 lgV₂/V₁ (2.30)

∆S = пС_p • 2,3lgT₂/T₁ + пR ∙2,3lg p₁/p₂ (2.31)

∆S = п • 2,3(C_vlg p₂/p₁ + C_plg(V₂/V₁) (2.32)

Вычисление ∆S в необратимых процессах ведут по уравнениям для процессов обратимых. Это вполне закономерно, так как изме­нение энтропии при заданном начальном и конечном состояниях системы не зависит от пути перехода и, в частности, от обратимости процесса. Если необратимый и обратимый процессы проводятся в одних и тех же граничных условиях, то
∆S_oбр =∆S _неoбр.[2].

Примеры

1. К котлу с водой, находящейся при 100 °С, подвели 8374 Дж теплоты. Найти КПД и максимальную работу, которую можно получить от котла, если температура холодильника 30 °С.

Решение. Максимальную работу находим по уравнению (2.24):

А ₌ q(T₁ – T₂/T₁);

A = 8374 • (373 – 303)/373 = 1571 (Дж)

Согласно уравнению (2.25)

η = ;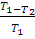

η ₌ 373-303/373 ₌ 0,1875, или 18,75 %

2. При временном контакте тела с температурой 200 °С с телом, нагретым до 100 °С, перешло 418,7 Дж теплоты. Найти общее изме­нение энтропии системы.

Решение. Изменение энтропии теплоотдатчика и теплоприемника находим по уравнению (2.26):

∆S₁ =q/T;

∆S₁ = -418,7/473 = - 0,885 (Дж)

∆S₂ = 418,7/373 = 1,122 (Дж)

Находим общее изменение энтропии:

∆S = ∆S₁ +∆S₂; ∆S = -0,885+1,122 = 0,237 (Дж)

3. Азот объемом 0,001 м³ смешан с кислородом объемом 0,002 м³ при 27 °С и давлении 1,013 • 10⁵ Па. Найти общее изменение энтро­пии системы.

Решение. При смешении газы будут диффундировать друг в друга. Межмолекулярным взаимодействием газов можно пренеб­речь, так как при данных условиях газы можно принять за идеаль­ные. Поэтому общее изменение энтропии при смешении газов будет равно сумме изменений энтропий каждого газа при его расширении до объема смеси. Так как процесс изотермический, то из уравне­ния (1.28) для каждого газа

Из уравнения (1.8) n =pv/RT;

n(N₂) = 0,001•1,013•10⁵ = 0,0405;

n(O₂) = 0,002•1,013•10⁵/8,314•300 = 0,081;

∆S(N₂) = 0,0405 • 8,314 • 2,3lg(0,003/0,001) = 0,371 (Дж)

∆S(O₂) = 0,081• 8,314 • 2,3lg(0,003/0,002) = 0,274 (Дж)

∆S = 0,371 + 0,274 = 0,645 (Дж)

Эта задача может быть решена и по уравнению (2.29), нужно только по уравнению (2.11б) найти парциальные давления газов:

p(N₂) = p_об ;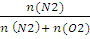

p(N₂) = 1,013 • 10⁵ +0,0405/0,0405 + 0,081 = 0,337 * 10⁵ (Па);

p(O₂) = 1.013•10⁵ – 0,337•10⁵=0,676•10⁵ (Па);

∆S(N₂) = 0,0405•8,314•2,3lg(1,013•10⁵/0,337•10⁵)=0,371 (Дж);

∆S(O₂) = 0,081•8,314•2,3lg(1,013•10⁵/0,676•10⁵)=0,274 (Дж);

∆S = 0,371+0,274=0,645 (Дж);

4. Вода массой 1 кг, взятая при 0 °С, переведена в состояние перегретого пара с температурой 200 °С и давлением 101,3 кПа. Вычислить изменение энтропии этого перехода, если удельная теп­лота испарения воды при 100 °С равна 2257 Дж/г, удельная тепло­емкость воды равна 4,187 Дж (г•К), а удельная теплоемкость водяного пара при давлении в 1,013 • 10⁵ Па равна 1,968 Дж (г•К).

Решение. Общее изменение энтропии будет складываться из трех составляющих: изменения энтропии ∆S₁ при нагревании воды до температуры кипения, изменения энтропии ∆S₂ при пере­ходе воды из жидкого состояния в парообразное и, наконец, изме­нения энтропии ∆S₃ при нагревании сухого пара от 100 до 200 °С: ∆S = ∆S₁+∆S₂ + ∆S₃

∆S₁ определяем по уравнению ∆S = пС_р • 2,3lg(T₂/T₁) —. Оно получено из уравнения (II, 31), если предположить, что система под­чиняется законам для идеальных газов и что объем воды при на­гревании не изменяется. Молярная теплоемкость С_р равна удель­ной теплоемкости, умноженной на молярную массу: С_р = 4,187 • 18 = 75,4 (Дж/(моль • К);

п (Н₂0) = 1000 : 18 = 55,6 моль;

∆S₁ = 55,6 • 75,4 • 2,3lg(373/273) = 1305,5 (Дж)

∆S₂ находим по уравнению (II, 27). Молярная теплота испаре­ния равна:

∆H_исп = 2256,7 • 18 = 40 620 (Дж/моль);

∆S_{2 =} ∆H_исп/T; ∆S_{2 =} 55,6 • 40 620/373 _{= 6065} (Дж)

При нагревании сухого пара от 100 до 200 °С при постоянном давлении изменение энтропии равно: ∆S₃ = пС_р • 2,3lg(T₂/T₁). Молярная теплоемкость пара С_р = 1,968 • 18 = 35,42 (Дж/моль).

∆S₃ = 55,6 • 35,42 • 2,3lg(473/373) = 464,3 (Дж);

∆S = 1303,5 + 6055 + 464,3 = 7824,8 (Дж)

Дата добавления: 2014-10-14; просмотров: 1029; Нарушение авторских прав

Мы поможем в написании ваших работ!