
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Раздел 3. Множественная регрессия
Темы 3.1, 3.2. Линейная модель множественной регрессии. Оценка качества модели множественной регрессии.
Решение типовых задач
Задача 1. Уравнение регрессии, построенное по 17 наблюдениям, имеет вид:
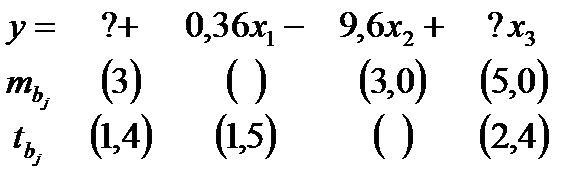
Задание: расставить пропущенные значения, а также построить доверительный интервал для b2 с вероятностью 0,99.
Решение: Пропущенные значения определяем с помощью формулы:
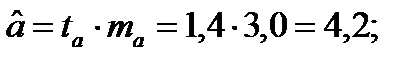
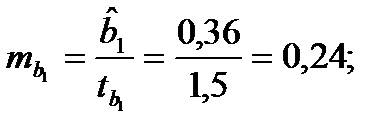
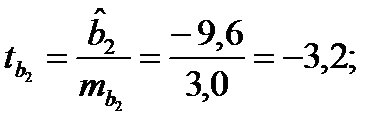
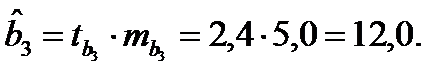
Таким образом, уравнение регрессии со статистическими характеристиками выглядит так:
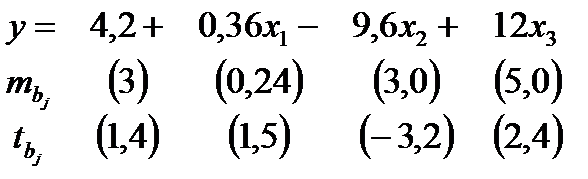
Доверительный интервал для b2 строим по формуле (24). Здесь уровень значимости равен 0,01, а число степеней свободы равно n – p – 1 = 17 – 3 – 1 = 13, где n = 17 – объём выборки, p = 3 – число факторов в уравнении регрессии. Отсюда 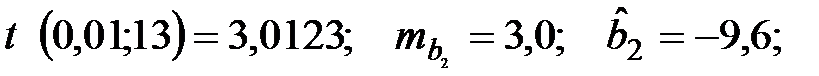
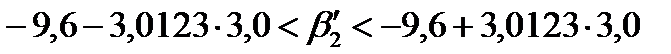 ,или
,или 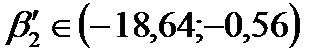 . Этот доверительный интервал накрывает истинное значение параметра
. Этот доверительный интервал накрывает истинное значение параметра 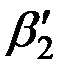 с вероятностью, равной 0,99.
с вероятностью, равной 0,99.
Задача 2. Уравнение регрессии в стандартизованных переменных выглядит так: 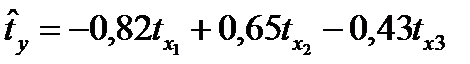 .
.
При этом вариации всех переменных равны следующим величинам:
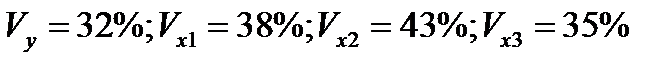 .
.
Задание: сравнить факторы по степени влияния на результирующий признак и определить значения частных коэффициентов эластичности.
Решение: Стандартизованные уравнения регрессии позволяют сравнивать факторы по силе их влияния на результат. При этом, чем больше по абсолютной величине коэффициент при стандартизованной переменной, тем сильнее данный фактор влияет на результирующий признак. В рассматриваемом уравнении самое сильное воздействие на результат оказывает фактор х1, имеющий коэффициент – 0,82, самое слабое – фактор х3 с коэффициентом, равным – 0,43.
В линейной модели множественной регрессии обобщающий (средний) коэффициент частной эластичности определяется выражением, в которое входят средние значения переменных и коэффициент при соответствующем факторе уравнения регрессии натурального масштаба. В условиях задачи эти величины не заданы. Поэтому воспользуемся выражениями для вариации по переменным: 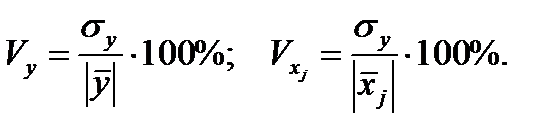
Коэффициенты bj связаны со стандартизованными коэффициентами βj соотношением (15), которое подставим в формулу:
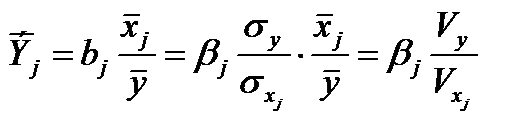 .
.
При этом знак коэффициента эластичности будет совпадать со знаком βj: 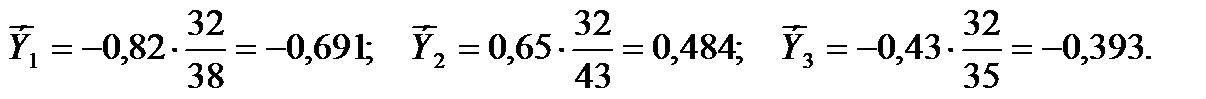
Задача 3. По 32 наблюдениям получены следующие данные:
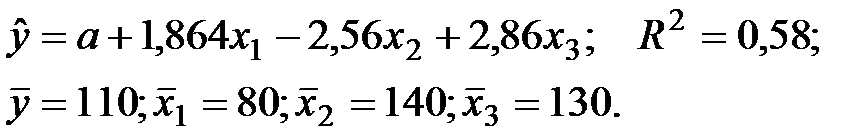
Задание: определить значения скорректированного коэффициента детерминации, частных коэффициентов эластичности и параметра а.
Решение: Значение скорректированного коэффициента детерминации определим по одному из равенств (27):
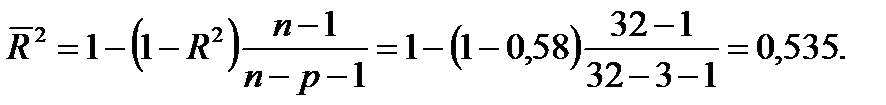
Частные коэффициенты эластичности (средние по совокупности) вычисляем по формулам (19):
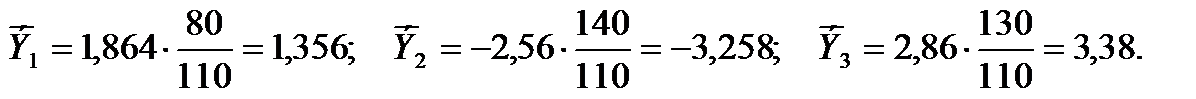
Поскольку линейное уравнение множественной регрессии выполняется при подстановке в него средних значений всех переменных, определяем параметр а (уравнение (17)):
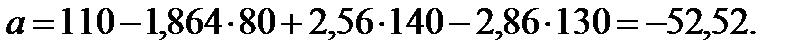
Задача 4. По некоторым переменным имеются следующие статистические данные: 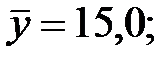
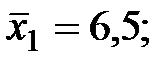
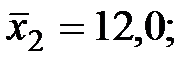
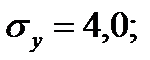
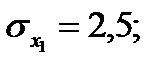
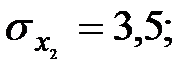
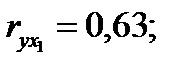
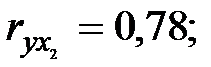
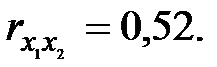
Задание: построить уравнение регрессии в стандартизованном и натуральном масштабах.
Решение: Поскольку изначально известны коэффициенты парной корреляции между переменными, начать следует с построения уравнения регрессии в стандартизованном масштабе. Для этого надо решить систему нормальных уравнений (14), которая в случае двух факторов имеет вид:
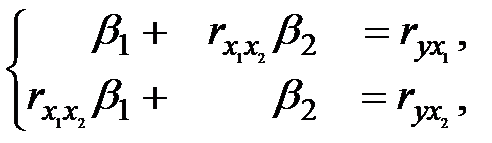
или, после подстановки исходных данных:
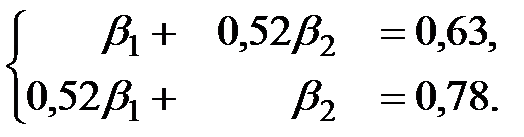
Решаем эту систему любым способом, получаем: β1 = 0,3076, β2 = 0,62.
Запишем уравнение регрессии в стандартизованном масштабе:
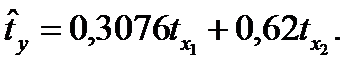
Теперь перейдем к уравнению регрессии в натуральном масштабе, для чего используем формулы:
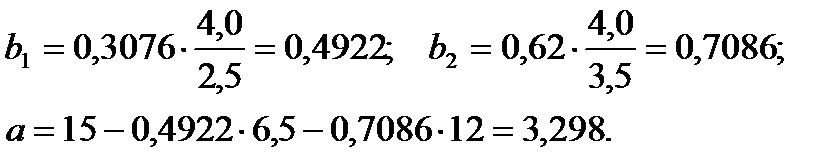
Уравнение регрессии в натуральном масштабе имеет вид:
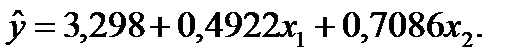
Задача 5. При построении линейной множественной регрессии 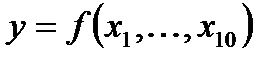 по 48 измерениям коэффициент детерминации составил 0,578. После исключения факторов х3, х7 и х8 коэффициент детерминации уменьшился до 0,495.
по 48 измерениям коэффициент детерминации составил 0,578. После исключения факторов х3, х7 и х8 коэффициент детерминации уменьшился до 0,495.
Задание: Обоснованно ли было принятое решение об изменении состава влияющих переменных на уровнях значимости 0,1, 0,05 и0,01?
Решение: Пусть 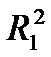 - коэффициент детерминации уравнения регрессии при первоначальном наборе факторов,
- коэффициент детерминации уравнения регрессии при первоначальном наборе факторов, 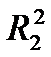 - коэффициент детерминации после исключения трех факторов. Выдвигаем гипотезы:
- коэффициент детерминации после исключения трех факторов. Выдвигаем гипотезы:
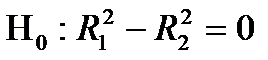 ;
; 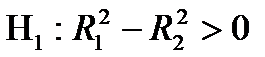
Основная гипотеза предполагает, что уменьшение величины 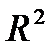 было несущественным, и решение об исключении группы факторов было правильным. Альтернативная гипотеза говорит о правильности принятого решения об исключении.
было несущественным, и решение об исключении группы факторов было правильным. Альтернативная гипотеза говорит о правильности принятого решения об исключении.
Для проверки нуль – гипотезы используем следующую статистику:
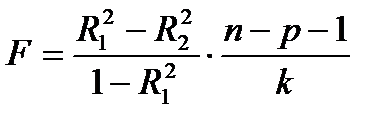 ,где n = 48, p = 10 – первоначальное количество факторов, k = 3 – количество исключаемых факторов. Тогда
,где n = 48, p = 10 – первоначальное количество факторов, k = 3 – количество исключаемых факторов. Тогда 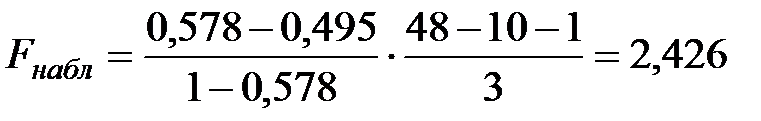
Сравним полученное значение с критическим F(α; 3; 39) на уровнях 0,1; 0,05 и 0,01:
F(0,1; 3; 37) = 2,238;
F(0,05; 3; 37) = 2,86;
F(0,01; 3; 37) = 4,36.
На уровне α = 0,1 Fнабл > Fкр, нуль – гипотеза отвергается, исключение данной группы факторов не оправдано, на уровнях 0,05 0,01 нуль – гипотеза не может быть отвергнута, и исключение факторов можно считать оправданным.
Задача 6. По совокупности 30 предприятий концерна изучается зависимость прибыли y (млн. руб.) от выработки продукции на одного работника x1 (ед.) и индекса цен на продукцию x2 (%). Данные приведены в таблице:
| Признак | Среднее значение | Среднее квадратическое отклонение | Линейный коэффициент парной корреляции |
| у | ryx1=0,68 | ||
| x1 | ryx2=0,63 | ||
| x2 | rx1x2=0,42 |
Задание:
1. Постройте уравнение множественной регрессии в стандартизованной и натуральной форме.
2. Определите показатели частной и множественной корреляции.
3. Найдите частные коэффициенты эластичности и сравните их с β-коэффициентами.
Решение:
1. Линейное уравнение множественной регрессии y от x1 и x2 имеет вид: y=a+b1*x1+b2*x2+e. Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе: ty=β1*tx1+β2*tx2.
Расчет β-коэффициентов выполним по формулам:
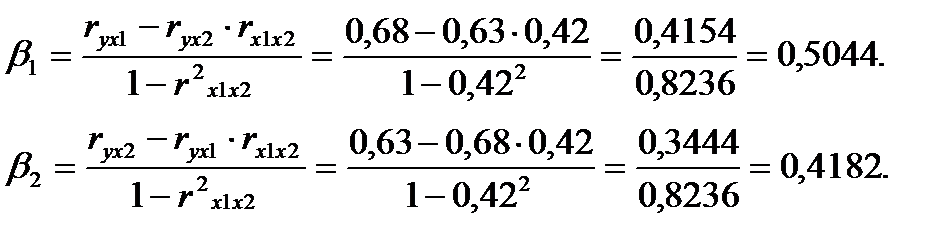

Получим уравнение 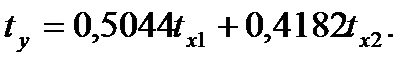
Для построения уравнения в натуральной форме рассчитаем b1 и b2, используя формулы для перехода от βi к bi:
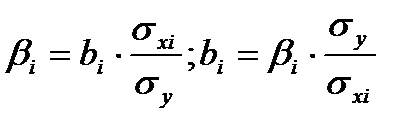
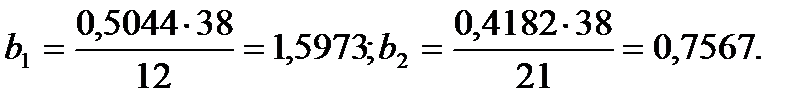
Значение a определим из соотношения:
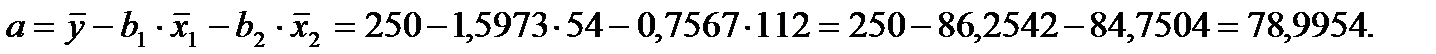
Получим уравнение: y=79,00+1,60*x1+0,76*x2+e.
2. Линейные коэффициенты частной корреляции рассчитываются по рекуррентной формуле:
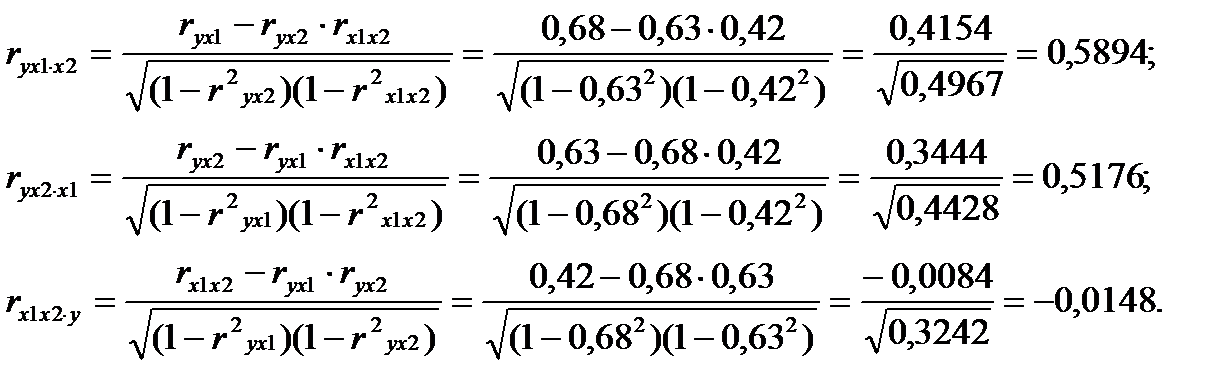
Если сравнить значения коэффициентов парной и частной корреляции, то приходим к выводу, что из-за умеренной межфакторной связи (rx1x2=0,42) коэффициенты парной корреляции оказались завышены.
Расчет линейного коэффициента множественной корреляции выполним по формуле:
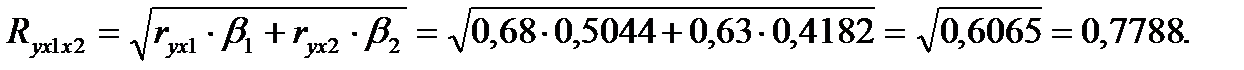
Зависимость y от x1 и x2 характеризуется как тесная, в которой 61% вариации прибыли определяются вариацией выработки продукции и индекса цен на продукцию. Прочие факторы, не включенные в модель, составляют соответственно 39% от общей вариации y.
Общий F-критерий проверяет гипотезу о статистической значимости уравнения регрессии и показателя тесноты связи:
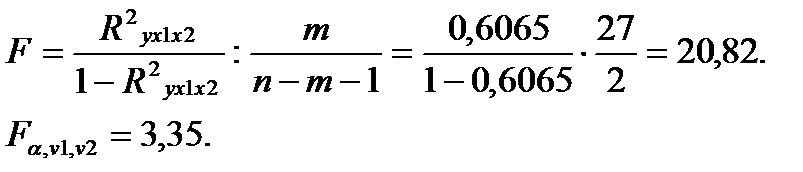
Сравнивая 20,82>3,35, с вероятностью 1-α=0,95 делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи Ryx1x2, которые сформировались под неслучайным воздействием факторов x1 и x2.
3. Для характеристики относительной силы влияния x1 и x2 на y рассчитаем частные коэффициенты эластичности.
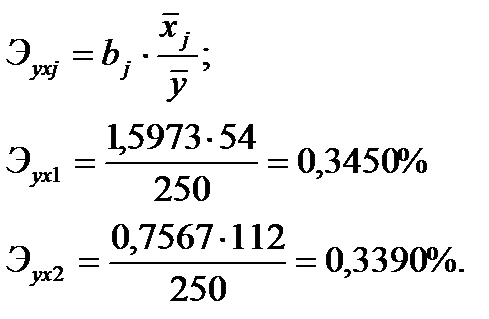
С увеличением выработки продукции одним работником х1 на 1% от ее среднего уровня прибыль y возрастает на 0, 35% от своего среднего уровня; при повышении индекса цен х2 на 1% прибыль возрастает на 0,34% от своего среднего уровня. Очевидно, что сила влияния выработки на размер прибыли немного выше, чем индекса цен. К аналогичным выводам о силе влияния факторов приходим при сравнении модулей значений β1 и β2.
| <== предыдущая страница | | | следующая страница ==> |
| | |
Дата добавления: 2014-10-17; просмотров: 667; Нарушение авторских прав

Мы поможем в написании ваших работ!