
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ОСНОВЫ ТЕОРИИ ИНФОРМАЦИИ
5.1. Предмет и содержание теории информации
Основой процессов управления и связи в технических системах является передача, хранение и преобразование информации. Под информацией понимают совокупность сведений о той или иной физической системе, явлении или событии. Передача информации обеспечивает процесс общения между ее отправителем и получателем, которые, как правило, разделены пространством и временем (рис.5.1).
| Канал связи |
| Источник сообщений |
| Передающее (кодирующее) устройство |
| Приемное (декодирующее) устройство |
| Получатель |
| Источник помех |
Рис. 5.1 - Структурная схема передачи информации
Информация представляет собой свойство материи и требуется материальный носитель, на котором она отображалась бы. В качестве носителей информации могут служить различные объекты, например, листы бумаги, магнитофонные ленты, ферритовая матрица памяти ЦВМ, световые колебания, радиоколебания и т.д.
Отображение информации на носителе означает изменение его состояния по определенным законам.
Отметим, что процесс изменения состояния носителя является процессом формирования сигнала. Это означает, что в качестве сигналов, выступают не сами объекты, а их состояния.
Итак, сигнал, являясь носителем информации, представляет собой изменение по заранее установленному правилу состояния материального объекта.
Сообщения, подлежащие передаче, могут быть дискретными (например, передача текста, состоящего из отдельных букв) или непрерывными (речь, музыка).
Получатель должен быть информирован о том, в каком соответствии находятся сообщения и сигналы, сформированные путем кодирования и модуляции. Это необходимое условие, при котором получатель может извлечь информацию из сигнала. При этом сигнал вследствие неопределенности выбора представляется получателю случайной функцией времени.
В условиях неизбежных помех при передаче информации встают важные проблемы передачи по каналу связи максимального количества информации с минимальными искажениями, обнаружения сигналов в шумах, наилучшей фильтрации и другие.
Основными вопросами, которые решает теория информации, являются вопросы осуществления помехоустойчивого кодирования и декодирования, расчета пропускной способности каналов связи оптимальной обработки сигналов, сбора и хранения информации.
5.2. Энтропия как мера неопределенности состояния системы
Вопрос о количественной мере информации наиболее актуальный в теории информации.
На современном этапе развития этой теории отвлекаются от семантической, смысловой стороны информации и характеризуют ее лишь с одной стороны – со стороны неопределенности рассматриваемой физической системы. При этом под получением информации о состоянии некоторой физической системы подразумевают разность между априорной неопределенностью ее состояния и апостериорной (после постановки опыта по изучению ее состояния) неопределенностью. В связи с этим встает вопрос о том, как измерять неопределенность состояния данной физической системы.
Предположим, что система может находиться с равными вероятностями в одном из n состояний 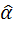 , как показано в табл. 5.1.
, как показано в табл. 5.1.
Таблица 5.1.
Равновероятные состояния системы
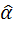
| 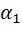
| 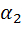
| 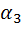
| … | 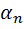
|
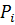
| 
| 
| 
| 
| 
|
Рассмотрим, каким условиям должна удовлетворять функция H ( 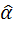 ), характеризующая неопределенность состояния данной системы.
), характеризующая неопределенность состояния данной системы.
Очевидно, что функция H ( 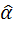 ) должна монотонно возрастать с ростом n, так как интуитивно ясно, что рост количества исходов увеличивает неопределенность. Далее, при отсутствии неопределенности (n = i) функция H (
) должна монотонно возрастать с ростом n, так как интуитивно ясно, что рост количества исходов увеличивает неопределенность. Далее, при отсутствии неопределенности (n = i) функция H ( 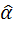 ) должна быть равна нулю.
) должна быть равна нулю.
В итоге, неопределенность состояния совокупности двух и более независимых систем должна быть равна сумме неопределенности состояний отдельных систем (условия аддитивности).
Перечисленным требованиям удовлетворяет логарифмическая функция числа состояния:
H ( 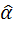 ) =
) = 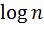 .
.
Выполнение первых двух условий является очевидным.
Для доказательства аддитивности такой меры неопределенности рассмотрим две независимые системы, имеющие n и m исходов соответственно. В этом случае совокупность 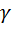 систем будет иметь m и n исходов и после логарифмирования получаем:
систем будет иметь m и n исходов и после логарифмирования получаем:
H ( 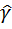 ) =
) =  +
+ 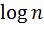 .
.
За единицу неопределенности принимают неопределенность ситуации с двумя равновероятными исходами. Основание логарифма при этом необходимо взять равным двум:
H ( 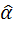 ) =
) = 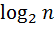 =
= 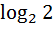 =1.
=1.
Данная единица измерения неопределенности называется двоичной единицей. В зависимости от основания логарифма (e или 10) различают натуральные или десятичные единицы.
Предположим, что система может находиться в n не равновероятных состояниях, как показано в табл. 5.2.
Таблица 5.2
Не равновероятные состояния системы
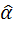
| 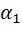
| 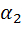
| . . . | 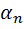
|
P ( 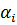 ) )
| P ( 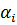 ) )
| P ( 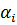 ) )
| . . . | P ( 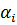 ) )
|
Естественно, что
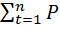 (
( 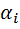 ) = 1 .
) = 1 .
В этом случае неопределенность состояния системы будет зависеть не только от числа состояний n, но и от того, как распределены вероятности состояний.
В этом убеждает рассмотрение двух систем с одинаковым числом состояний, но с разным распределением вероятностей состояний (см. табл. 5.3 и табл. 5.4).
Таблица 5.3
Равновероятные распределения состояний системы
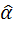
| 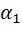
| 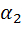
|
P ( 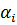 ) )
| 0,5 | 0,5 |
Таблица 5.4
Не равновероятные распределения состояний системы
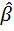
| 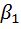
| 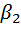
|
P ( 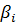 ) )
| 0,999 | 0,001 |
Очевидно, что доопытная неопределенность состояния в первой системе гораздо больше, чем во второй.
Предположим далее, что апостериорная неопределенность равна нулю, то есть после опыта состояние системы становится известным точно. Тогда количество получаемой в результате опыта информации численно равно априорной неопределенности состояния системы.
Количество информации, получаемой в результате опыта, зависит от вероятности наступившего исхода. Действительно, если наступает исход 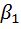 , имеющий вероятность P(
, имеющий вероятность P( 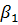 )=0,999, то наблюдатель получит немного информации. Напротив, при наступлении исхода
)=0,999, то наблюдатель получит немного информации. Напротив, при наступлении исхода 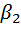 вероятность P(
вероятность P( 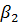 ) = 0,001) наблюдатель получает много информации. Таким образом, можно говорить о том, какое количество информации приходится на каждый конкретный исход опыта, то есть о частной информации.
) = 0,001) наблюдатель получает много информации. Таким образом, можно говорить о том, какое количество информации приходится на каждый конкретный исход опыта, то есть о частной информации.
Частную информацию, получаемую при наступлении 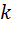 –го исхода опыта можно определить следующим образом:
–го исхода опыта можно определить следующим образом:
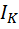 =
= 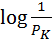 =
= 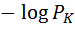 , (5.1)
, (5.1)
здесь 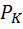 – вероятность к – го исхода опыта. В практике передачи информации пользуются информацией, усреднённой по всем исходам:
– вероятность к – го исхода опыта. В практике передачи информации пользуются информацией, усреднённой по всем исходам:
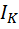 =
= 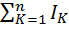
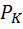 =
= 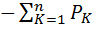
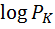 . (5.2)
. (5.2)
Выше было оговорено, что рассматривается случай, когда апостериорная неопределенность состояния системы равна нулю, Поэтому можно полагать, что мерой неопределенности системы с n не равновероятными состояниями следует применять величину
H ( 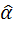 ) =
) = 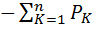
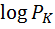 . (5.3)
. (5.3)
Это выражение получило название формула Шеннона.
Подчеркнем, что определяемая формулой (5.3) энтропия – средняя на один исход опыта.
5.3. Энтропия дискретных случайных величин
Считая совокупность различных состояний системы с их вероятностями множеством значений случайной величины с дискретным распределением вероятностей, рассмотрим двумерную дискретную случайную величину со статистическими зависимыми составляющими  и
и  . Будем полагать, что случайная величина
. Будем полагать, что случайная величина  может принимать n значений с соответствующими вероятностями P (
может принимать n значений с соответствующими вероятностями P ( 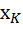 ), к =
), к = 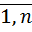 , а случайная величина
, а случайная величина 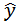 – m значений с вероятностями P (
– m значений с вероятностями P ( 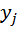 ), j =
), j = 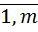 .
.
Составим таблицу возможных сочетаний значений случайных величин  и
и  и соответствующих этим сочетаниям значений вероятностей (табл. 5.5).
и соответствующих этим сочетаниям значений вероятностей (табл. 5.5).
Таблица 5.5
Вероятности сочетаний случайных величин  и
и 
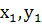 P (
P ( 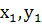 ) )
| 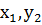 P (
P ( 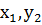 ) )
| . . . | 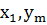 P (
P ( 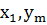 ) )
|
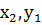 P (
P ( 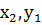 ) )
| 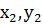 P (
P ( 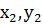 ) )
| . . . | 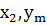 P (
P ( 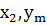 ) )
|
| . . . | . . . | . . . | . . . |
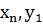 P (
P ( 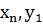 ) )
| 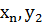 P (
P ( 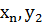 ) )
| . . . | 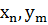 P (
P ( 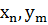 ) )
|
Учитывая (5.3) и на основании данной таблицы записываем выражение для энтропии совокупности случайных величин  ,
,  :
:
H ( 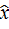 ,
,  ) =
) = 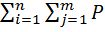 (
( 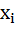 ,
, 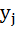 )
) 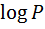 (
( 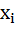 ,
, 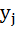 ). (5.4)
). (5.4)
Преобразуем выражение (5.4), используя соотношение
P ( 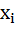 ,
, 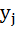 ) = P (
) = P ( 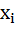 )
) 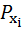 (
( 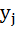 ) :
) :
H(  ,
,  ) =
) = 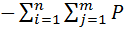 (
( 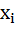 )
) 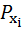 (
( 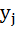 )
)  =
=
= 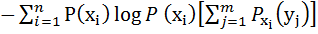 + +
+ +  .
.
Первое слагаемое в этом выражении есть энтропия H (  ), так как
), так как 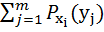 =1 .
=1 .
Во втором слагаемом величина
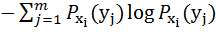 =
= 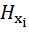 (
(  )
)
представляет собой энтропию величины  при условии, что случайная величина
при условии, что случайная величина  приняла конкретное значение
приняла конкретное значение 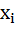 .
.
Условная энтропия величины  , усредненная по всем возможным значениям случайной величины
, усредненная по всем возможным значениям случайной величины  , называется полной условной энтропией случайной величины
, называется полной условной энтропией случайной величины  относительно случайной величины
относительно случайной величины  :
:
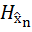 (
(  ) =
) = 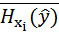 =
= 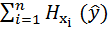
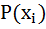 =
=
= 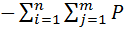 (
( 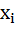 )
) 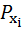 (
( 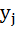 )
) 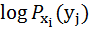 . (5.5)
. (5.5)
Таким образом,
H (  ,
,  ) = H(
) = H(  ) +
) + 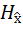 (
(  ) . (5.6)
) . (5.6)
Можно также показать справедливость следующего равенства:
H (  ,
,  ) = H (
) = H (  ) +
) + 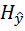 (
(  ) . (5.7)
) . (5.7)
Здесь
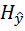 (
(  ) =
) = 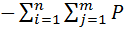 (
( 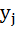 )
) 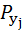 (
( 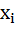 )
) 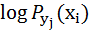 . (5.8)
. (5.8)
Если величины  и
и  статистически независимы, то есть
статистически независимы, то есть
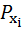 (
( 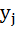 ) =
) = 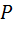 (
( 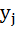 ),
),
то
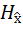 (
(  ) =
) = 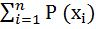
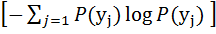 = H(
= H(  ). (5.9)
). (5.9)
Это означает, что условная энтропия равна безусловной и
H (  ,
,  ) = H(
) = H(  ) + H(
) + H(  ). (5.10)
). (5.10)
При жесткой функциональной связи случайных величин  и
и  значение
значение  однозначно определяет значение
однозначно определяет значение  , откуда
, откуда
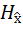 (
(  ) = 0.
) = 0.
Следовательно, в этом случае
H (  ,
,  ) = H(
) = H(  ) .
) .
Можно показать, что в общем случае выполняются следующие неравенства:
0 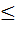
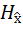 (
(  )
) 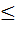 H (
H (  );
);
0 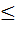
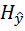 (
(  )
) 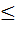 H (
H (  ).
).
Таким образом, статистическая зависимость между случайными величинами, входящими в систему, уменьшает энтропию системы.
Предположим, что производится опыт, в результате которого становится известным значение одной из статистически зависимых случайных величин, например  .
.
При этом неопределенность величины  если не исчезает полностью, то уменьшается. Количество информации
если не исчезает полностью, то уменьшается. Количество информации 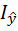 (
(  ) относительно случайной величины
) относительно случайной величины  , получаемой в результате опыта над случайной величиной
, получаемой в результате опыта над случайной величиной  , определяется как убыль энтропии.
, определяется как убыль энтропии.
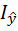 (
(  ) = H (
) = H (  )
) 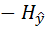 (
(  ). (5.11)
). (5.11)
Выражение (5.11) определяет разность доопытной и оставшейся после опыта неопределенности случайной величины  .
.
В случае независимых случайных величин  и
и  имеем:
имеем:
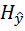 (
(  ) = H (
) = H (  )
)
и
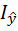 (
(  ) = H (
) = H (  )
)  H (
H (  ) = 0,
) = 0,
то есть знание величины  не уменьшает неопределенности величины
не уменьшает неопределенности величины  . Если случайные величины
. Если случайные величины  и
и  связаны жесткой функциональной зависимостью, то
связаны жесткой функциональной зависимостью, то 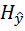 (
(  )=0 и
)=0 и 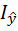 (
(  )=H(
)=H(  ). Очевидно, что выполняется следующее неравенство:
). Очевидно, что выполняется следующее неравенство:
0 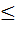
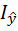 (
(  )
) 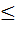 H (
H (  ). (5.12)
). (5.12)
Из уравнений (5.6) и (5.7) следует, что
H (  ) +
) + 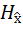 (
(  ) = H (
) = H (  ) +
) + 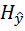 (
(  ),
),
следовательно,
H (  )
) 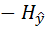 (
(  ) =
) = 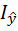 (
(  ) = H (
) = H (  )
) 
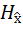 (
(  ) =
) = 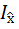 (
(  ).
).
Таким образом, информация о случайной величине  , полученная при наблюдении величины
, полученная при наблюдении величины  , равна информации о случайной величине
, равна информации о случайной величине  , полученной при наблюдении величины
, полученной при наблюдении величины  . Это обстоятельство позволяет ввести для количества информации симметричное обозначение
. Это обстоятельство позволяет ввести для количества информации симметричное обозначение
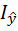 (
(  ) =
) = 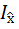 (
(  ) = I (
) = I (  ,
,  ).
).
Выражение (5.11) можно, получить в симметричной относительной  и
и  форме
форме
I (  ,
,  ) =
) = 
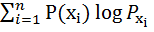 +
+ 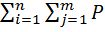 (
( 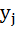 )
) 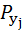 (
( 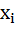 )
) 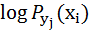 =
=
= 
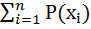
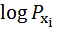 +
+ 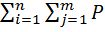 (
( 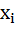 ,
, 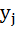 )
) 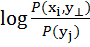 . ⊥j
. ⊥j
Умножив первое слагаемое на
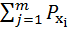 (
( 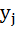 ) =1,
) =1,
найдем
I(  ,
,  ) =
) = 
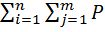 (
( 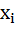 ,
, 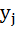 )
) 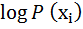 +
+ 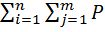 (
( 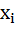 ,
, 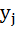 )
) 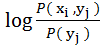 =
=
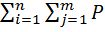 (
( 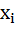 ,
, 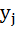 )
) 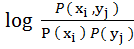 . (5.13)
. (5.13)
5.4. Энтропия дискретных случайных процессов
Ранее рассматривались свойства энтропии дискретных случайных величин. Рассмотрим теперь понятие энтропии применительно к случайным последовательностям некоторых символов (например, цифр, букв). Данный вопрос имеет существенное практическое значение, так как во многих случаях для передачи информации используются дискретные последовательности. Будем в дальнейшем рассматривать так называемые эргодические последовательности, у которых вероятностные связи распространяются на конечное число элементов.
Рассмотрим вначале случай равновероятных статистических независимых элементов случайной последовательности. Предположим, что число различных элементов равно N. Число различных слов длиной S элементов, которые можно составить из алфавита объемом в N элементов, равно
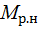 =
= 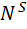 . (5.14)
. (5.14)
Здесь индекс " 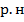 " означает равновероятные независимые элементы. Вследствие независимости и равновероятности элементов, из которых составлены, слова, вероятности их появления одинаковы и равны
" означает равновероятные независимые элементы. Вследствие независимости и равновероятности элементов, из которых составлены, слова, вероятности их появления одинаковы и равны
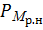 =
= 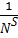 .
.
Отсюда по формуле (5.3) находим среднюю энтропию на одно слово
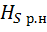 =
= 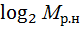 = S
= S 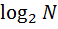 дв. ед.
дв. ед.
Энтропия, приходящаяся на одну букву, равна
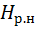 =
= 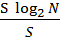 =
= 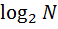 . (5.15)
. (5.15)
Предположим, что элементы случайной последовательности являются не равновероятными и независимыми. Считая длину слова 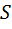 достаточно большой, можно утверждать, что элементы в каждом слове будут встречаться с относительными частостями, весьма близкими к их вероятностям. Количество слов, у которых частость появления элементов существенно отличается от вероятности, будем полагать пренебрежимо малым.
достаточно большой, можно утверждать, что элементы в каждом слове будут встречаться с относительными частостями, весьма близкими к их вероятностям. Количество слов, у которых частость появления элементов существенно отличается от вероятности, будем полагать пренебрежимо малым.
Элемент 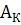 в длинном слове встретится SP(
в длинном слове встретится SP( 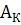 ),
), 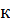 =
= 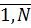 раз, а вероятность этого события равна [ Р(
раз, а вероятность этого события равна [ Р( 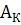 )
) 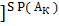 .
.
Следовательно, вероятность появления слова длиной S равна
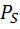 =
= 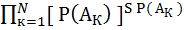 .
.
Общее число различных слов вследствие их равновероятности определяется соотношением
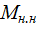 =
= 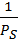 =
= 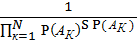 . (5.16)
. (5.16)
Отсюда находим среднюю энтропию на одно слово
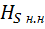 =
= 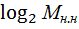 =
= 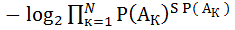 =
=  S
S 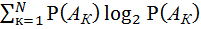 .
.
(5.17)
На один элемент последовательности приходится энтропия, равная
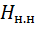 =
= 
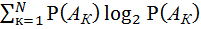 . (5.18)
. (5.18)
Наконец, рассмотрим случай, когда элементы случайной последовательности статистически зависимы. Предположим, что элементы случайной последовательности образуют простую односвязную цепь Маркова, то есть вероятностная связь существует только между двумя соседними элементами и вероятность передачи элемента 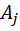 будет зависеть только от того, каким был предшествующий символ
будет зависеть только от того, каким был предшествующий символ  . Зафиксируем предшествующий символ
. Зафиксируем предшествующий символ  и определим энтропию в этом случае:
и определим энтропию в этом случае:
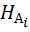 (
( 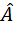 ) =
) = 
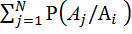
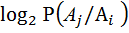 .
.
Усредняя по всем элементам  получим
получим
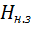 (
( 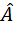 )=
)= 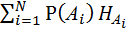 (
( 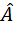 )=
)= 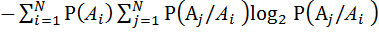 =
=
= 
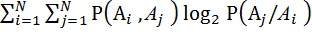 . (5.19)
. (5.19)
Если вероятностные связи имеют место между тремя элементами, то энтропия последовательности, приходящаяся на один элемент, будет равна
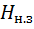 (
( 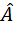 ) =
) = 
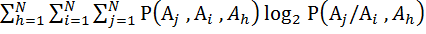 . (5.20)
. (5.20)
При наличии связей между большим числом элементов энтропия подсчитывается аналогичным образом. Вероятностные связи между элементами уменьшают энтропию последовательности и тем интенсивнее, чем теснее эти связи и чем большее число элементов будет ими охвачено.
Рассмотрим пример. Пусть случайная последовательность состоит из элементов 0 и 1, вероятности которых соответственно равны P( 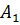 )= 0,6 Р(
)= 0,6 Р( 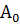 ) = 0,4. Условные вероятности появления любого из символов таковы:
) = 0,4. Условные вероятности появления любого из символов таковы:
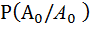 = 0,1 ,
= 0,1 , 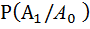 = 0,9 ;
= 0,9 ;
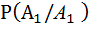 = 0,1 ,
= 0,1 , 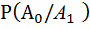 = 0,9 .
= 0,9 .
По формуле (5.19) находим энтропию на один элемент:
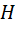 (
( 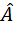 ) =
) = 
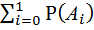
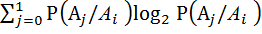 =
=

 (0,1
(0,1 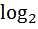 0,1 + 0,9
0,1 + 0,9 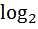 0,9) (0,6 + 0,4) 0,467 дв. ед.
0,9) (0,6 + 0,4) 0,467 дв. ед.
При отсутствии статистических связей между элементами энтропия на один элемент оказалась бы равной
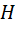 (
( 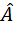 ) =
) = 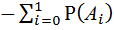
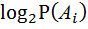 =
=  0,4
0,4 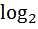 0,4
0,4  0,6
0,6 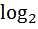 0,6= 0,973 дв. ед.
0,6= 0,973 дв. ед.
Наконец, при равновероятности и независимости элементов последовательности получаем:
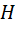 (
( 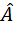 ) =
) =  0,5
0,5 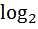 0,5
0,5  0,5
0,5 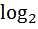 0,5 = 1,0 дв. ед,
0,5 = 1,0 дв. ед,
то есть максимально возможную в данном случае энтропию.
5.5. Энтропия непрерывных случайных величин и сигналов
Выражение, определяющее энтропию непрерывной случайной величины, получим предельным переходом из дискретного варианта.
Заменим непрерывную случайную величину  дискретной случайной величиной
дискретной случайной величиной 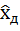 . С этой целью разобьем область возможных значений величины
. С этой целью разобьем область возможных значений величины  на равные интервалы
на равные интервалы  х и произведем ступенчатую аппроксимацию кривой плотности вероятности (рис. 5.2).
х и произведем ступенчатую аппроксимацию кривой плотности вероятности (рис. 5.2).
Рис. 5.2 – Гистограмма распределения величины 
В пределе при  х
х 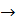 0 от дискретной случайной величины переходим к непрерывной:
0 от дискретной случайной величины переходим к непрерывной:
H ( 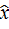 ) =
) = 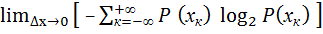 =
=
= 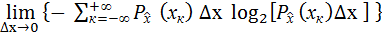 =
=
= 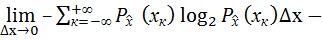
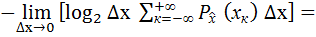
= 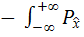 ( x )
( x ) 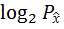 ( x ) dx
( x ) dx 
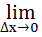
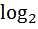
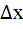 . (5.21)
. (5.21)
С уменьшением интервала 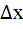 второе слагаемое в (5.21) стремится к бесконечности, что объясняется ростом числа возможных состояний случайной величины и, следовательно, увеличением неопределенности ее состояния.
второе слагаемое в (5.21) стремится к бесконечности, что объясняется ростом числа возможных состояний случайной величины и, следовательно, увеличением неопределенности ее состояния.
В связи с этим используют относительную энтропию
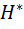 (
(  ) = H (
) = H (  )
)  H (
H ( 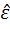 ),
),
где H ( 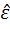 ) – энтропия некоторого стандартного распределения, определяющая начало отсчета энтропии.
) – энтропия некоторого стандартного распределения, определяющая начало отсчета энтропии.
В качестве, энтропии H ( 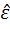 ) обычно выбирают равномерное распределение в единичном интервале
) обычно выбирают равномерное распределение в единичном интервале
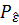 (
( 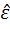 ) =
) = 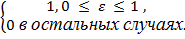
Тогда
H ( 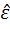 ) =
) = 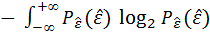 d
d 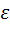

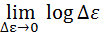 =
= 
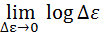 .
.
При 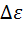 =
= 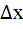 для энтропии непрерывной случайной величины имеем выражение
для энтропии непрерывной случайной величины имеем выражение
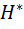 (
( 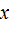 ) =
) = 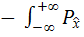 (x)
(x) 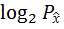 (x)dx . (5.22)
(x)dx . (5.22)
Весьма важным с практической стороны является вопрос о том, какие распределения 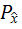 (x) обеспечивают максимальные значения энтропии.
(x) обеспечивают максимальные значения энтропии.
В дальнейшем нам будет необходим следующий результат из вариационного исчисления. Пусть имеется интеграл
I = 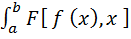 dx, (5.23)
dx, (5.23)
зависящий от вида функции 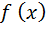 . Требуется найти такую
. Требуется найти такую 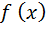 , которая при заданных условиях:
, которая при заданных условиях:
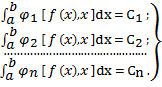 (5.24)
(5.24)
где функции  ,
, 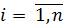 и константы
и константы 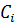 ,
, 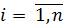 известны, обеспечивает максимум интеграла (5.23).
известны, обеспечивает максимум интеграла (5.23).
Доказано, что такая функция 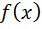 находится из уравнения
находится из уравнения
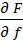 +
+ 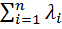
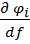 = 0 . (5.25)
= 0 . (5.25)
Здесь 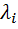 ,
, 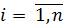 – неопределенные множители Лагранжа.
– неопределенные множители Лагранжа.
Разберем следующие случаи.
1. Случайная величина может принимать значения из интервала (a, b).
Искомое распределение случайной величины должно удовлетворять условию нормировки
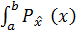 dx = 1 .
dx = 1 .
Воспользовавшись (5.23) – (5.25), записываем для выражения (5.22):
F 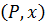 =
= 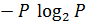 ;
;
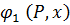 = P,
= P, 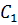 = 1;
= 1;
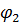 =
= 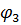 = … =
= … = 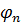 = 0 .
= 0 .
Частные производные имеют вид:
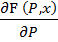 =
= 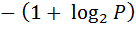 ;
;
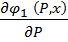 = 1 .
= 1 .
Уравнение (5.25) в данном случае приобретает вид:
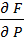 +
+ 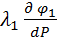 =
= 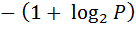 +
+ 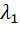 ,
,
откуда
P = 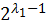 .
.
Для нахождения множителя 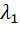 используем условия нормировки:
используем условия нормировки:
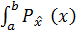 dx =
dx = 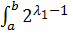 dx =
dx = 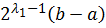 = 1 .
= 1 .
Следовательно, 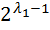 =
=  ;
;
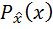 =
= 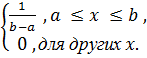
Таким образом, равномерный закон распределения обладает наибольшей энтропией среди всех законов с одним и тем же интервалом значений случайной величины.
2. Случайная величина имеет фиксированную дисперсию (интервал возможных значений 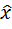 не ограничивается):
не ограничивается):
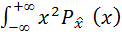 dx =
dx = 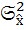 = const. (5.26)
= const. (5.26)
Здесь имеем:
F 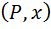 =
= 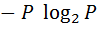 ;
; 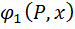 = P;
= P; 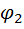 =
= 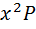 ;
;
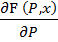 =
= 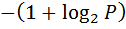 ;
; 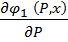 =1;
=1; 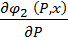 =
= 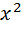 ;
;
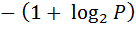 +
+ 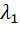 +
+ 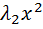 = 0,
= 0,
откуда
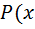 ) =
) =  .
.
Неопределенные множители 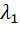 и
и 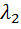 находим из уравнений:
находим из уравнений:
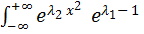 dx = 1;
dx = 1; 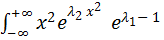 =
= 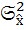 .
.
Проделав несложные подстановки и выполнив интегрирование, находим
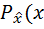 ) =
) =  exp
exp 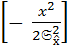 .
.
Следовательно, из всех законов с заданной дисперсией нормальный закон имеет максимальную энтропию.
Рассмотрим задачу о нахождении энтропии непрерывного случайного процесса.
В соответствии с теоремой Котельникова непрерывная случайная функция времени с ограниченным спектром может быть представлена совокупностью дискрет, отстоящих друг от друга на 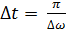 , где
, где 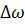 – ширина энергетического спектра случайного процесса.
– ширина энергетического спектра случайного процесса.
На конечном интервале времени Т число выборочных значений равно n = 
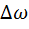 .Эти значения в общем случае статистически связаны друг с другом и представляют собой n – мерную непрерывную случайную величину, характеризующуюся совместной плотностью вероятности
.Эти значения в общем случае статистически связаны друг с другом и представляют собой n – мерную непрерывную случайную величину, характеризующуюся совместной плотностью вероятности
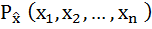 .
.
Отсюда энтропия непрерывного случайного процесса определяется выражением
H 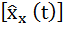 =
= 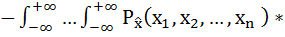
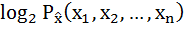 d
d 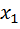 d
d  … d
… d 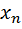 . (5.27)
. (5.27)
Если дискреты не коррелированы и независимы, как в случае "белого" гауссовского шума, то энтропия его будет равна сумме энтропий отдельных дискрет.
Средняя энтропия на реализацию "белого" гауссовского шума длиной Т, равна
H 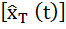 =
= 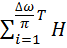 (
( 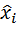 ) =
) = 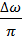 TH (
TH ( 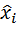 ).
).
Можно показать, что энтропия 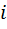 – й дискрет H (
– й дискрет H ( 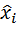 ) для нормального распределения определяется выражением
) для нормального распределения определяется выражением
H ( 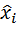 ) =
) = 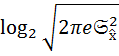 .
.
Тогда
H 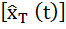 =
= 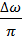 T
T 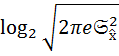 .
.
Как видно из последнего выражения, с увеличением скорости флюктуаций (ширины спектра 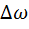 ) энтропия случайного процесса растет.
) энтропия случайного процесса растет.
| <== предыдущая страница | | | следующая страница ==> |
| ЭГРЕГОРЫ | | | РАЗДЕЛ 6 ТЕХНИКО-ЭКОНОМИЧЕСКИЕ РАСЧЁТЫ |
Дата добавления: 2014-10-17; просмотров: 508; Нарушение авторских прав

Мы поможем в написании ваших работ!