
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
РАЗДЕЛ III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
§1.АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
5.1. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору
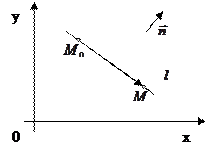 Пусть
Пусть 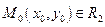 ,
,  .
.
Найти: уравнение прямой 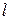 , проходящей через точку
, проходящей через точку 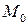 перпендикулярно вектору
перпендикулярно вектору 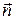 (см. рис.)
(см. рис.)
Назовем 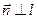 _____________________________.
_____________________________.
Выберем на 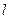 произвольную точку
произвольную точку 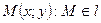 .
.
Найдем координаты  . Т.к.
. Т.к. 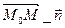 , то ___________
, то ___________ 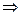
| (5.1) |
– уравнение прямой 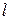 , ___________________________________________
, ___________________________________________
__________________________________________________________
5.2. Общее уравнение прямой
Из уравнения 5.1 с помощью элементарных преобразований получим:
_________________________________________________________________
(5.2)
– ____________________________________.
Частные случаи уравнения (5.2)
1) _____________, 2) ______________, 3) ______________, 4) ____________,
5) __________________.
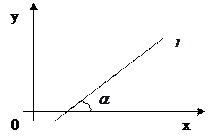 5.3. Уравнение прямой с угловым коэффициентом
5.3. Уравнение прямой с угловым коэффициентом
Пусть 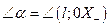 . Разрешим общее уравнение прямой (5.2) относительно
. Разрешим общее уравнение прямой (5.2) относительно 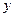 : ___________
: ___________ 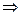
 . Пусть ____________, тогда
. Пусть ____________, тогда
_________________________________________ (5.3)
где ___ – угловой коэффициент прямой, _____ – отрезок, который отсекает данная прямая на оси 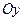 .
.
Замечание 1. Если _____, то _____ – прямая проходит ______________ _________________; если _____, то ______ – семейство прямых, ___________________________________________
5.4. Параметрические и канонические уравнения прямой
Определение 5.1
Всякий ___________вектор 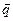 ________________ прямой
________________ прямой 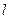 называется ______________________________ этой прямой.
называется ______________________________ этой прямой.
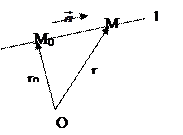 Пусть точка
Пусть точка 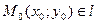 , тогда произвольная точка
, тогда произвольная точка 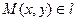 лишь при условии, когда вектор
лишь при условии, когда вектор 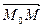 ____________
____________ 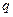 . Это означает, что ________________
. Это означает, что ________________
Если обозначить радиус-вектора точек 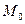 ,
, 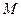 через __ и __, соответственно, то
через __ и __, соответственно, то 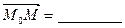 , тогда:
, тогда:
____________
Если ______________________________, то в координатах запишется:
| (5.4) |
– ______________________ прямой на плоскости, проходящей через точку _________ в направлении _______________.
Исключая из уравнений (5.4) параметр __, получаем:
| (5.5) |
– ______________________________ прямой.
Замечание 2. Уравнение (5.5) необходимо воспринимать как ________________: если ____, то это прямая, ______________________, проходящая через точку ______.
Замечание 3.
Приведем уравнение (5.5) к общему знаменателю:
________________________________________
– общее уравнение прямой.
1) В задачах ______ часто обозначают __________.
2) __________________________________________________________ ______________
Вместе с каноническим уравнением (5.5) используется уравнение прямой, _______________________________: если 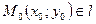 ,
, 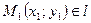 , то
, то
 .
.
Можно в качестве _________________ вектора принять __________, тогда:
| (5.6) |
– уравнение прямой, ______________________________________________.
5.5. Уравнение прямой в отрезках
Пусть дано общее уравнение прямой: _______________________________
Тогда
| (5.7) | __________________________________________ |
– ____________________________, где 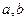 – _______________________ ____________________________________________________________.
– _______________________ ____________________________________________________________.
Пример 5.1. Построить прямую, заданную общим уравнением 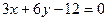 . Написать уравнение этой прямой в отрезках.
. Написать уравнение этой прямой в отрезках.
Ответ.
5.6. Взаимное расположение прямых на плоскости
Утверждение 5.1. Для того чтобы прямые 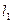 и
и 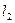 , заданные уравнениями
, заданные уравнениями
(5.8)
_____________________, необходимо и достаточно, чтобы
Утверждение 5.2.Прямые 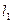 и
и 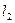 , заданные уравнениями (5.8) _______________________________ тогда и только тогда, когда
, заданные уравнениями (5.8) _______________________________ тогда и только тогда, когда
Замечание 4. _________________________________________________
5.7. Полярная система координат. Расстояние от точки до прямой
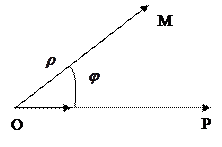 Зафиксируем на плоскости точку
Зафиксируем на плоскости точку 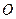 и назовем ее _____________. Луч
и назовем ее _____________. Луч 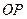 , исходящий из __________, назовем ___________________. Выберем масштаб для измерения длин отрезков и условимся, что поворот вокруг т.
, исходящий из __________, назовем ___________________. Выберем масштаб для измерения длин отрезков и условимся, что поворот вокруг т. 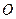 __________________ будем считать __________________. Рассмотрим любую точку
__________________ будем считать __________________. Рассмотрим любую точку 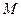 на заданной плоскости, обозначим через __ ее расстояние до полюса и назовем __________________. Угол, на который нужно повернуть полярную ось
на заданной плоскости, обозначим через __ ее расстояние до полюса и назовем __________________. Угол, на который нужно повернуть полярную ось 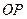 , чтобы она совпала с
, чтобы она совпала с 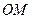 обозначим через __ и назовем ______________________.
обозначим через __ и назовем ______________________.
Определение 5.2
__________________________ точки 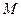 называется ее __________________ _________________________________________________________________
называется ее __________________ _________________________________________________________________
Рассмотрим декартовую прямоугольную систему координат: полюс совпадает с началом, а полярная ось – с положительной полуосью 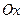 . Здесь
. Здесь 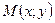 . Тогда:
. Тогда:
| (5.9) |
– формулы связи между прямоугольной декартовой и полярной системами координат.
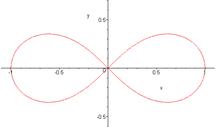 Пример 5.2.
Пример 5.2. 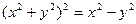 – уравнение лемнискаты Бернулли. Записать его в полярной системе координат.
– уравнение лемнискаты Бернулли. Записать его в полярной системе координат.
(5.10)
– формула нахождения расстояния от произвольной точки 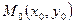 до прямой, заданной уравнением __________________________
до прямой, заданной уравнением __________________________
5.8. Угол между двумя прямыми
Пусть даны две прямые: ____________________. Тогда
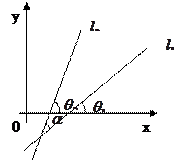
 (5.11)
(5.11)
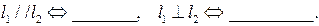
5.9. Кривые второго порядка
Рассмотрим алгебраическое уравнение второй степени относительно 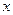 и
и 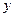 :
:
| (5.12) |  , ,
|
где 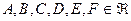 ,
, 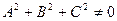 , т.е.
, т.е. 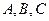 одновременно не равны
одновременно не равны 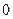 .
.
Уравнение (5.12) определяет _____________________________________.
5.9.1. Окружность
Определение 5.3
Геометрическое место точек, _________________ от одной точки, называемый __________, называется _________________________.
На плоскости выберем точку 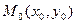 , тогда если
, тогда если 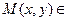 окружности, то
окружности, то
 или
или
| (5.13) |
Если 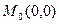 , то
, то
| (5.13’) |
– __________________________________ уравнение окружности.
Замечание 5. Если 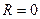 , то окружность стягивается в точку
, то окружность стягивается в точку 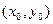 . Если в правой части уравнения (5.13) (
. Если в правой части уравнения (5.13) ( 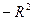 ), то уравнение определяет мнимую окружность.
), то уравнение определяет мнимую окружность.
Равенство (5.12) определяет окружность, если
________________. (*)
Чтобы уравнение (5.12) при условии (*) привести к каноническому виду (5.13), необходимо ___________________________________ относительно 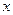 и
и 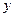 .
.
Пример 5.3. Уравнение окружности 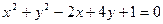 привести к каноническому виду.
привести к каноническому виду.
Решение.
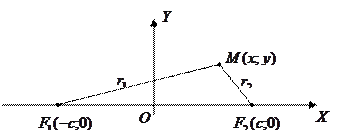 5.9.2. Эллипс
5.9.2. Эллипс
Определение 5.4
Геометрическое место точек, для каждой из которых __________________ до двух данных точек 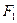 и
и 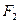 , называемых его _____________, есть величина ____________________, называется __________________.
, называемых его _____________, есть величина ____________________, называется __________________.
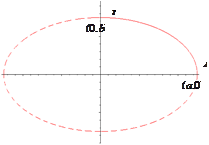 Отметим на оси
Отметим на оси 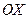 две точки:
две точки: 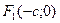 ,
, 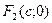 т.е.
т.е. 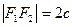 (___________ __________________). Пусть
(___________ __________________). Пусть 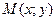 - произвольная точка эллипса.
- произвольная точка эллипса.
________________________ ( 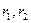 ) точки
) точки 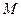 эллипса называются ____________________ ____________________________________________
эллипса называются ____________________ ____________________________________________
_______________________
| (5.14) |
– ______________________________________
Отрезок 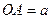 называется ____________________, отрезок
называется ____________________, отрезок 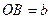 называется ____________________.
называется ____________________.
Замечание 6. Уравнение (5.14) можно рассматривать и в случае ________, тогда 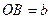 - _______________ и фокусы эллипса ___________________
- _______________ и фокусы эллипса ___________________
Замечание 7. В случае, когда ___________, уравнение (5.14) вырождается в ________________с центром в ______________________________________
Если центр эллипса перенести в точку 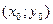 , то уравнение эллипса примет вид:
, то уравнение эллипса примет вид:
Замечание 8. Уравнение __________ определяет ____________ эллипс.
Уравнение ____________ определяет ______________.
Алгебраическое уравнение (5.12) определяет эллипс, если
____________. (**)
Пример 5.4. Уравнение эллипса 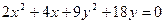 привести к каноническому виду.
привести к каноническому виду.
Решение.
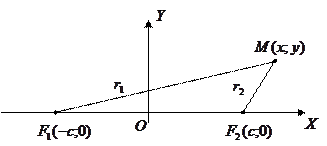 5.9.3. Гипербола
5.9.3. Гипербола
Определение 5.5
Геометрическое место точек, абсолютная величина __________ каждой из которых до двух данных точек 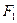 и
и 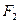 , называемых его фокусами, есть величина _______________, и называется ____________________, т.е.
, называемых его фокусами, есть величина _______________, и называется ____________________, т.е.
(5.15)
– _______________________________
– _________________________________
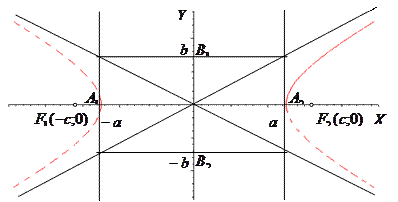 При построении гиперболы необходимо построить прямоугольник со сторонами __ и __ и провести диагонали, которые и являются __________ (см. рис.).
При построении гиперболы необходимо построить прямоугольник со сторонами __ и __ и провести диагонали, которые и являются __________ (см. рис.).
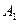 ,
, 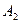 – _______________,
– _______________, 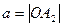 – ____________________,
– ____________________, 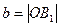 – _________________,
– _________________, 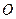 – ________________________.
– ________________________.
Если _____, то гипербола называется ___________________, ее уравнение имеет вид:
Замечание 8. Уравнение
(5.16)
определяет гиперболу ______________________________
Гиперболы, определяемые уравнениями (5.15) и (5.16), называются __________________________
Если центр гипербол перенести в точку 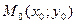 , то уравнение примет вид:
, то уравнение примет вид:
Замечание 9. Уравнение ___________ определяет ___________________
Можно выяснить при каких коэффициентах уравнение (5.12) будет определять гиперболу или семейство прямых. По аналогии с эллипсом в уравнении (5.12)
__________________ (***)
5.9.4. Парабола
Определение 5.6
______________ называется геометрическое место точек, равноудаленных ___________, называемой _____________ и точки, называемой _________
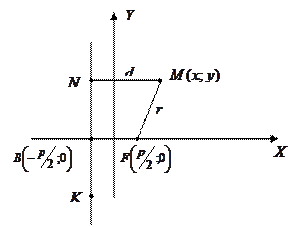
Пусть дано: ______________________________________
(5.17)
– _________________________________________
Здесь ____________________________________________________________ _____________________________________________________________
Если фокус параболы расположен ____________, то уравнение будет иметь вид: ____________.
– _____________________________________________
Замечание 10. Частные случаи: а) _________________________________
б) ______________________________________________
в) ______________________________________________
Уравнение (5.12) определяет параболу, если ____________. (****)
| <== предыдущая страница | | | следующая страница ==> |
| | | Учебно-методическое и информационное обеспечение математических дисциплин |
Дата добавления: 2014-10-17; просмотров: 429; Нарушение авторских прав

Мы поможем в написании ваших работ!