Глава 2. Основы алгоритмизации

2.1. Понятие алгоритма

Понятие алгоритма является одним из основных понятий современ­ной математики и информатики, но зародилось оно еще в глубокой древности. Еще на ранних ступенях развития математики (Древний Египет, Вавилон и Греция) в ней стали возникать различные вычислительные процессы чисто механического характера, с помощью которых искомые величины могли быть вычислены последовательно из исходных величин по определенным правилам и инструкциям. Со временем процессы такого рода стали называть алгоритмами.

Термин алгоритм происходит от имени средневекового узбекского математика Аль Хорезми (IX в.), который сформулировал правила выполнения четырех арифметических действий в десятичной системе счисления. Процесс выпол­нения арифметических действий был назван алгоризмом.

С середины ХVIII в. термин алгоризм трансформировался в алго­рисмус, и его смысл состоял в комбинировании четырех арифметических операций. К середине ХХ в. стали употреблять термин алгорифм (от англ. algorithm), замененный позже в русском языке на алгоритм. При этом первоначально смысл данного термина чаще всего связывался с алгорифмами Евклида (древнегреч. математика) – процессами нахождения наибольшего общего делителя двух натуральных чисел, наибольшей общей меры двух отрезков и т.д.

Позже под алгоритмом стали понимать конечную последователь­ность точно сформулированных правил, которые позволяют решать те или иные классы задач. Данное определения не является строгим, т.к. неясно, что следует понимать под классом задач и под правилами их решения.

В современной информатике используется следующее определение алгоритма. Алгоритмом называют систему четких однозначных указаний, которые определяют последовательность действий над некоторыми объектами и после конечного числа шагов приводят к получению требуемого ре­зультата.

Алгоритмы, в которых решение поставленной задачи сводится к вы­полнению арифметических действий, называются численными. Алгоритмы, в которых решение поставленной задачи сводится к вы­полнению логических действий, называются логическими.

2.2. Свойства алгоритма

Любой алгоритм должен обладать следующими пятью свойствами:

1. Дискретность алгоритма предполагает, что решение задачи (т.е. алгоритм) разбито на отдельные шаги (операции, команды) и переход к сле­дующему шагу возможен только после выполнения предыдущего.

2. Определенность (точность) алгоритма предполагает, что каждая его команда должна однозначно определять действие исполнителя алгоритма (записанные в алгоритме команды должны иметь однозначную трактовку).

3. Понятность алгоритма подразумевает, что он должен включать в себя только те шаги или команды, которые понятны исполнителю (в алгоритме не мо­гут присутствовать команды, смысл которых неизвестен исполнителю).

4. Результативность (конечность) предполагает, что алгоритм дол­жен быть нацелен на получение конечного результата, т.е. исполнение алго­ритма должно закончиться за конечное число шагов.

5. Массовость алгоритма подразумевает, что алгоритм должен быть пригоден для решения целого класса однотипных задач (а не только для одной конкретной задачи).

2.3. Основные этапы решения задачи с помощью ЭВМ

Процесс составления алгоритма решения некоторой задачи принято называть алгоритмизацией этой задачи. В целом же процесс решения задачи с помощью ЭВМ в случае, когда невозможно применить для ее решения готовые про­граммные средства, состоит из следующих этапов:

1. Четкая формулировка задачи на профессиональном языке соответ­ствующей прикладной области знаний. При этом должно быть четко опреде­лено, какие данные будут считаться исходными, а также какие данные и в ка­кой форме должны быть получены в качестве результатов решения задачи.

2. Формальная математическая постановка задачи, т.е. представление ее в виде математических уравнений, соотношений, ограничений и т.п. Неко­торые задачи не требуют математической постановки, тогда данный этап может отсутствовать.

3. Выбор метода решения, который зависит от решаемой задачи, а также требований, предъявляемых к алгоритму и программе. Например, требований по быстродействию, объему памяти, точности вычислений.

Важность данного этапа определяется тем, что от выбора правильного метода в конечном итоге будет зависеть эффективность программы и качест­во получаемых результатов. Поэтому разработчик алгоритма должен иметь некоторый кругозор относительно возможных методов решения поставлен­ной задачи, чтобы выбрать из них наиболее приемлемый.

4. Разработка алгоритма, в процессе которой желательно рассмотреть несколько возможных вариантов и выбрать наилучший. При разработке ал­горитмов сложных задач может использоваться метод пошаговой детализа­ции.

5. Выбор структуры данных таким образом, чтобы используемая структура данных была наиболее естественной для решаемой задачи.

Так как от способа представления данных напрямую зависит способ их обработки, то этот этап тесно связан с предыдущим и может меняться с ним местами (структура данных может быть определена до разработки алго­ритма).

6. Программирование, т.е. запись алгоритма решения задачи в виде программы на каком-либо алгоритмическом языке.

В некоторых случаях желательно, чтобы предполагаемый к использо­ванию язык программирования (ЯП) был определен изначально (по крайней мере до разработки алгоритма и выбора структур данных). Это связано с тем, разные ЯП обладают разными возможностями (преимуществами и недостат­ками) по использованию различных структур данных, их обработке и т.д.

7. Тестирование и отладка программы, т.е. проверка правильности ее работы и исправление обнаруженных ошибок. В качестве тестов могут ис­пользоваться специально подобранные наборы исходных данных, для кото­рых заранее известны правильные результаты решения данной задачи.

2.4. Способы записи алгоритмов

Один и тот же алгоритм может быть записан разными способами. Их существует несколько, но основными являются следующие:

1. Словесный способ, т.е. описание алгоритма на естественном языке (словами).

2. Формульно-словесный способ, в котором кроме слов могут исполь­зоваться математические формулы.

3. Графический способ, т.е. в виде блок-схемы.

4. Программный способ, т.е. в виде программы на алгоритмическом языке.

2.5. Основные элементы блок-схемы

Запись алгоритма графическим способом, т.е. с помощью блок-схемы, является наиболее наглядным способом записи алгоритма, позволяющим легко «читать» даже сложные по структуре алгоритмы. Каждый пункт алгоритма отображается на схеме некоторой геометрической фигурой – блоком, который дополняется элементами словесной записи.

Блоки на схемах соединяются линиями потоков информации (в виде линий со стрелкой на конце). Основное направление потока информации идет сверху вниз и слева направо (тогда стрелки могут не указываться), снизу вверх и справа налево – в этих случаях стрелки обязательны. Количество входящих линий для блока не ограничено. Выходящая линия должна быть одна (кроме логического блока – блока принятия решения).

Таблица 2.

N	Элемент	Название элемента
		Блок начала или конца алгоритма
		Блок расчета (Вычислительный блок)
		Блок ввода или вывода данных
		Логический блок (Блок принятия решения)
		Блок модификации (Блок цикла с заданным числом повторений)

Существует специальный ГОСТ 19.002 – 80 (единая система программной документации), который регламентирует правила выполнения схем алгоритмов (форму блоков, толщину и размер линий, расстояние между блоками и т.п.). Эти правилам должны строго следовать профессиональные разработчики алгоритмов и программисты при создании блок-схем. В таблице 2 приведены пять из восьми основных элементов блок-схемы, которые будут использоваться при решении учебных задач.

2.6. Типовые структуры алгоритмов

Типовой (или базовой) структурой называют определенный набор блоков и стандартных способов их соединения для выполнения типичных последовательностей действий. В структурном программировании различают три типовых структуры: 1) линейную, 2) разветвляющуюся, 3) циклическую.

1. Линейная структура алгоритма, называемая также последовательной, предполагает, что действия (блоки) выполняются последовательно друг за другом в порядке их записи (следования). В блок-схеме алгоритма линейной структуры могут использоваться только блоки двух типов (не считая блоков начала и конца, которые должны быть у любого алгоритма): блоки расчета и блоки ввода/вывода (рис. 2).

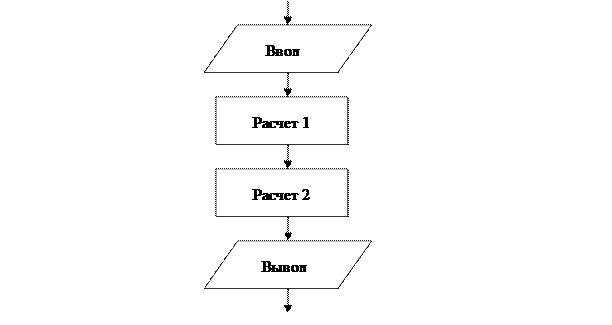Рис.2. Пример блок-схемы алгоритма линейной структуры

2. Разветвляющаяся структура алгоритма предполагает использование логического блока (блока принятия решения), в котором записывается некоторое условие для проверки. Данный блок имеет два выхода, один из которых помечается словом «Да» (или знаком «+»), другой – словом «Нет» (или знаком «–»).

Условие должно являться выражением логического типа, которое может принимать только одно из двух значений: истина или ложь (true или false). Если при проверке условия оно оказалось истинным, то далее выполнение алгоритма осуществляется по ветке «Да». В противном случае (если условие ложно) выполнение алгоритма происходит по ветке «Нет» (рис.3). Кроме обычного разветвления может использоваться его частный случай, называемый «обход», когда никаких действий на ветку «Нет» не задано (рис.4).

Рис.3. Разветвление Рис.4. Обход

3. Циклическая структура алгоритма предполагает многократное повторение некоторой последовательности действий («цикл» означает «повтор»). Однако «многократно» не значит «бесконечно». Организация цикла, никогда не приводящего к остановке выполнения алгоритма, является нарушением требования его результативности – получения результата за конечное число шагов (см. свойства алгоритма в пункте 2.2).

Любой цикл состоит из двух компонент: 1) условия цикла, которое должно проверяться на каждом шаге цикла и определять момент завершения работы цикла (т.е. выход из цикла), 2) тела цикла, представляющего собой последовательность действий, подлежащих многократному повторению. В зависимости от порядка записи этих компонент различают 2 типа циклов: 1) цикл «с предусловием» (рис. 5), 2) цикл «с постусловием» (рис. 6).

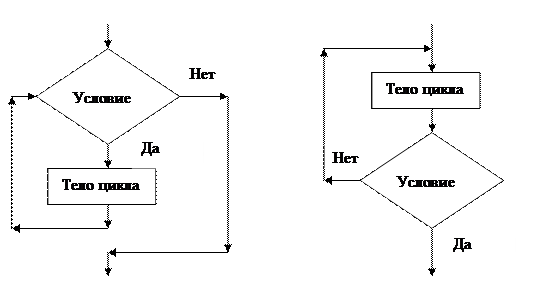
Рис.5. Цикл «с предусловием» Рис.6. Цикл «с постусловием»

По количеству повторений тела цикла различают также 2 типа циклов: 1) цикл с незаданным числом шагов (повторений), 2) цикл с заданным числом шагов.

Особенность цикла с заданным числом шагов в том, что условие цикла в нем не задается в явном виде, а как бы подразумевается. Управление цикла осуществляется через специальную управляющую переменную (как правило, целого типа). В заголовке цикла вместо условия записываются параметры этой управляющей переменной: ее начальное и конечное значения, а также шаг изменения (по умолчанию используется шаг равный 1). Таким образом, через параметры управляющей переменной в заголовке цикла уже задается определенное количество повторений тела цикла.

Для оформления цикла с заданным числом повторений в блок-схеме используется специальный блок модификации (см. таблицу 2 в пункте 2.5). Для записи такого цикла в программе на языках Бейсик и Паскаль используется оператор For. Синтаксис этого оператора в языке VBA описан далее в пункте 3.4 (Глава 3).

В рассмотренном ниже примере (рис. 7) изображен цикл, который всегда (т.е. независимо от действий, заданных до цикла, исходных параметров задачи и содержания тела цикла) будет работать 50 раз. На первом шаге цикла тело выполнится при i=1, на втором шаге – при i=3, на третьем шаге – при i=5 и т.д. Последний раз тело цикла будет выполнено при i=99.

Рис.7. Пример блок-схемы цикла с заданным число повторений

где i – управляющая переменная,1 – ее начальное значение,

100 – конечное значение, 2 – шаг изменения значения i.

В языке VBA можно использовать операторы цикла различного синтаксиса. Основные операторы VBA рассмотрены далее в пункте 3.4 (Глава 3), в том числе синтаксис двух операторов цикла: For – для цикла с заданным числом повторений, While – для цикла с незаданным числом повторений.

2.7. Стандартные алгоритмы

Стандартными называют алгоритмы, эффективные способы организации которых уже были разработаны ранее (т.е. уже известны). К стандартным алгоритмам относятся алгоритмы решения таких задач как накопление суммы и произведения элементов массива, поиск максимального и минимального элемента массива, сортировка элементов массива.

2.7.1. Алгоритм накопления суммы (произведения)

Суть алгоритма накопления в том, что сумма или произведение вычисляются не сразу, а постепенно накапливаются за счет добавления очередного элемента массива на каждом шаге цикла. Для правильной работы алгоритма переменной, в которой будет накапливаться сумма (произведение), должно быть присвоено определенное начальное значение, не влияющее на действие накопления. Например, при накоплении суммы в качестве начального значения берется 0 (т.к. прибавление нуля не влияет на сумму), а при накоплении произведения начальное значение равно 1 (при умножении на 1 произведение не меняется).

Пусть Х – одномерный массив из n элементов (чисел). Требуется вычислить сумму элементов массива S. Переменную-индекс для перебора элементов в цикле обозначим как i.

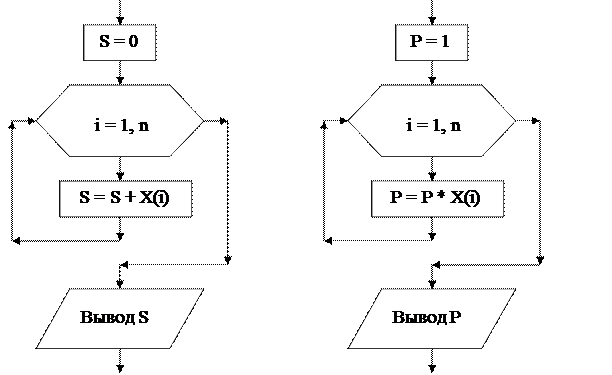
Рис. 8. Накопление суммы Рис. 9. Накопление произведения

Блок-схема накопления суммы элементов массива Х в переменную S изображена на рисунке 8. Накопление произведения элементов массива Х в переменную P выполняется аналогично накоплению суммы (рис. 9).

2.7.2. Алгоритм поиска максимального (минимального) элемента

Поиск максимального или минимального элемента массива основан на последовательном переборе всех элементов массива и сравнении каждого элемента с некоторой переменной, в которую должен быть найден максимум (минимум). Если значение элемента превышает значение этой переменной, то оно заносится в нее. При поиске минимума проверяется обратное условие.

Для правильной работы алгоритма переменной для поиска максимума (минимума) должно быть присвоено некоторое начальное значение до цикла поиска. Это должно быть значение, не превышающее максимального элемента (или не меньше минимального элемента). Поэтому в качестве начального значения в обоих случаях может быть взят любой элемент массива (даже если он сам будет максимумом или минимумом, то он не больше и не меньше самого себя). Для простоты в качестве начального значения при поиске максимума (минимума) берут первый элемент массива.

Пусть Х – одномерный массив из n элементов (чисел), М – переменная для поиска максимального (минимального) элемента, k – номер максимального (минимального) элемента, i – номер очередного элемента.

Блок-схема поиска максимального элемента массива и его номера изображена на рисунке 10. Поиск минимального элемента выполняется аналогично, только необходимо поменять знак сравнения “>” на “<” при проверке условия в цикле.

Рис. 10. Поиск максимального элемента и его номера

2.7.3. Алгоритмы сортировки

Сортировкой называют упорядочивание элементов по какому-либо признаку. Например, числовые данные можно упорядочить (отсортировать) либо по возрастанию, либо по убыванию их значений. А строковые данные – в алфавитном порядке, либо в порядке обратном алфавитному.

Наиболее известны два метода сортировки: 1) сортировка методом выбора, 2) пузырьковая сортировка.

2.7.3.1. Метод выбора

Данный метод сортировки базируется на поиске минимального (максимального) элемента. Вначале находится минимальный элемент, который затем меняется местами с первым элементом. Далее находится следующий минимум, т.е. начиная со второго элемента. Затем найденный минимум меняется со вторым элементом и т.д.

Таким образом, упорядочивание осуществляется за счет постепенной расстановки элементов по своим местам через последовательный выбор очередного минимума. Сортировка по убыванию выполняется аналогично, только поиск минимальных элементов заменяется на поиск максимальных элементов.

Пусть Х – одномерный массив из n элементов (чисел). Требуется отсортировать его по возрастанию значений элементов. Для реализации метода выбора потребуется организовать два цикла: один вложенный в другой. Поэтому потребуется два индекса: переменная i – для управления внешним циклом, переменная j – для управления внутренним циклом. Переменная М используется для поиска минимального (максимального) элемента. Необходима также дополнительная переменная А для обмена местами очередного минимума (максимума) с нужным элементом. В переменную k заносится номер очередного минимума (максимума).

На рисунке 11 изображена блок-схема сортировки по возрастанию элементов массива Х методом выбора.

Сортировка по убыванию выполняется аналогично, только необходимо заменить знак «<» на знак «>» (чтобы заменить поиск минимумов на поиск максимумов).

Рис. 11. Сортировка по возрастанию методом выбора

2.7.3.2. Пузырьковая сортировка

Суть данного метода сортировки в том, что осуществляется последовательный перебор пар соседних элементов массива и сравнение этих элементов между собой (первого и второго, второго и третьего и т.д.). Если предыдущий элемент в паре окажется больше последующего, то они меняются местами. Однократного перебора и сравнения всех пар от начала до конца массива может быть недостаточно для окончательного выполнения сортировки. Поэтому в общем случае требуется выполнять перебор и сравнение пар «соседей» не один раз, а многократно. Если же при переборе и сравнении всех пар не будет сделано ни одной перестановки, то это будет признаком окончания сортировки (каждый предыдущий элемент не больше последующего).

Таким образом, будет получена сортировка по возрастанию. Для сортировки по убыванию требуется проверять обратное условие и делать перестановку элементов, если в паре последующий элемент больше предыдущего.

Пусть Х – одномерный массив из n элементов (чисел). Требуется отсортировать его по возрастанию значений элементов. Для реализации пузырьковой сортировки потребуется организовать два цикла: один вложенный в другой. Во внутреннем цикле (с управляющей переменной i) будет осуществляться сравнение пар соседних элементов X(i) и X(i+1) от начала и до конца массива. Для перестановки соседних элементов потребуется дополнительная переменная А. Во внешнем цикле будет проверяться условие окончания сортировки (по значению переменной-признака). В качестве переменной-признака окончания сортировки можно использовать либо переменную, логического типа (со значениями True и False), либо целочисленную переменную (со значениями 0 и 1). Будем использовать переменную В целого типа. Если при проверке условия В=0, то сортировка еще не завершена. Если В=1, то сортировка закончена.

Рис.12. Пузырьковая сортировка по возрастанию

На рисунке 12 изображена блок-схема сортировки по возрастанию элементов массива Х методом пузырьковой сортировки.

Сортировка по убыванию выполняется аналогично, только необходимо заменить знак «<» на знак «>» при сравнении соседних элементов.

Контрольные вопросы

1. Что такое алгоритм?

2. Какими свойствами должен обладать алгоритм?

3. Что называют алгоритмизацией?

4. Какие основные этапы решения задачи с помощью ЭВМ?

5. Какие существуют способы записи алгоритма?

6. Как выглядят основные элементы блок-схемы?

7. Что называют типовой структурой алгоритма?

8. Какие элементы не могут присутствовать в блок-схеме алгоритма линейной структуры?

9. Чем обход отличается от ветвления?

10. Что такое цикл?

11. Как отличить разветвляющуюся структуру от циклической?

12. Какие типы циклов различают?

13. Какие алгоритмы называют стандартными?

14. В чем суть алгоритма накопления?

15. Как работает алгоритм поиска максимума (минимума)?

16. В чем суть алгоритма сортировки методом выбора?

17. В чем суть алгоритма сортировки методом пузырька?

Дата добавления: 2014-10-17; просмотров: 654; Нарушение авторских прав

Мы поможем в написании ваших работ!